汽车控制臂路试载荷谱的编制与转化

朱雪冰，魏志刚，张李侠（.安徽工业大学机械工程学院，安徽马鞍山4303；.奇瑞汽车股份有限公司实验和整车技术研究院，安徽芜湖4009）

汽车控制臂路试载荷谱的编制与转化

朱雪冰1，魏志刚1，张李侠2
（1.安徽工业大学机械工程学院，安徽马鞍山243032；2.奇瑞汽车股份有限公司实验和整车技术研究院，安徽芜湖241009）

提出1种多工况下普通轿车悬置零件程序载荷谱的编制方法，并对球销载荷与衬套载荷之间转化关系进行研究。基于试验测得控制臂球销道路载荷谱，运用雨流计数法将随机载荷谱进行处理；通过统计法建立多路况下载荷均幅值的复合概率密度函数，编制出1个完整循环下的程序载荷谱；运用非线性方程将球销载荷谱转化为衬套载荷谱。实现了汽车悬置零件的多工况道路程序载荷谱的编制及载荷之间的转化，该方法可为路试载荷下零样疲劳寿命预测及疲劳寿命试验提供参考。

多路况；控制臂；载荷谱

汽车控制臂中的零件在车辆行驶过程中由于路面不平整而承受来自悬架的冲击力。冲击载荷是随机发生、不规则的，其中载荷的幅值和循环次数是零件产生疲劳破坏的主要因素［1］。因此，在对零件进行疲劳寿命预测之前，须对零件的载荷谱进行编制。与随机载荷谱相比，程序载荷谱形式简单且更符合实际情况，在预测寿命时可大大节省计算时间。

目前，有关载荷谱在特种装备、机械、航空等领域中的研究取得了一些成果［2-5］。汤清洪等［6］以自行火炮为研究对象，针对扭力轴二维载荷的非对称特点，对非对称型载荷的编制方法进行了阐述；谭援强等［7］以混凝土运输车搅拌桶减速器为例，对传统单级设计载荷的方法进行改进，提出确定多级设计载荷的方法；闫楚良等［8］研究了飞机高置信度中值载荷谱编制原理和方法。但对于多工况下普通轿车悬置零件程序载荷谱的编制，由于其复杂性，国内外相关文献较少。汽车控制臂中某些悬置零件（如衬套）体积较小、空间有限，致使采集载荷谱时无法直接获取，给悬置零件的疲劳寿命预测增添了难度。基于此，文中以汽车控制臂为研究对象，运用数理统计法将多工况道路随机载荷谱编制成一维程序载荷谱，并利用非线性方程将球销载荷谱转化为衬套载荷谱，为悬置零件疲劳寿命计算提供参考。

1　控制臂球销随机载荷谱的获取

载荷谱是对悬置零件（如衬套）耐久性疲劳寿命预测的关键，准确获取各路况下载荷谱是衬套疲劳寿命预测的首要条件。衬套较小、空间有限，因此在路谱采集时将传感器布置在控制臂总成另外一侧的球销上，控制臂总成模型如图1。衬套的整车试验在4种代表性的路况下进行，路况具体为综合路况1、综合路况2、绕8字爬坡、比利时路，这4种路况按照规定的行使顺序及比例组成一个子循环，再由4个子循环构成一个完整的路试循环。

采用布置在控制臂总成另外一侧球销上的传感器分别测得整车x向及y向在4种路况下的随机载荷谱。由于工作环境的影响，测得的载荷时间历程信号中存在大量的干扰信号，在分析处理信号前须对其进行滤波去噪及剔除异常峰值［9］。图2为初步处理后综合路况1下的随机载荷谱。由图2可以看出，初步处理后的随机载荷谱仍十分复杂，且不规则，须对其进行进一步处理。

图1　控制臂总成模型Fig.1 Control arm assembly model

图2　初步处理后的综合路况1下随机载荷谱Fig.2 Random load spectrum of the comprehensive road 1

2　程序载荷谱的编制

整车y向载荷对衬套疲劳寿命影响较小，文中不作阐述，只对4种路况下整车x向随机载荷谱进行编制处理。

2.1载荷谱的雨流计数处理

使零件产生疲劳破坏的主要因素是载荷的幅值和循环次数［1］，因此需引入疲劳循环次数记数法对随机载荷谱进行计数处理。雨流计数法［9］是其中应用较多的一种计数法，该方法不仅将复杂的载荷转化为有限个完整的全循环或半循环，同时考虑循环载荷应变特性。对图2（a）中的随机载荷谱进行雨流计数处理得到载荷均幅值三维柱状图，如图3所示。

2.2载荷分布规律及检验

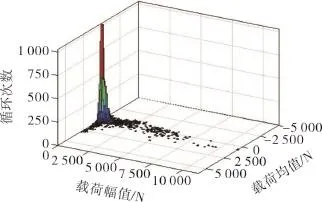
图3　载荷均幅值三维柱状图Fig.3 Three-dimensional histogram of the road amplitude and mean

根据载荷均幅值的分布规律建立载荷均幅值的联合密度函数，但在建立联合密度函数之前应对载荷均幅值进行独立性检验。利用Matlab对样本数据进行计算得到4种路况下2个随机变量之间的相关系数，如表1。根据表1可知载荷均幅值是弱相关的，表明载荷均值、幅值是相互独立的。

图4　正态分布概率图Fig.4 Graph of normal distribution probability

图5　双参数威布尔分布概率图Fig.5 Graph of two parameter Weibull probability

根据载荷均幅值相互独立，得到载荷均幅值的联合概率密度函数表达式

表1　各路况载荷谱均幅值之间相关系数Tab.1 Correlation coefficient between the amplitude of the various load spectra

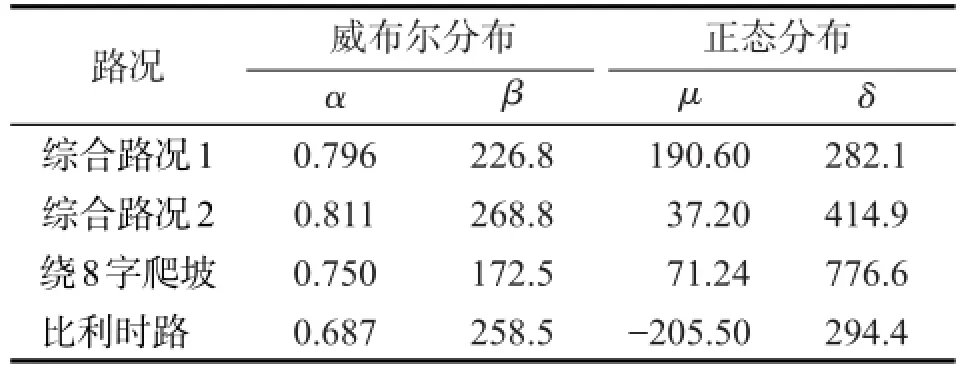
表2　各工况参数值Tab.2 Each working condition parameter value

2.3载荷均幅值二维谱的编制

衬套整车试验场地是固定的，每种工况采集的载荷子样波动不大，根据雨流统计结果可知1个完整试验循环下载荷累积频次为1 063 920，满足工程上编谱的要求［10］。进行衬套整车试验时一个完整循环中每种路况有其特定的行驶循环次数，各路况载荷循环次数的加权系数为

式中：Ni为第i路况下的载荷循环次数；N为1个完整试验循环载荷出现的总循环次数。根据各路况载荷循环次数的加权系数可求出4种路况合成后的复合概率密度函数［6，11］

由于载荷均值服从正态分布，载荷幅值服从双参数威布尔分布，且相互独立，由式（4）求各路况载荷均幅值的最大值。

GC条件：进样口温度25 ℃，载气He，流速1.2 mL/min。进样量1 μL，分流进样，分流比40：1。色谱柱为DB-WAX (30 m×0.25 mm×0.25 μm)，升温程序40 ℃恒温2 min，以5 ℃/min的升温速度升至180 ℃，然后以15 ℃/min的升温速度升至230 ℃，保持5 min。MS条件：EI电离子源，电子能量70 eV，离子源温度 200 ℃，接口温度 250 ℃。扫描范围 33.00～350.00 u。

式中：P=1/扩展后频次；UP可从标准正态分布表中查出。由文献［6］可知编谱时取各路况载荷均值的最大值为最大载荷均值，载荷幅值的最大值为最大载荷幅值，根据计算求得幅值最大值x′max=6 378.5N，均值最大值-x′max=3 527.1N。程序载荷谱均幅值一般分为8级，均值按照等间距法进行分级［12］，其等间距τ可由式（5）求出

其中κ为幅值比值系数。二维载荷谱中各级均幅值循环次数Nij由式（7）得出。

式中：ai+1，ai分别表示载荷幅值积分上、下限；bj+1，bj为载荷均值积分上、下限。其中ai=（xi-1+xi）/2，i，j=2，3，…，8。由式（7）计算得到对应载荷均幅值的各级循环次数Nij，形成8×8的二维载荷谱，如表3所示。

表3　1个完整试验循环下球销的二维载荷谱Tab.3 Two dimensional load spectrum of ball pin under a complete test cycle

2.4一维程序载荷谱编制

文中采用波动中心法将二维载荷谱转化为一维程序载荷谱，忽略均值对零部件疲劳寿命的影响，只保留载荷变程与累积频次的关系［4］。首先需求出每级幅值对应的波动中心［12］，求取方法如式（8）。

式中：Si表示第i级幅值对应的波动中心；sj为第j级均值；nij为第i级幅值第j级均值累积频次。表4为1个完整试验循环下一维程序载荷谱，表中的各级载荷幅值仍延用二维谱中的幅值分级，频次则取二维谱中载荷幅值对应的各级载荷均值频次之和。

表4　1个完整试验循环下的一维程序载荷谱Tab.4 One-dimensional program load spectrum under a complete cyclic test

3　球销载荷与衬套载荷之间的转化

为使衬套寿命预测结果更为准确，需知衬套直接承受的载荷状态，因此将球销载荷转化为衬套载荷。如图6所示，假定控制臂前后衬套内圈固定，A 和B分别为2个衬套的外圈中心。

将控制臂总成看作为一个刚体，由力和力矩平衡可得：

其中：Fx，Fy分别为控制臂在球销中心处承受整车x向和y向的载荷；RAx（ΔxA），RBx（ΔxB）分别为A和B处受到的整车x向支反力，是位移Δx的函数；RAy（ΔyA），RBy（ΔyB）分别为A和B处的整车y向支反力，是位移Δy的函数；Δ是前衬套中心点与球销中心在两衬套中心投影点的距离。假设控制臂总成为刚性运动，且整车z轴扭转角度很小，因此文中忽略扭转的影响。

橡胶为非线性形变，故A和B点的支反力与位移为非线性关系。通过试验测衬套整车坐标系下x，y方向的刚度曲线，分别用多项式和指数函数进行拟合，拟合结果如图7。由图7可以看出，后衬套的整车x向和y向刚度用指数函数拟合效果较好，前衬套方向刚度曲线用一次函数进行拟合也获得了较好的结果。

经参数拟合得到衬套刚度函数为：

联合式（9），（10），运用1stOpt软件对非线性方程组求解，得到衬套整车方向的位移并代入刚度函数式中便求出衬套的受力状态，表5为由球销载荷转化为衬套载荷的一维载荷谱。

图6　控制臂受力分析Fig.6 Control arm stress analysis

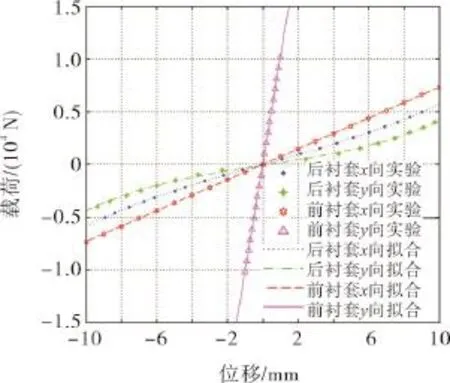
图7　衬套刚度拟合曲线Fig.7 Fitting curves of bushing stiffness

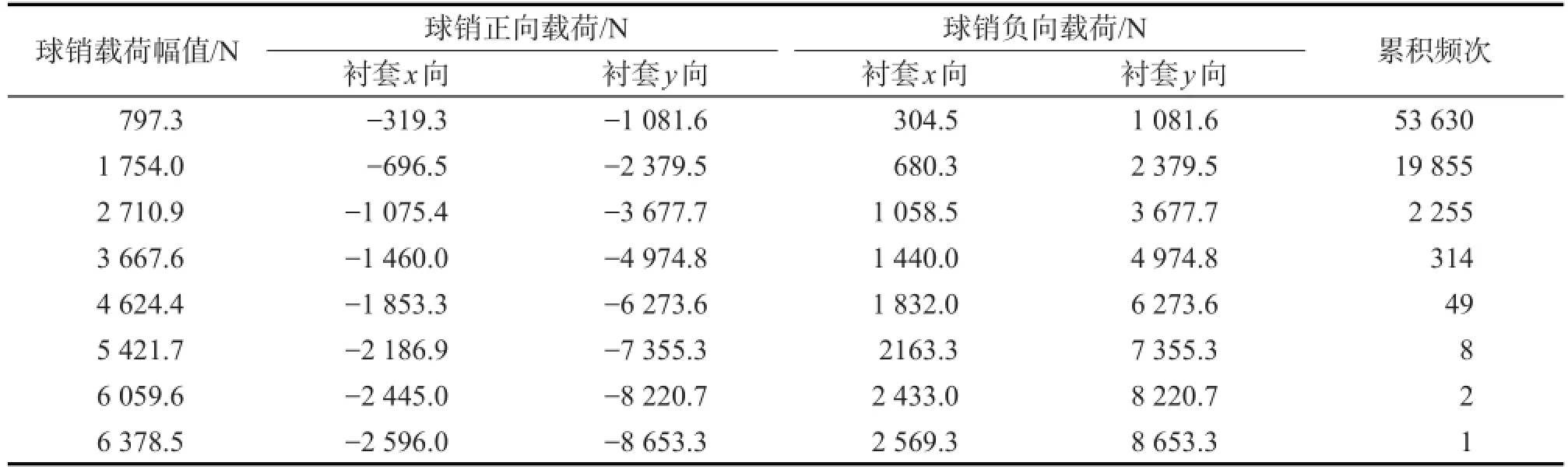
表5　转化后的一维载荷谱Tab.5 One-dimensional load spectrum after transformation

由表5可以看出，当球销只受到整车x向载荷时衬套则同时受到x，y2个方向的力，且同正同负。

5　结　论

以汽车控制臂为研究对象，应用统计分析理论将衬套整车试验测得的控制臂球销处的随机荷谱编制成简单的一维程序载荷谱，并利用非线性求解法将球销载荷谱转化为衬套载荷谱，为橡胶衬套在路试工况下的疲劳寿命计算奠定了基础。文中载荷谱的编制与转化方法对其他多路况下零件载荷谱的编制有一定的参考价值。

［1］姚斌辉.基于载荷谱的橡胶悬置疲劳预测与实验研究［D］.广州：华南理工大学，2012:37-38.

［2］童靳于，潘紫薇，包家汉，等.基于ANSYS的扭力杆装置疲劳寿命分析［J］.安徽工业大学学报（自然科学版），2013，30（4）:426-429.

［3］SONSINO C M.Fatigue testing under variable amplitude loading［J］.International Journal of Fatigue，2007，29（6）:1080-1089.

［4］LAUE S，BOMAS H.Spectrum fatigue life assessment of notched specimens based on the initiation of short cracks［J］.International Journal of Fatigue，2006，28（9）:1011-1021.

［5］JOHANNESSON P，SVENSSON T.Fatigue life prediction based on variable amplitude tests-methodology［J］.International Journal of Fatigue，2005，27（8）:954-965.

［6］汤清洪，马吉胜，贾长治.扭力轴多工况二维随机疲劳载荷谱的编制［J］.振动与冲击，2007，26（2）:105-107.

［7］谭援强，左晃，张跃春，等.多级多工况传动载荷处理方法及应用［J］.机械强度，2011，33（6）:932-938.

［8］闫楚良，高镇同.飞机高置信度中值随机疲劳载荷谱的编制原理［J］.航空学报，2000，21（2）:118-123.

［9］贾海波.轮式装载机传动系统载荷谱测试与编制方法研究［D］.长春：吉林大学，2009:43-47.

［10］高云凯，徐成民，方建光.车身台架疲劳试验程序载荷谱研究［J］.机械工程学报，2014，50（4）:92-98.

［11］郝晋峰，石全，史宪铭，等.机械零件疲劳载荷谱的编制方法研究［J］.机械与电子，2009（1）:76-78.

［12］张英爽，王国强，王继新，等.工程车辆传动系载荷谱编制方法［J］.农业工程学报，2011，27（4）:179-183.

［13］陈东升，项昌乐，陈欣.军用车辆传动系零件载荷谱的建立［J］.机械强度，2002，24（2）:310-314.

责任编辑：何莉

Preparation and Transformation of the Road Test Load Spectrum of Automobile ControlArm

ZHU Xuebing1，WEI Zhigang1，ZHANG Lixia2
（1.School of Mechanical Engineering，Anhui University of Technology，Ma'anshan 243002，China；2.Chery Automobile Co.Ltd.，Institute of Experimental and Vehicle Technology，Wuhu 241009，China）

A method for preparing the road load spectrum of the vehicle suspension parts under multiple working conditions was proposed，and the transformation relationship between the bushing load and the load of the ball pin was studied.Based on the experimental test，the load spectrum of the ball pin road was measured，and the random load spectrum was processed with rain flow counting method.The composite probability density function of the load amplitude under multiple working conditions was established by using the mathematical statistics method，and the programmed load spectrum of a complete cycle was compiled.The load spectrum of the ball pin was converted into the bushing load spectrum by using nonlinear equation.The preparation and transformation of the load spectrum of multiple working conditions for vehicle suspension parts are realized.The method can provide reference for fatigue life prediction and fatigue life test of specimen based on test load.

multiple road conditions；control arm；load spectrum

U463

A

10.3969/j.issn.1671-7872.2016.01.013

1671-7872（2016）-01-0058-06

2015-09-25

安徽工业大学研究生创新研究基金项目（2014045）

朱雪冰（1990-），女，安徽宿州人，硕士生，主要研究方向为有限元建模及仿真。

魏志刚（1975-）男，山东潍坊人，博士，副教授，主要研究方向为有限元建模和仿真。