关于马氏链遍历性的一个注记

2016-08-02孙成恩范爱华安徽工业大学数理科学与工程学院安徽马鞍山243032

安徽工业大学学报（自然科学版） 2016年1期

关键词：马氏爱华范数

程成，孙成恩，范爱华（安徽工业大学数理科学与工程学院，安徽马鞍山243032）

关于马氏链遍历性的一个注记

程成，孙成恩，范爱华
（安徽工业大学数理科学与工程学院，安徽马鞍山243032）

引入定义在σ-有限可测空间（S，ℱ，μ）中随机核与范数的概念，通过采用随机转移核密度｛｝pn（x，y）n∈ℕ替换离散型非齐次马氏链中转移矩阵的方法，得到状态连续非齐次马氏链遍历性的充分必要条件。所得结论进一步完善了非齐次马氏链的遍历性质。

非齐次马氏链；随机核；Cauchy收敛；Lebesgue控制收敛定理

随机稳定性是探究马氏链性质的重要内容之一，对于随机稳定性的研究主要从马氏过程的不可约性、常返性以及马氏链的遍历性入手。Isaacson在文献［1-2］中分别讨论了可数状态非齐次马氏链的遍历性及其几何遍历的特征，在文献［3］中系统地总结非齐次马氏链的遍历性并给出了若干公开问题，Pitman在文献［4］中研究马氏链转移收敛的一致速度。Neumann等在文献［5］中探索出矩阵列乘积的某些收敛性，并将该结论应用到非齐次马氏链的遍历性中。Isaacson等在文献［6］中利用光谱条件研究了马氏链的强遍历性与收敛速率。Coppersmith等在文献［7］中指出非齐次马氏链弱遍历的条件。Prieto-Rumeau等分别在文献［8］和文献［9］中讨论了连续时间马氏链的一致遍历和强遍历行为。此外，汪进在文献［10］中总结了m重非齐次马氏链的遍历性。本文在上述文献的基础上，给出连续状态马尔可夫链满足遍历性的充分必要条件。

1　基本假设

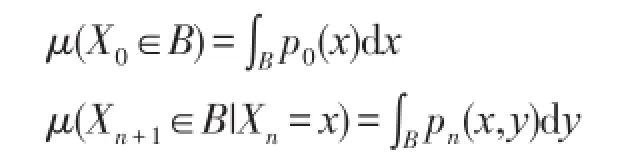
并且对任意的m，n∈ℕ，有

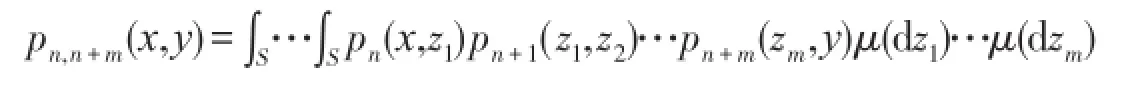
定义1设K（x，y）是定义在S×S上的任意可积核，称

为K的范数。对任意2个随机核K和L，由KL（x，y）=∫K（x，z）L（z，y）μ（dz）定义其乘积KL。

定义2设p（x，y）是随机转移核，称

为随机转移核的Dobrushin系数。为方便起见，令δ（P）=1-α（P）。关于δ（P）以及范数的基本性质，可参见文献［1］。

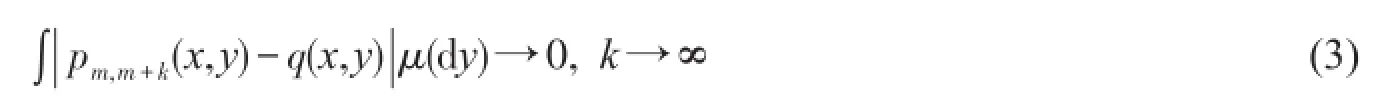
2　主要结论

注此处的定义类似于Cauchy收敛条件，但x不能恒等于z，故条件不能放宽成x=z。证明必要性

由于

充分性

令x=z，则pm，m+k（x，y）依k为Cauchy序列，所以pm，m+k（x，y）→qm（x，y），k→∞。根据Fatou引理得

故

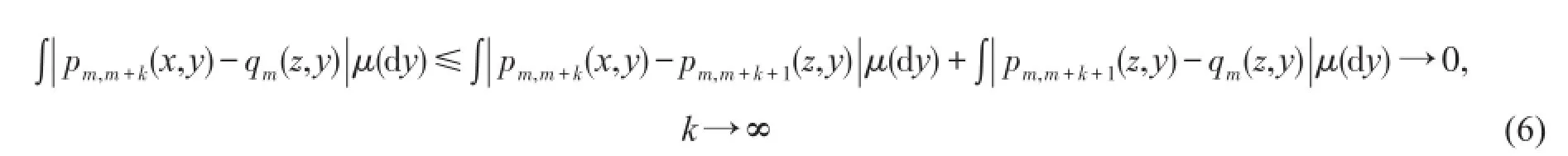
因此

又

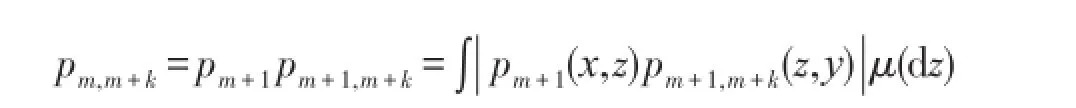
令k→∞，利用Lebesgue控制收敛定理可得

根据Fatou引理知q（y）≥0且∫q（y）μ（dy）≤1。又因为故为概率密度。证毕。

［1］ISAACSON D.Ergodicity for countable inhomogeneous Markov chains［J］.LinearAlgebra and itsApplications，1982，48:37-44.

［2］ISAACSON D.Acharacterization of geometric ergodicity［J］.Probability Theory&Related Fields，1978，49（3）:267-273.

［3］ISAACSON D L，MADSEN R W.Markov Chains:Theory andApplications［M］.New York:Wiley，1976:249-251.

［4］PITMAN J W.Uniform rates of convergence for Markov chain transition probabilities［J］.Probability Theory&Related Fields，1974，29（3）:193-227.

［5］NEUMANN M，SCHNEIDER H.The convergence of general products of matrices and the weak ergodicity of Markov chains［J］. LinearAlgebra and itsApplications，1999，287（1）:307-314.

［6］ISAACSON D，LUECKE G R.Strongly ergodic Markov chains and rates of convergence using spectral conditions［J］.Stochastic Processes and theirApplications，1978，7（1）:113-121.

［7］COPPERSMITH D，WU C W.Conditions for weak ergodicity of inhomogeneous Markov chains［J］.Statistics&Probability Letters，2008，78（17）:3082-3085.

［8］PRIETO-RUMEAU T，HEMÁNDEZ-LERMA O.Uniform ergodicity of continuous-time controlled Markov chains:A survey and new results［J］.Annals of Operations Research，2012:1-45.

［9］SCOTT M，ISAACSON D.Strong ergodicity for continuous-time，non-homogeneous Markov chains［J］.Journal of Applied Probability，1982，19（3）:692-694.

［10］汪进.m重非齐次马氏链的遍历性［J］.安徽工业大学学报（自然科学版），2006，23（2）:227-231.

［11］MADSEN R W，ISAACSON D L.Strong ergodic behavior for non-stationary Markov processes［J］.Annals of Probability，1973，1（2）:329-335.

［12］SENETA E.Inhomogeneous Markov chains and ergodicity coefficients:John Hajnal（1924—2008）［J］.Communications in Statistics-theory and Methods，2014，43（7）:1296-1308.

责任编辑：丁吉海

ANote on the Ergodicity of Markov Chains

CHENG Cheng，SUN Cheng'en，FANAihua
（School of Mathematics Physics Science and Engineering，Anhui University of Technology，Ma′anshan 243032，China）