聚能射流参数的工程化函数研究*

丁亮亮,李翔宇,卢芳云,李振铎

(国防科学技术大学理学院,长沙　410073)



聚能射流参数的工程化函数研究*

丁亮亮,李翔宇,卢芳云,李振铎

(国防科学技术大学理学院,长沙410073)

摘要:为了分析药型罩锥角、壁厚及炸药参数对聚能射流性能的影响规律,利用AUTODYN对射流形成过程及参数进行了数值模拟。结果表明,射流头部速度随锥角及壁厚的增加而减小,随炸药爆速的增加而增加;射流半径随药型罩壁厚和锥角的增加而增加。并拟合得到了射流头部速度和射流半径的工程化函数,利用该工程化函数可以快速估算聚能射流的性能参数。

关键词:射流速度;射流半径;壁厚;锥角;量纲分析

0引言

破甲战斗部是依靠聚能装药在爆炸后通过爆轰波将释放出的能量传递给金属药型罩,使得金属药型罩快速向轴线压合,进而产生金属射流来达到破甲的作用效果,其在军用领域和民用领域有着广泛的应用。通过研究药型罩结构参数及炸药参数对金属射流的影响,对于破甲战斗部的设计具有一定的指导意义。

关于聚能射流的形成过程及性能,国内外专家学者已做了大量的研究。Birkhoff等人(1948年)首先系统地阐述了聚能射流形成理论,即Birkhoff定常理论;Pugh、Eichelberger和Rostoker(1952年)对定常理论作了重要改进,提出了非定常射流形成理论,即PER理论[1]。Allison、Vitali等人通过实验证实了PER理论的有效性[2],德国的Held研究了锥角对射流形状和速度的影响[3],韩世峰等人研究了结构参数对射流的影响[4],张会锁等人研究了药型罩锥角和壁厚对射流的影响[5-6],姚志华等人研究了药型罩锥角和壁厚对EFP的影响[7]。

1射流参数影响规律分析

聚能射流对目标的毁伤效果主要通过破甲深度和开坑口径两个指标来衡量,根据侵彻流体力学理论可以得到影响射流侵彻性能公式[8]:

(1)

(2)

式中:H为射流的破甲深度;Vj为射流头部速度;Vs为射流尾部速度;tp为射流断裂前持续时间;ρt为靶板密度;ρj为射流密度;R为最大开坑半径;rj为射流半径;Pt为靶板强度。

由式(1)和式(2)可知,影响射流侵彻性能的因素主要包括:射流速度、射流半径、射流密度以及靶板的密度和强度。在药型罩材料和靶板材料确定情况下,影响因素退化为射流速度和射流半径。

文中以射流头部速度和射流半径为研究对象,基

于量纲分析原理研究分析射流头部速度和射流半径与药型罩锥角、壁厚、锥底口径等因素之间的关系,并通过AUTODYN仿真软件获得大量的仿真实验数据,最终得到影响射流头部速度和射流半径的工程化函数。

2数值计算模型

2.1有限元模型

由于聚能装药结构模型具有轴对称特性,为了提高计算速度、节约计算空间,在建模时采用二维轴对称模型来分析药型罩锥角和壁厚对射流性能的影响,有限元模型如图1所示,主要包括炸药、壳体、药型罩及空气4个部分。

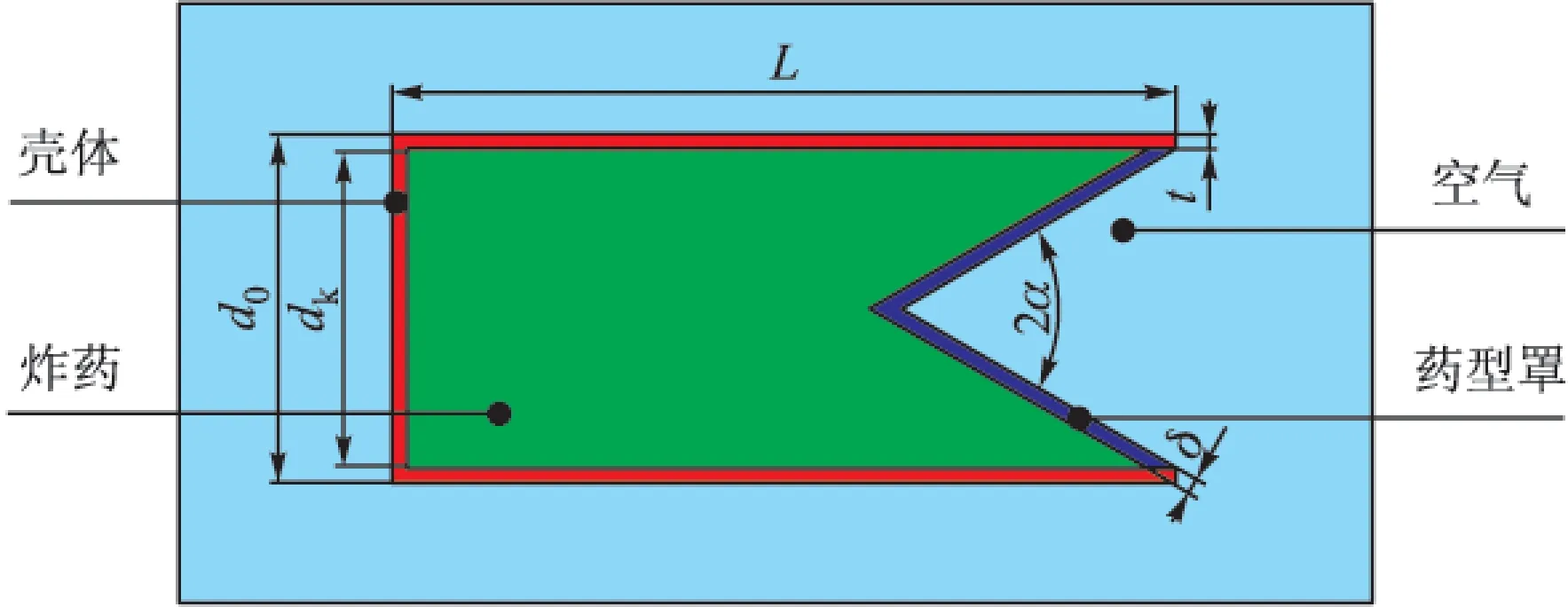
图1　有限元模型

参考文献由[9]可知:当药型罩材料为铜时,药型罩厚度的取值范围为δ=(0.03～0.04)dk。设定壳体的外径为60 mm,则模型的结构参数如表1所示。 由[10-11]可知,射流半径与药型罩锥底半径的平方根成正比。于是有a=b=1/2,则上式可化为:

表1　结构参数 mm

2.2材料模型及参数

计算模型包括壳体、药型罩、炸药和空气域。材料参数和材料模型取自Autodyn自带的数据库,各部分的材料模型如表2所示。

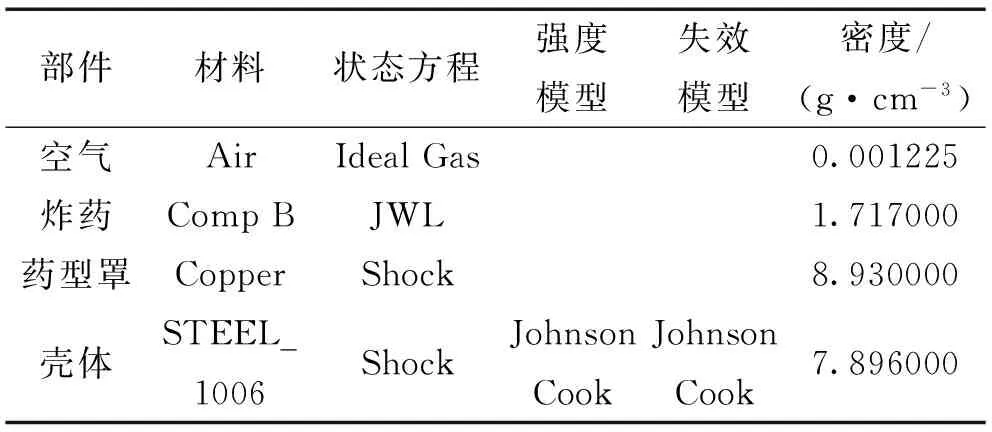
表2　材料模型及参数

2.3算法及接触

空气域采用Euler网格,为了保证数值计算的精度,在网格划分时采用中心区域加密的渐变网格。壳体、药型罩和炸药采用Lagrange网格,而后将炸药和药型罩Euler网格替换。定义Lagrange网格与Euler网格之间的接触为Automatic,定义起爆方式为线起爆模拟。

2.4计算工况

壳体材料、装药类型、起爆方式、药型罩材料、壁厚及锥角等因素均影响射流性能。文中主要从药型罩的壁厚及锥角两个参数来研究药型罩结构对形成射流的性能进行规律分析。数值模拟过程中选取30组不同工况,即在不同壁厚(1.0 mm,1.5 mm,2.0 mm,2.5 mm,3.0 mm)条件下分别选取药型罩锥角为45°,50°,55°,60°,65°,70°进行数值模拟。

3射流头部速度的工程化函数

根据上文的理论分析以及参考文献[10]可知,在分析射流头部速度Vj的影响因素时,主要考虑以下因素:炸药爆速D、药型罩半锥角α、药型罩壁厚δ、药型罩锥底口径dk。于是有如下函数关系:

(3)

根据量纲独立原则,选取D和dk为独立量纲物理量,因此式(3)可改写为:

(4)

于是可以假定:

(5)

根据数值模拟的数据结果,得到射流头部速度与炸药爆速比值Vj/D和药型罩壁厚与锥底口径比值δ/dk之间的关系如图2所示。

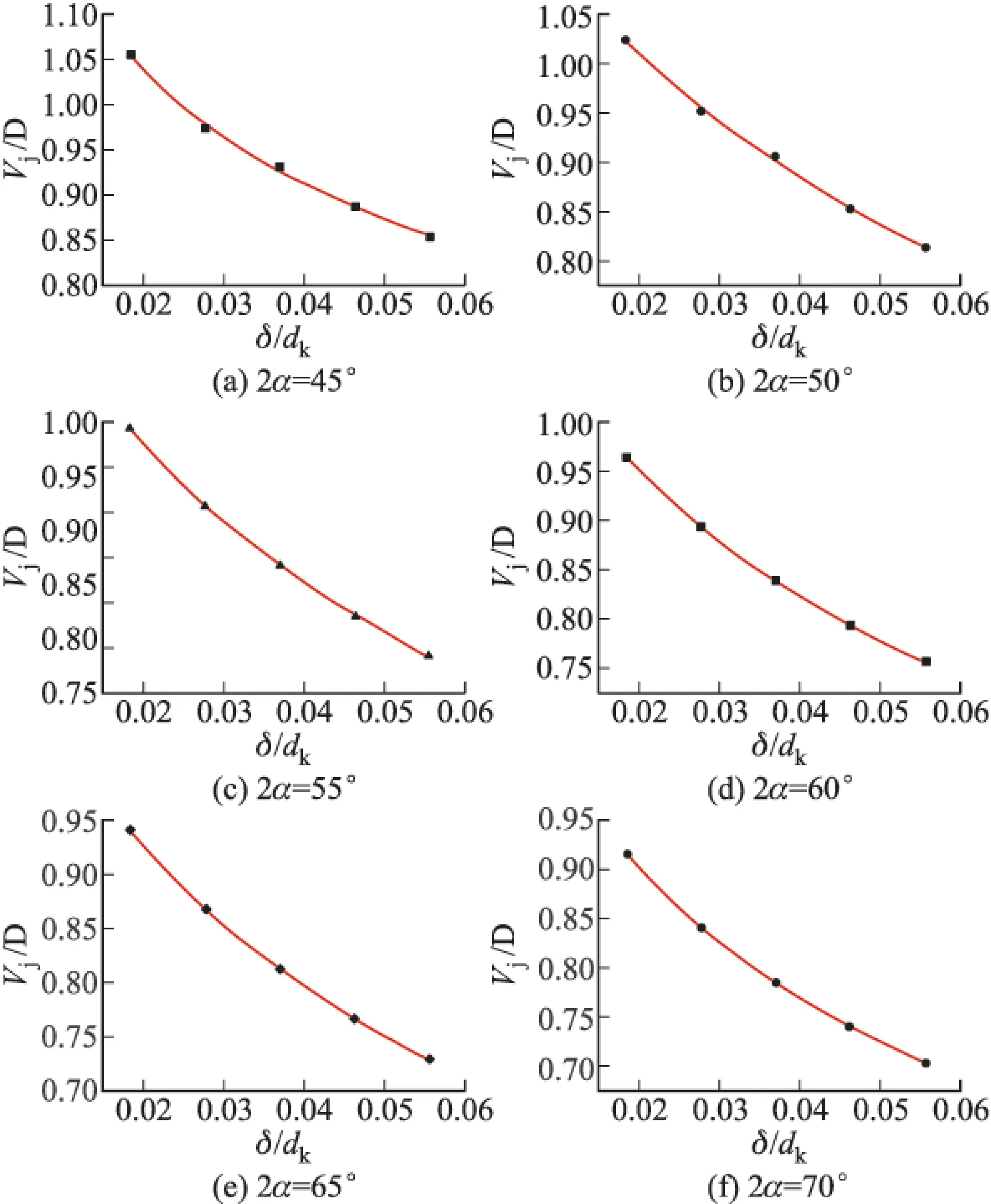
图2　Vj/D与δ/dk之间的关系

对Vj/D与δ/dk之间的关系在不同α下进行拟合,得到各曲线的拟合公式及相关参量如表3所示。

表3　Vj/D与δ/dk关系曲线的拟合公式及相关参量

由表3可知,c0值近似为常数,取c0=-0.191。并且得到c1f(α)与α之间的关系曲线如图3所示。

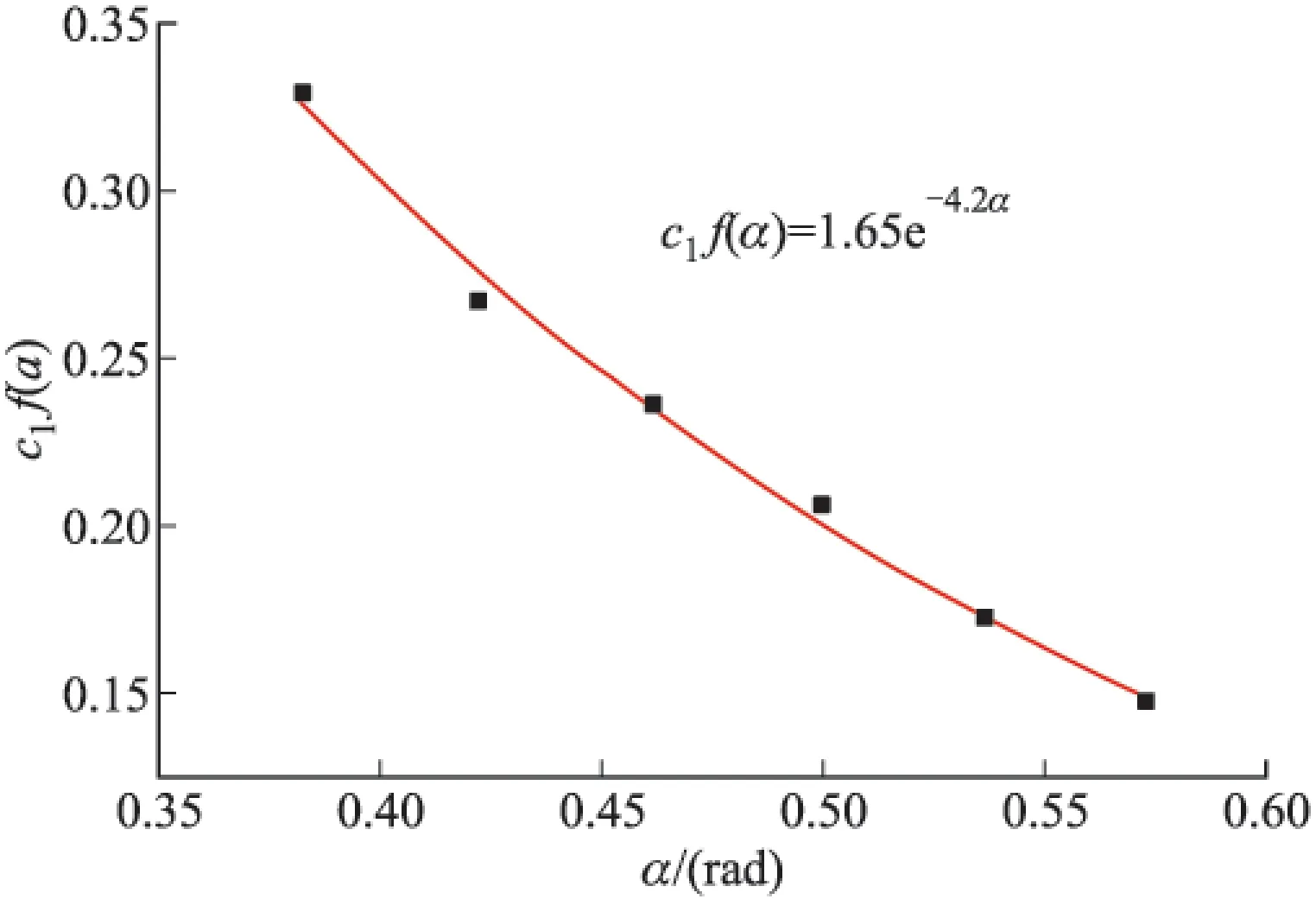
图3　c1f(α)与α之间的关系曲线

可得到射流头部速度Vj与炸药爆速D、壁厚δ、半锥角α、锥底口径dk之间的工程化函数为:

(6)

当药型罩半锥角α趋于0°时,药型罩锥底口径dk也趋于0,此时有关系:Vj=1.65D。

由式(6)可知:Vj/D与δ/dk呈对数关系,与药型罩半锥角α呈指数关系。当其他条件一定时,射流头部速度随着药型罩锥角及壁厚的增加而减小,随着炸药爆速的增加而增加。

为了验证式(6)的合理性,选取了锥角为60°,壁厚为2.0 mm,锥底口径为54 mm,壳体厚度为3.0 mm条件下的五组不同爆速炸药进行数值模拟,对比分析结果如表4所示。

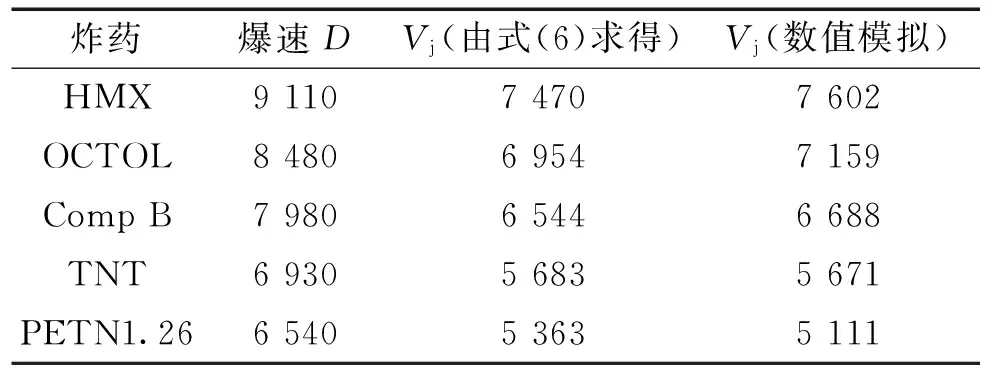
表4　5组不同爆速炸药的对比分析　m/s

由此可以看出,数值模拟得到的试验结果与理论分析结果基本一致,并且通过5组不同爆速炸药对比分析了由公式推导和数值模拟得到的射流头部速度,发现式(6)可以较好的吻合。

4射流半径的工程化函数

分析了5种不同类型的炸药对射流半径的影响,结果如图4所示,可见炸药爆速对射流半径的影响可不予以考虑。

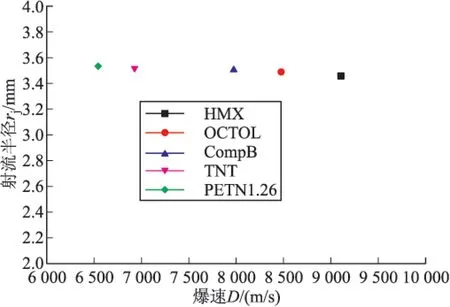
图4　炸药爆速对射流半径的影响

在分析药型罩结构对射流半径rj的影响时,主要考虑药型罩半锥角α、药型罩壁厚δ、锥底半径rd等参数对射流的影响。于是有如下函数关系:

(7)

根据量纲齐次的原则,可假定:

(8)

式中:a+b=1,c=const,C0=const。

(9)

由数值模拟得到的数据点,可以得到射流半径rj与药型罩半锥角正弦值之间的关系如图5所示。

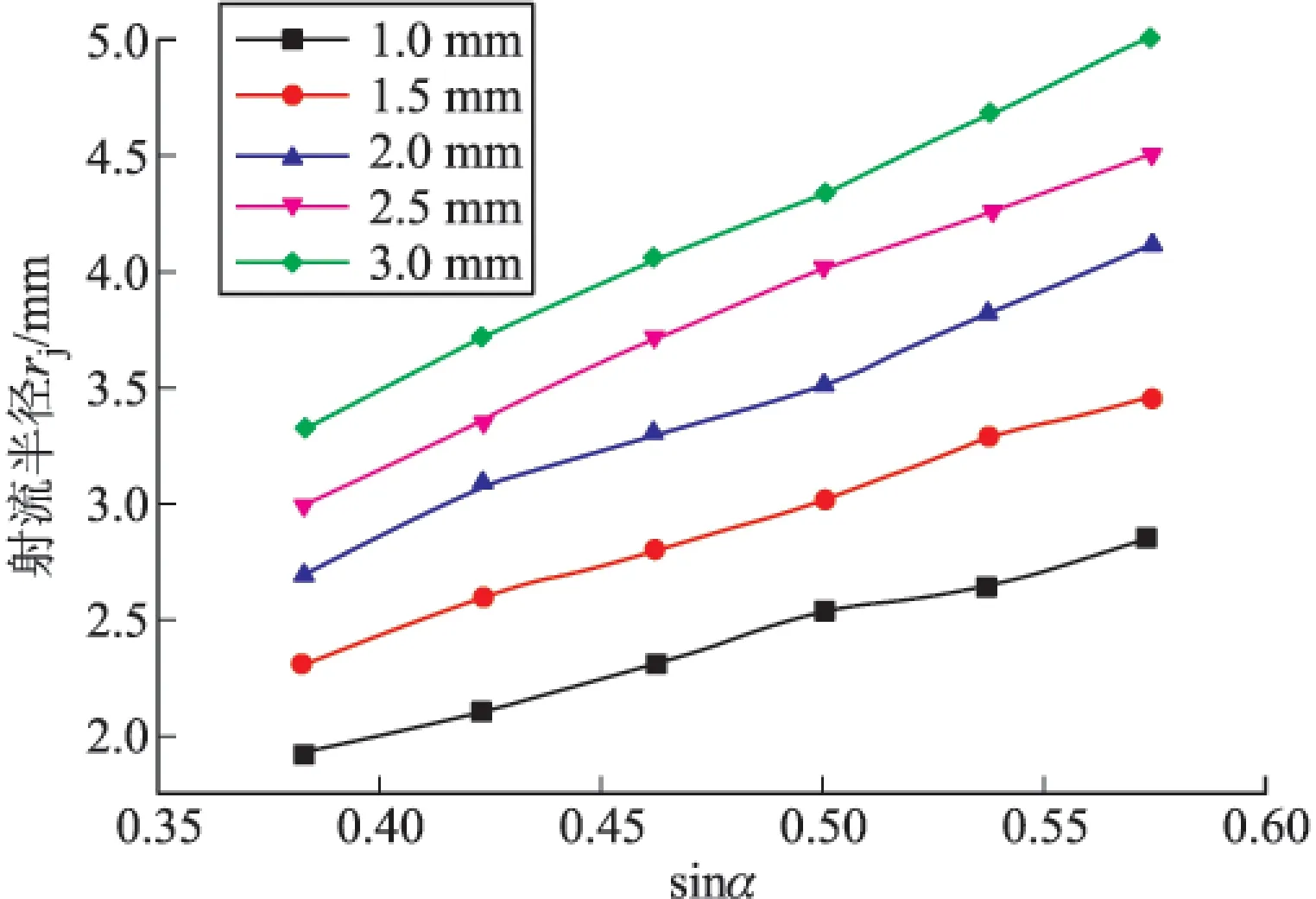
图5　射流半径rj与sinα之间的关系

对射流半径rj与sinα的关系曲线进行拟合,可以得到各曲线的拟合公式及相关参量如表5所示。

由图5可知,射流半径rj与sinα之间近似呈线性关系,即c=1。若忽略较小的常数项,可得到射流半径与药型罩锥角、壁厚以及锥底半径之间的工程化函数为:

(10)

式中:K为常数,一般取K=1.05。

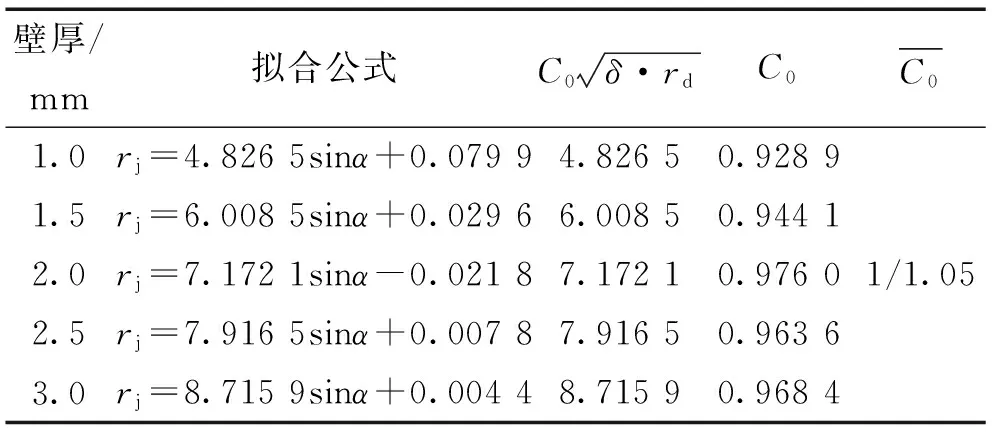
表5　rj与sinα关系曲线的拟合公式及相关参量

由式(10)可知,射流半径随着药型罩壁厚的增加而增加,随着药型罩锥角的增加而增加,并且与参考文献[10]中的分析结果很好的吻合。

5结论

利用AUTODYN对射流头部速度和半径进行了数值模拟,考察了炸药爆速D、药型罩半锥角α、药型罩壁厚δ、药型罩锥底口径dk或锥底半径rd等因素对射流参数的影响,结合量纲分析理论获得了射流参数的工程化函数,形成的结论如下:

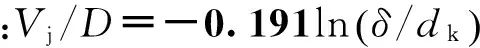
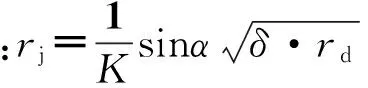
3)在工程应用中,可利用得到的工程化函数来快速估算聚能射流的性能参数,进而为破甲战斗部的威力设计提供参考。

[1]PUGH E M, EICHELBERGER R J, ROSTOKER N. Theory of jet formation by charges with lined conical cavities [J]. Journal of Applied Physics, 1952, 23(5): 532-536.

[2]ALLISON R E, VITALI R. An application of the jet formation theory to a 105 mm shaped charge: BRL-1165 [R].

1962.

[3]WALTERS W P, ZUKAS J A. Fundamentals of shaped charges [M].New York John Wiley & Sona. Inc.,1989: 51-82.

[4]韩世锋, 张国伟, 陈振华, 等. 结构参数对成型装药射流影响的数值仿真 [J]. 机电技术, 2014(5): 34-35.

[5]张会锁, 赵捍东, 王芳, 等. 药型罩锥角对聚能射流影响的数值模拟 [J]. 弹箭与制导学报, 2005, 25(4): 351-353.

[6]张会锁, 赵捍东, 王芳，等. 药型罩壁厚对聚能射流影响的数值模拟 [J]. 测井技术, 2006, 30(1): 47-49.

[7]姚志华, 王志军, 王辉, 等. 锥角和壁厚对对多爆炸成型影响的数值模拟 [J]. 弹箭与制导学报, 2007, 27(2): 155-157.

[8]吴成, 廖莎莎, 孙韬, 等. 钨合金药型罩材料的大破孔聚能战斗部研究 [J]. 北京理工大学学报, 2009, 29(9): 760-762.

[9]赵文宣. 弹丸设计原理 [M]. 北京: 北京工业学院出版社, 1988: 198-199.

[10]隋树元, 王树山. 终点效应学 [M]. 北京: 国防工业出版社, 2000: 201-210.

[11]崔卫超, 王志军, 吴国东, 等. 不同锥角和楔角对锥形和线形聚能装药射流的影响 [J]. 弹箭与制导学报, 2011, 31(4): 85-88.

*收稿日期:2015-04-28

基金项目:国家自然科学基金(11202237)资助

作者简介:丁亮亮(1993-),男,河南南阳人,硕士研究生,研究方向:高效毁伤战斗部技术。

中图分类号:TJ410.1

文献标志码:A

Study on Engineering Function of Parameters of Jet

DING Liangliang,LI Xiangyu,LU Fangyun,LI Zhenduo

(College of Science, National University of Defense Technology, Changsha 410073, China)

Abstract:In order to analyze jet parameters affected by cone angle, liner thickness and explosive parameters, formation characteristic parameters were simulated by AUTODYN nonlinear dynamics analysis software. The results show that the head velocity of jet increases with the increase of liner thickness, cone angle and explosive detonation velocity, jet radius decreases with the decrease of liner thickness and cone angle. In addition, engineering functions of the head velocity of jet and the liner thickness were got for quickly estimating parameters of jet.

Keywords:jet velocity; jet radius; thickness; cone angle; dimensional analysis