环壳过渡对潜艇锥-锥连接结构强度和稳定性的影响
2020-06-29荆腾吴梵张二张宇晨
荆腾,吴梵,张二,张宇晨
海军工程大学舰船与海洋学院,湖北武汉430033
0 引 言
潜艇耐压壳体的直径会因内部布置的变化而改变,其艏、艉部常采用截头的圆锥壳,当锥壳与柱壳连接后,壳体母线在连接处存在折角,使得该区域附近产生了很大的纵向弯矩和纵向弯曲应力。在纵向弯曲应力作用下,壳中面环向应力不再是控制应力,而内表面的纵向应力远远超出了规范的许用值[1],使该部位成为了耐压壳体的一个薄弱环节。
针对上述问题,王安稳和郭日修[2]提出了锥-环-柱结合壳结构形式,此结构在两段母线存在折角的锥壳和柱壳之间采用圆环壳过渡形式,从根本上解决了结合处壳体子午线切线处倾角不连续的问题,且以较小的重量代价大幅度降低锥-柱结合部的应力峰值,是一种值得推广的连接结构形式。目前,针对锥-环-柱结构形式的力学性能分析和模型试验都已开展了较多研究。白雪飞等[3-4]运用传递矩阵方法,建立了旋转壳单元的场传递矩阵,推导了肋骨和母线倾角不连续位置的点传递函数,利用得出的传递矩阵对潜艇耐压壳体锥-环-柱结构进行了强度和稳定性计算。吕岩松等[5-6]采用分区样条等参元法对潜艇加肋凸、凹锥-环-柱结合壳进行了分析,结果表明,以满足强度要求为前提且保持环壳半径与柱壳半径比值相同时,环壳壳板需要的厚度随着半锥角的增大而增大。吴梵等[7]采用分区样条等参元法,研究了各项结构参数对加肋凹型锥-环-柱结合壳应力和稳定性的影响,并认为采用环壳连接结构能有效降低锥-柱结合部的纵向弯曲应力,但对于降低环向应力效果有限。张二等[8-10]分析了锥-环-柱结合壳加工过程中的初始几何缺陷,运用仿真方法分析了不同工况下不同尺寸的初始缺陷对锥-环-柱典型结合部应力、稳定性和极限承载能力的影响。肖文勇等[11]利用有限元方法对锥柱直接连接结构、厚板削斜结构、锥-环-柱结构分别进行了应力分析,通过比较,证实了锥-环-柱结构可大幅降低纵向弯曲应力的峰值,且结构质量较小,得到的锥-环-柱结构中环壳半径对结构力学性能的影响最大,其次是环壳厚度,最后是半锥角。毛开仁等[12-13]对加肋凹型锥-环-柱结合壳的破坏模式及其机理进行了研究,并对环壳中面应力在其破坏前卸载以及环壳两端肋骨的高应力现象作出了合理解释。
在潜艇结构实际设计过程中,会遇到2 个不同半锥角的圆锥壳相连接的情况。在2 个圆锥壳之间采用环壳连接可以使两侧锥壳的母线在连接处实现光顺过渡,此结构形式在以往的研究中鲜有涉及,故有必要对其进行力学性能方面的研究。本文将建立锥-锥及锥-环-锥连接结构的模型,运用有限元法对两种结构在不同锥角情况下过渡段典型应力、稳定性等情况进行分析对比以得到采用环壳过渡结构对锥-锥连接结构的力学性能的影响,为潜艇耐压结构设计提供参考。
1 有限元模型
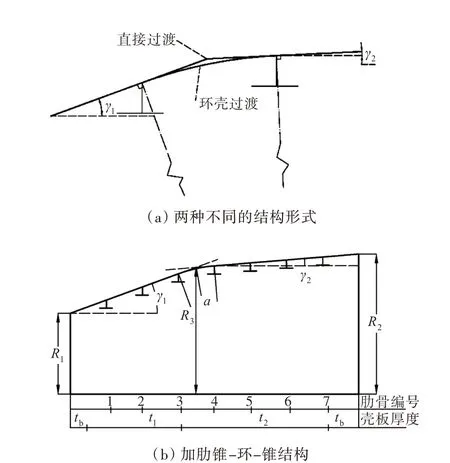
图1 两种过渡结构及加肋锥-环-锥结合壳结构示意图Fig.1 Two transition structure and structural diagrams of ring-stiffened cone-toroid-cone combined shell

图2 结构有限元模型Fig.2 Finite element model of structures
模型所受静水压力p=6.62 MPa,施加在耐压壳外表面。设定边界为固支,结构左侧边界仅放松轴向,同时将结构纵向力以(其中n 为该侧端面的节点数)的集中力形式按力的等效作用原理分配到左侧锥端面的各节点上。经过不断细分网格并多次计算,通过对比发现,当沿轴向和环向各划分64,144 个单元,总单元数为21 744、网格尺寸为100 mm×196 mm 时,计算结果已有较高的精度。
2 环壳过渡对结构过渡段典型应力的影响
通过计算发现,不同锥角的锥-锥结构过渡段中控制应力一般为过渡结构处的内表面纵向应力:当左侧锥角较小而右侧锥角较大时,控制应力为过渡处左、右两侧的锥壳跨中处的中面环向应力;锥-环-锥结构中的控制应力为环壳左、右侧锥壳跨中处的中面环向应力。假定潜艇锥壳半锥角γ1在10°~30°之间,表1~表3 分别为左侧γ1为10°,20°和30°时,不同右侧半锥角γ2的锥-锥结构和锥-环-锥结构过渡段内3 种典型应力的大小情况,其中过渡处在锥-环-锥结构中是指环壳段跨中处。
由表1~表3 对比发现,在不同的左侧锥角下,锥-锥或锥-环-锥结构典型应力随右侧锥角的变化规律一致。在右侧锥角较小时,锥-锥结构过渡处的内表面纵向应力为其控制应力,随着锥角的增大,过渡处内表面纵向应力不断减小,控制应力则变为过渡段左、右侧锥壳的中面环向应力。在采用环壳过渡后,过渡处内表面纵向应力大幅降低,环壳段左、右两侧锥壳的中面环向应力始终为结构过渡段内的控制应力,同时由于锥角的增大导致结构半径增大,当锥角增加的幅度足够大后,右侧锥壳跨中处中面环向应力将取代左侧锥壳跨中处中面环向应力成为结构过渡段的控制应力。
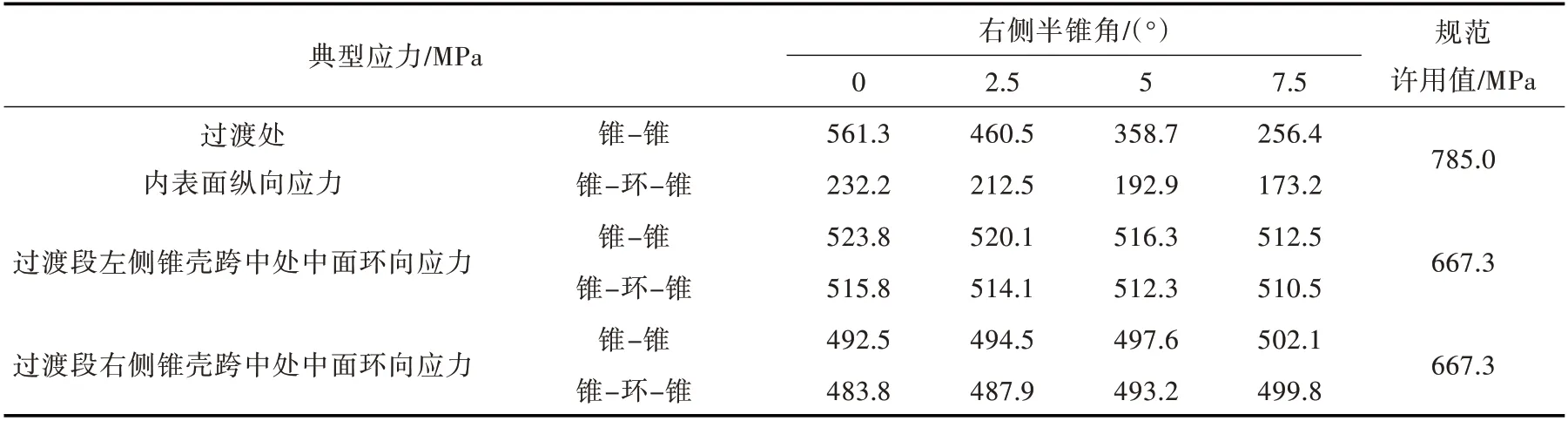
表1 左侧半锥角为10°时锥-锥、锥-环-锥结构过渡段的典型应力值Table 1 Typical stress values of transition section of cone-cone and cone-toroid-cone structures with left semi-cone angle of 10°
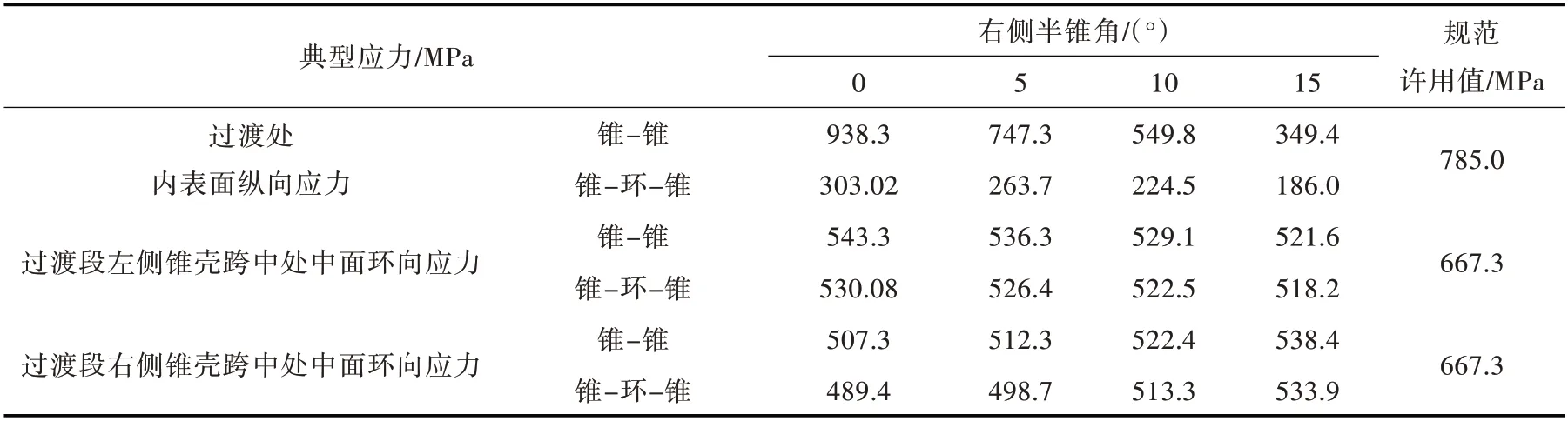
表2 左侧半锥角为20°时锥-锥、锥-环-锥结构过渡段的典型应力值Table 2 Typical stress values of transition section of cone-cone and cone-toroid-cone structures with left semi-cone angle of 20°

表3 左侧半锥角为30°时锥-锥、锥-环-锥结构过渡段的典型应力值Table 3 Typical stress values of transition section of cone-cone and cone-toroid-cone structures with left semi-cone angle of 30°
同时发现,当右侧锥角相同,左侧锥角越小,锥-锥结构的内表面纵向应力也越小。分析可知,当左、右两侧锥壳锥角间的差值越小,结合处母线的斜率变化越小,结构在过渡处产生的纵向弯矩和纵向应力就越小。当结构左、右侧两锥角间的差值小到一定范围内时,内表面纵向应力不再成为结构控制应力,此时使用环壳过渡将失去意义。
表4 和表5 分别统计了不同左、右锥角下锥-锥和锥-环-锥(含锥-柱与锥-环-柱)结构过渡处内表面纵向应力和峰值应力情况。由表4 可知,当左、右两锥角间的差值越大,过渡处内表面纵向应力越大,结构在过渡处的应力集中问题越突出,使用环壳过渡后结构过渡处内表面纵向应力下降的幅度就越大,环壳过渡对降低结构过渡处高纵向应力的作用也就越突出。由表5 可知,当左、右两侧锥角间的差值小于10°时,环壳过渡对降低结构过渡段控制应力的作用有限,采用环壳进行过渡的意义较小。
3 环壳过渡对舱段弹性和稳定性的影响
保持左侧锥角为20°不变,右侧锥角在0°~15°之间变化。建立整个舱段的有限元模型,其边界条件、载荷、网格尺寸均保持不变,得到不同右侧锥角下锥-环-锥与锥-锥结构舱段一阶弹性失稳模态,如图3~图5 所示。
由图3~图5 可知,两种结构的失稳模式都为肋间壳板的失稳,随着锥角的增加,失稳的区域会由过渡段左侧的锥壳过渡到右侧的圆锥壳上,并且同一失稳区域内弹性失稳压力与锥角之间呈线性关系。
当右侧锥角为0°时,采用环壳过渡对锥-锥结构的整体稳定性影响最大,锥-环-柱结构相比锥-柱结构舱段整体稳定性提高了2.25%。当锥角在8°以内时(图5),失稳区域发生在左侧锥壳,2 种结构形式的弹性失稳压力随锥角增加而增加,锥-环-锥结构舱段弹性失稳压力大于锥-锥结构,2 两者差值随锥角增加而不断减小;当锥角大于8.5°而失稳区域发生在右侧锥壳时,两种结构形式的弹性失稳压力随锥角的增加而减小,由于主要失稳变形区域集中在距离过渡段较远的锥壳段上,结构过渡形式对其影响较小,锥-环-锥结构的舱段弹性失稳压力与锥-锥结构保持一致。
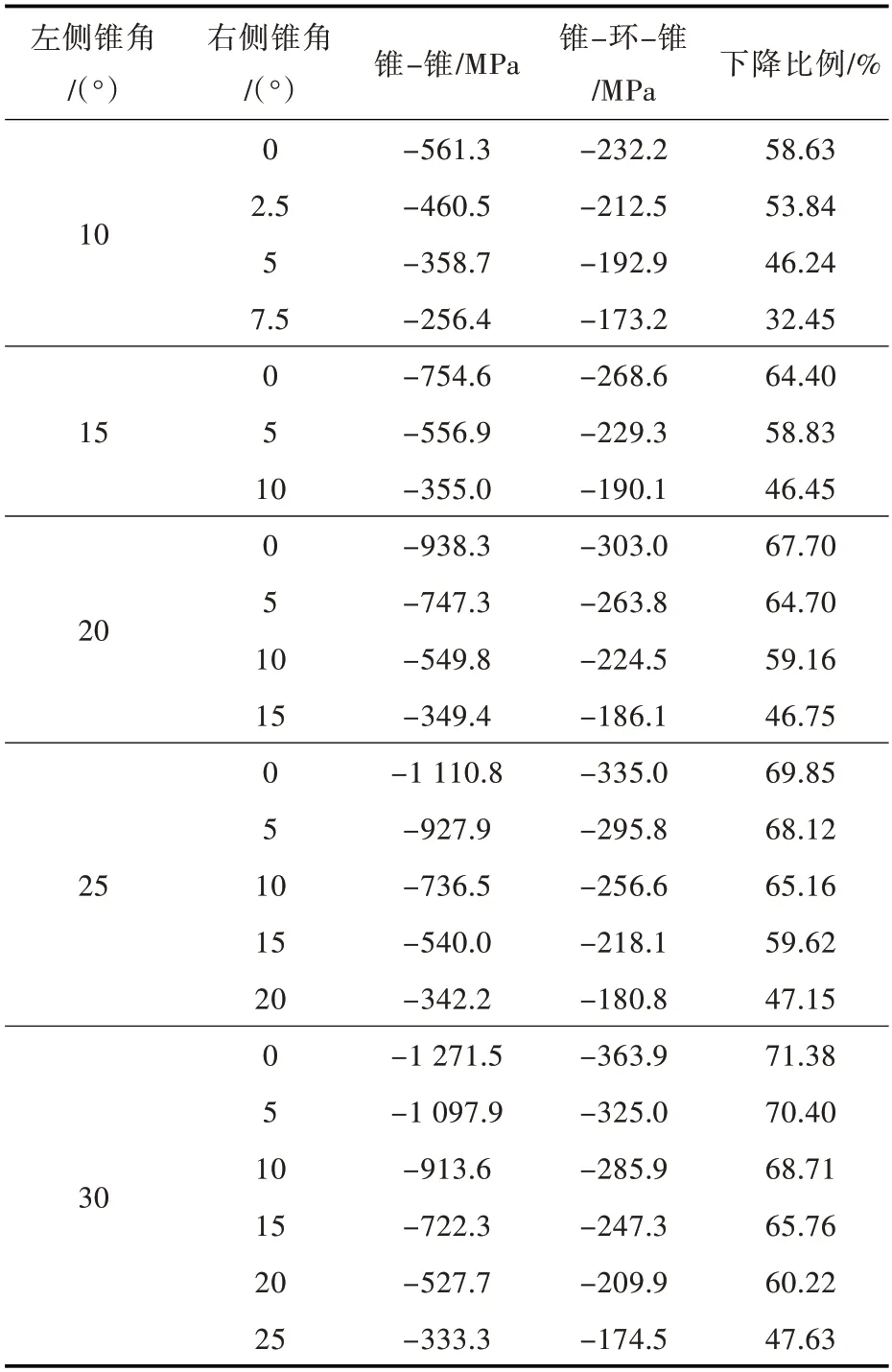
表4 不同锥角下锥-锥、锥-环-锥结合处内表面纵向应力值Table 4 Longitudinal stress values on the inner surface of cone-cone and cone-toroid-cone joints with different cone angles


图3 右侧锥角不同时锥-环-锥结构失稳变形云图Fig.3 Instability deformation contours of cone-toroid-cone structures with different right cone angles

图4 右侧锥角不同时,锥-锥结构失稳变形云图Fig.4 Instability deformation contours of cone-cone structures with different right cone angles

图5 结构舱段弹性失稳压力随右侧锥角的变化情况Fig.5 Change of elastic buckling pressure of structural compartment with right cone angle
4 结 语
本文采用数值仿真方法对不同锥角的锥-锥及锥-环-锥结构过渡段强度及舱段弹性稳定性进行了计算。结果表明:一定条件下使用环壳过渡对降低锥-锥结构过渡处应力峰值的作用显著;且锥-环-锥结构具有更加优异的力学性能。本文研究可为后续的物理模型试验提供参考。
