状态信息和轨道信息下的非合作目标精密跟踪技术*

黄　普,孙守明,李恒年

(宇航动力学国家重点实验室,西安　710043)



状态信息和轨道信息下的非合作目标精密跟踪技术*

黄普,孙守明,李恒年

(宇航动力学国家重点实验室,西安710043)

摘要:针对随机脉冲推力控制下的空间机动目标跟踪问题,提出一种基于状态信息和轨道信息的实时跟踪算法。该算法通过基于机动推力a-β动力学模型和改进当前统计模型的并行计算滤波器,完成空间非合作目标高精度实时跟踪。同时,利用直观的轨道信息,完成机动检测,采取重置滤波参数的方式获得更快的收敛速度和稳健性。仿真实验表明该算法可有效检测机动,实现了对非合作目标机动目标的轨道确定,具有一定的工程实用性。

关键词:状态信息和轨道信息;a-β动力学模型;改进当前统计模型

0引言

随着航天科技的进步,空间攻防对抗与预警任务成为趋势,如何利用观测信息,实现对机动目标,特别是非合作机动目标的高精度实时跟踪,成为地面测控系统急需解决的问题。

传统的非合作机动目标跟踪方案包括3个方面:

1)建立动力学模型,通常包括高斯白噪声加速度模型及马尔科夫随机过程加速度模型[1-3]。白噪声加速度模型假设加速度特性满足白噪声,并不符合实际,故收敛速度慢;马尔科夫随机过程加速度模型假定加速度特性满足一阶马尔科夫过程,比较符合实际,但对加速度的二阶特性没有准确描述。

2)建立非线性滤波器,常用的工程算法包括扩展卡尔曼滤波器(EKF)与无迹卡尔曼滤波器(UKF),国内外相关文献很多[4-5]。

3)制定机动检测策略[6-13],常见的机动检测策略包括基于测量新息及其统计特性检测与基于输出状态估计检测。

虽然已经发展了许多非合作目标跟踪算法,但对于幅值及时间均未知的脉冲推力控制下的非合作机动目标跟踪问题,研究的还不够深入,为此,文中在传统方案基础上,提出新的改进措施,旨在实现随机脉冲推力控制下非合作目标的连续平稳精确跟踪,在动力学模型方面,提出a-β动力学模型,在马尔科夫随机过程加速度模型基础上,引入辅助变量β,对推力加速度二阶特性进行准确描述,提高算法收敛性和精度;在机动检测策略上,考虑到运动学模型对机动的敏感性,提出运动学模型下的轨道信息机动检测策略。

1联合滤波器设计

文中从空间机动目标的跟踪与检测入手,设计一种联合滤波器接收观测数据,完成状态估计与机动检测,其处理流程如图1所示。

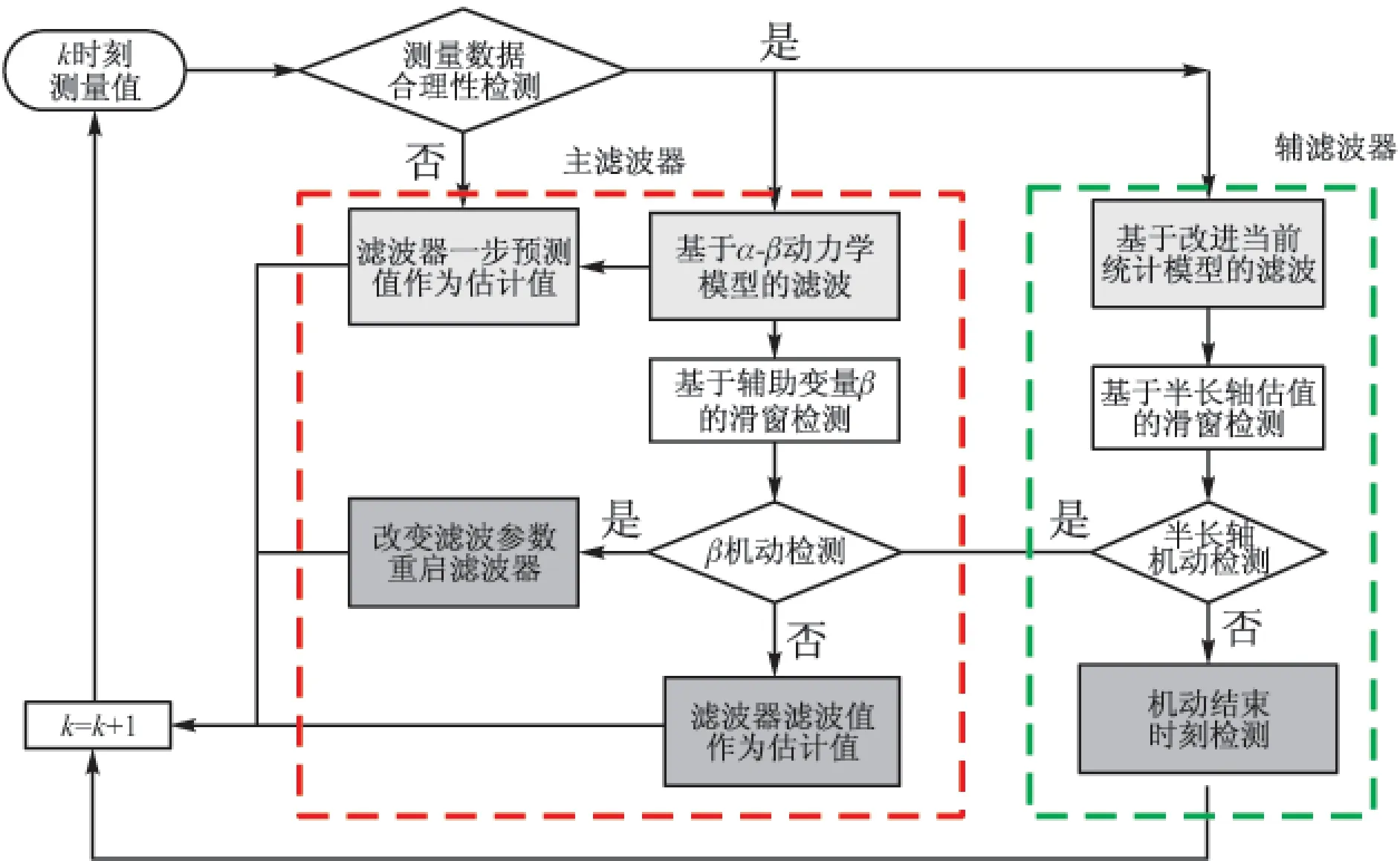
图1　联合滤波器跟踪非合作目标流程图

主滤波器,从动力学模型入手,通过引入辅助变量,对推力加速度建立恰当的微分模型,避免卫星质量和比冲的不确定性引起推力加速度的估计误差,可获得更快的收敛速度和滤波精度。同时,利用模型的辅助变量β物理特性,作为辅助机动检测判断,其输出值作为目标的跟踪结果。

副滤波器,从运动学模型对观测信息的敏感性入手,采用改进当前统计模型,具有很强的机动敏感性及自适应性,同时将滤波输出转化为轨道信息,从半长轴的变化监测目标是否发生机动,其输出结果作为目标检测的主要判据。

对于已经检测出来机动的滤波器,需要通过调整滤波参数P和Q完成多模型切换,提高状态方程与飞行状态的匹配程度,也可采用重启滤波器的方式获得更快的收敛速度和滤波稳健性。

2主滤波器设计

2.1基于a-β动力学模型的建立

(1)

式中:r为目标相对地心惯性系的位置矢量;v为目标相对地心惯性系的速度矢量;a为目标相对地心惯性系的推力加速度,在推力加速度未知情况下可设为0,在滤波估计中进行实时估计。β为推进发动机质量消耗量与当前质量比,在未知情况下可设为0,在滤波估计中进行实时估计。

其中:J2=1.082 63×10-3为二阶带谐项系数;μ=3.986 005×1014(m3/s2)为地球引力常数;地球赤道半径Re=6 378 140.0 m。

式(1)可以应用各种非线性滤波算法求解,常用的包括EKF和UKF。UKF以UT变换为基础,采用确定性采样获得预测信息,性能优于EKF。文中采用UKF[5]滤波算法获得更高的跟踪精度。

2.2基于状态信息的β机动检测

基于状态信息的β机动检测方法[7],通过分析加速度模型中辅助变量β的物理特性,为机动脉冲后沿检测提供依据,检测流程如下:

步骤1初始化。对于非合作目标,初始加速度未知,故设置初始状态a=β=0。

步骤2当目标机动时,辅助变量β会发生变化,当β<0时,与β的物理意义不符,此时可以判断脉冲机动结束。

步骤3考虑到脉冲机动时刻很短,基于状态信息的β机动检测可以准确及时的检测脉冲机动。

3辅滤波器实现

3.1基于当前统计模型的滤波

随机脉冲的机动是一种动力学特性未知的情形,可通过目标运动学信息建立随机过程逼近运动状态,而当前统计模型的要义是:利用修正瑞利分布函数描述目标当前加速度概率密度,更加符合目标机动范围和强度的实际变化,同时,其均值和方差之间存在关系,以此可以用来建立卡尔曼滤波的自适应算法。因此,这里的辅滤波器采用当前统计模型。

当目标以某一加速度机动时,采用零均值模型不合理,采用加速度的非零均值时间相关模型,即令:

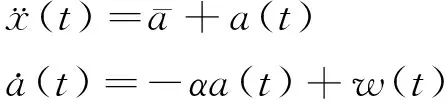
(2)

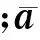
(3)

由于该算法可根据机动加速度自动调整方差,具有很好的自适应性,但是需要预先给定机动频率和加速度极值,而这些参数对于非合作目标是很难实现的,因此提出一种改进当前统计模型,利用位移公式及测量新息(预测值与观测值之差),实时在线估计加速度方差,提高算法的自主运行能力。

依据位移公式,可得位移预测值:

(4)

而位移实测值为:

(5)

则测量新息为:

(6)

考虑到测量过程中存在的零均值高斯白噪声,测量新息为:

(7)

目标加速度变化与观测随机误差是独立的,可得:

(8)

因此可建立测量新息与加速度变化量之间的关系,实时在线估计加速度方差。

(9)

当目标发生机动时,运动模型发生变化,预测新息与实际观测值出现偏差,机动越大,偏差越大,由式(9)可知,测量新息偏差与加速度方差成线性关系,导致机动加速度的方差增大。因此,文中的方差计算方法可以与目标的机动程度相适应,提高机动灵敏性。

3.2基于轨道根数估值的机动检测

由计算经验可知,运动学模型对测量信息的变化异常敏感,当目标发生机动后,轨道能量迅速发生改变,直观的变化是轨道信息的变化,例如半长轴、偏心率和倾角等[13]。检测相邻数据点间轨道半长轴的变化是否超过正常变化范围,就可以推测两点间是否发生机动。因此,可将半长轴的变化作为机动检测判据。

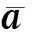
(10)

对于高斯分布,阈值α通常取值3～6。为了提出“机动野值”,降低检测虚警,可设置检测原则为连续若干点满足式(10)时为机动开始。

4仿真分析

下面仿真分析非合作空间目标机动过程中主副滤波器的性能。观测数据采用单站雷达仿真数据(R,A,E,dR),随机误差按照设备提供,测距50m,测速0.1m/s。仿真时长为2 150s,滤波初值误差考虑在3个方向的位置和速度上分别加20m和0.5m/s的常值误差。图2表示飞行器机动全过程三维弹道曲线;图3表示飞行器的机动控制加速度变化曲线存在5次随机脉冲机动;图4表示当不采用机动检测器时滤波全过程位置误差,在机动发生后位置误差逐渐增大、发散。

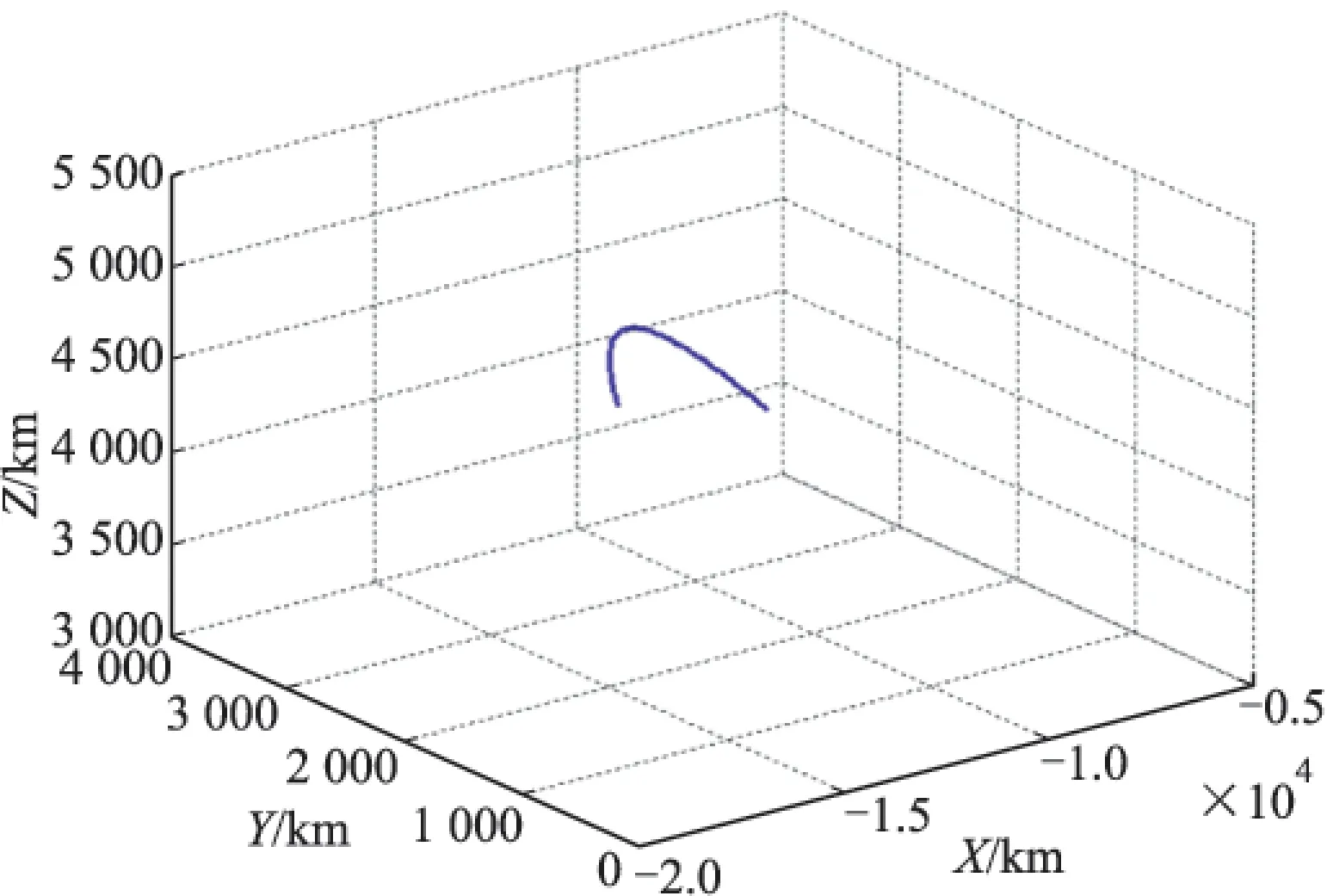
图2　空间目标三维曲线

图3　空间目标半长轴变化曲线

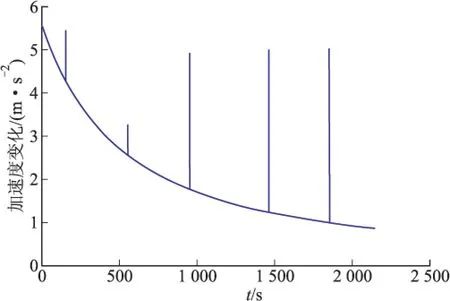
图4　空间目标机动加速度变化曲线

4.1主滤波器的状态估计

图5给出了主滤波器采用a-β模型时的半长轴估计结果,滤波算法采用UKF算法,滤波过程并未进行机动检测,可见主滤波器跟踪曲线整体较为平滑,但在机动前后出现较大变化。图6为主滤波器通过基于辅助变量β检测滤波的结果,当检测到目标机动后,滤波器通过调整滤波参数P和Q完成多模型切换,实现快速收敛。

图5　无机动检测时的主滤波器轨道半长轴估值

图6　基于辅助变量β的主滤波器轨道半长轴估值

4.2副滤波器的机动检测

图7给出了辅滤波器采用改进当前统计模型时的半长轴估计结果,滤波算法采用UKF,从运动学模型对观测信息的敏感性入手,利用位移公式及测量新息,实时在线估计加速度方差,提高算法机动敏感性及自适应性,同时将滤波输出转化为轨道信息,从半长轴的变化监测目标是否发生机动,其输出结果作为目标检测的主要判据。

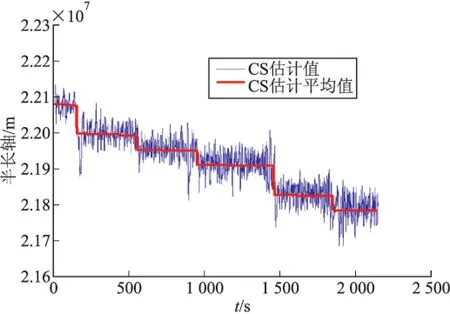
图7　副滤波器轨道半长轴估值

表1给出了传统当前统计模型与改进当前统计模型的机动检测时刻,由此可见两种方法检测基本时间相同,但传统当前统计模型需要设置加速度范围与机动频率,而改进当前统计模型不需要,具有自适应性。

表1　两种当前统计模型的机动检测时刻　　s

4.3主辅滤波器联合跟踪

图8为采用主辅滤波器联合跟踪非合作目标的轨道半长轴变化图,其中主滤波器引入基于辅助变量β的滑窗机动检测;辅滤波器引入基于半长轴估计值的滑窗机动检测,并将结果反馈给主滤波器。图8～图10为主辅滤波器联合跟踪非合作目标的位置、速度变化偏差图,从图中可以看出机动时刻位置偏差不超过100m,速度偏差不超过30m/s,非机动时刻位置偏差不超过40m,速度偏差不超过0.5m/s。

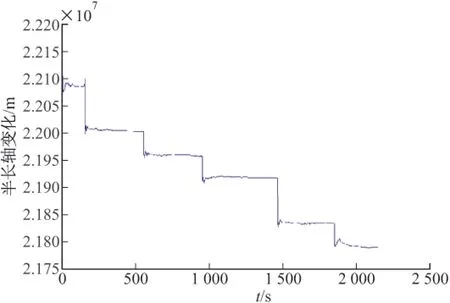
图8　主副滤波器联合跟踪的轨道半长轴估值

图9　主辅滤波器联合跟踪的位置速度总偏差

图10　主辅滤波器联合跟踪的三向位置速度偏差

5结论

文中针对随机推力控制下的空间机动目标跟踪精度问题,提出一种基于主副滤波器的实时跟踪算法。该算法建立主副两个滤波器,主滤波器采用动力学模型,通过状态约束完成空间非合作目标实时高精度跟踪;副滤波器采用改进当前统计模型,通过运动模型对观测信息的灵敏性完成机动检测。检测机动后,通过改变滤波参数获得更快的收敛速度和滤波稳健性。仿真实验验证了算法的有效性,同时获得如下结果:

1)仿真实验中测量数据质量高,在滤波重启后的初值可以准确获得,滤波算法可以快速收敛,收敛后跟踪曲线比较平稳;

2)主滤波器采用a-β模型,通过引入辅助变量β,对推力加速度建立恰当的微分模型,可获得更快的收敛速度和滤波精度;

3)从副滤波器的机动检测结果可以看出,目标机动共有5次,分别发生在相对时刻150 s,550 s,950 s,

1 461 s,1 851 s,与理论时刻基本一致;

4)改进当前统计模型与传统当前统计模型相比,对目标机动反应同样灵敏,但改进当前统计模型可以自适应进行机动辨识和跟踪,适合工程应用。

参考文献:

[1]LI X R, JILKOV V P. A Survey of maneuvering target tracking, part V: Multiple-model methods [J]. IEEE Trans. on AES, 2005, 41(4): 1255-1321.

[2]LI X R, JILKOV V P. A survey of maneuvering target tracking, part I: Dynamic models [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333-1364.

[3]LI X R, JILKOV V P. A survey of maneuvering target tracking, part II: Ballistic target models [C]∥Proceedings of 2001 SPIE Conference on Signal and Data Processing of Small Targets, CA, USA, 2001: 1-23.

[4]LI X R, JILKOV V P. A survey of maneuvering target tracking, confer ence part IV: Decision-based methods [C]∥ Proc. SPIE on Signal and Data Processing of Small Targets 2002: 1-5.

[5]JULIER S J, UHLMANN J K. New extension of the Kalman filter to nonlinear systems [C]∥ Proc. SPIE 3068 Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, 1997: 54-65.

[6]李恒年, 李济生, 黄永宣. 轨道机动过程中推力加速度的在线最小方差估计 [J]. 空间科学学报, 2002, 22(4): 357-362.

[7]黄普, 钱山, 李恒年. 应用观测新息和状态信息检测联合脉冲机动 [J]. 国防科技大学学报, 2014, 36(3): 164-168.

[8]NAMRATA V. Additive change detection in nonlinear systems with unknown change parameters [J]. IEEE Trans Signal Proc, 2007, 55(3): 859-872.

[9]范红旗, 王胜, 付强. 目标机动检测算法综述 [J]. 系统工程与电子技术, 2009, 31(5): 1065-1070.

[10]周宏仁, 敬忠良, 王培德. 机动目标跟踪 [M]. 北京: 国防工业出版社, 1991: 56-60.

[11]刘也, 余安喜, 张增辉, 等. 空间目标跟踪的稳健融合方法与实现 [J]. 系统工程与电子技术, 2011, 33(9): 1941-1947.

[12]张振军, 董云峰. 基于小波分析的目标轨道机动自主检测方法 [J]. 北京航空航天大学学报, 2008, 34(13): 353-356.

[13]于大腾, 王华, 尤岳, 等. 不完备轨道信息下的LEO轨道面内机动检测方法 [J]. 宇航学报, 2013, 34(3): 314-319.

*收稿日期:2015-04-27

基金项目:国家自然科学基金(61302098)资助

作者简介:黄普(1982-),男,陕西韩城人,工程师,硕士,研究方向:飞行器控制系统。

中图分类号:TP316

文献标志码:A

Non-cooperative Target Precision Tracking Technology Based on Input and Orbit Information

HUANG Pu,SUN Shouming,LI Hengnian

(State Key Laboratory of Astronautic Dynamics, Xi’an 710043, China)

Abstract:A new method was presented based on input and orbit information for space non-cooperative target tracking during random thrust maneuvering process. It is composed by two filters in parallel, the main one is constructed by dynamic model and the auxiliary one is constructed by improved current statistic model. The two filters run for estimating real-time and precise filtering results. Meanwhile, maneuver detection is done based on the orbit information. If the maneuver is detected, changing filter parameters are introduced to obtain faster and smooth tracking results. Simulations show that the result of the new algorithm is much superior to traditional ones. The algorithm has certain engineering practicability.

Keywords:input and orbit information; a-β dynamic model; improved current statistic model