国外数学课堂互动模式的梳理及启示

李　娜，李　卓



国外数学课堂互动模式的梳理及启示

李娜，李卓

摘要：数学课堂交流，尤其是教师与学生间的互动是课堂教学进行有效交流的关键渠道。通过对国外教育核心期刊中所发表的文章进行梳理发现，数学课堂中的互动模式主要有三种：漏斗模式、聚焦模式以及触发-回应-评价/反馈模式。通过具体课堂实例说明这三种模式的特点以及国内相关研究的基本情形，教师要充分重视课堂中对学生的提问与反馈，尤其是在反馈方面。

关键词：数学课堂交流；交流模式；教师反馈

一、研究背景

在数学课堂研究方面，课堂交流的重要性已被越来越多的研究者所关注[1]，其中尤以作为课堂交流重要来源的师生互动所受到的关注更多。[2]众所周知，教师在课堂交流中扮演着重要的角色。研究发现，教师如果能积极主动地帮助学生参与到课堂交流中，学生将会更容易进入有意义且持续的学习过程。由于其重要性，许多国家将其列在其官方文件中。美国教师协会NCTM指出，教师应该在课堂上鼓励学生对问题提出解决方法或猜想，通过交流，学生能巩固对数学的理解，丰富问题解决的策略。最新澳大利亚课程标准明确强调数学学习要保证学生变成有自信，有创新性的数学应用型人才和交流者；能够探究、呈现以及解释工作中和生活中出现的数学现象。由此看出，学生在实际生活中的数学应用也离不开数学的交流。[3]英国最新的课程标准进一步指出，交流中离不开语言的使用，语言在学生学习课程的过程中起着非常重要的作用，因为学生听到的语言质量和多样性会影响他们的数学表达能力，尤其在数学证明方面，教师必须帮助学生学会利用课堂中的交流讨论来刺激或纠正学生错误的数学概念。[4]新加坡课程政策中指出，学生在课堂上不但要有探讨、论证数学的机会，还要有交流数学的机会, 而且课标中明确指出，在数学课堂上培养学生在交流中具有使用数学语言来精确、简洁、合逻辑性地表达数学想法和争议的能力。[5]这样可以帮助学生发展自身的数学理解力并不断提升自身的数学思考能力。

除了国外官方政策文件中有表明课堂交流在数学教学中的重要作用外，在我国最新颁布的课程标准中也强调教师作为学生学习活动的组织者、引导者、合作者，要为学生创造足够的时间和空间，经历观察、实验、猜测、计算、推理、验证等活动过程。不难看出，教师在课堂交流中起着重要的作用，尤其在我国的数学课堂中，课堂交流基本上皆由教师引起。基于此，本文要着重研究的问题是：国外数学课堂互动的主要模式有哪些？这些互动模式适用于我国的数学课堂吗？教师采取怎样的策略能更有效促进数学课堂交流？

二、文献梳理过程

从上面可以看出，数学课堂交流的重要性已经体现在官方的课程政策中。考虑到国外学者对数学课堂交流这一问题的研究视角与我国学者的研究也有不同，国外学者关于数学课堂交流的研究怎样呢？本文主要的文献来源于英语文章以及书籍。首先阅读相关文献确定与课堂交流有关的关键词：classroom interaction, classroom communication, teacher questioning, teacher verbal feedback等，然后利用这些关键词进行更为详细地文献搜索。为保证文章质量，所选文章皆来自教育领域的顶级期刊，如，ReviewofEducationalResearch(Education&EducationalResearch1out224)，EducationalStudies，LearningandInstruction等期刊的文章以及专门介绍数学课堂交流的书籍Alternativepatternsofcommunicationinmathematicsclasses:Funnelingorfocusing?等。通过分析后发现，国外学者关于数学课堂互动的研究主要集中于数学课堂互动模式的研究。因此首先逐一介绍几种主要的数学课堂交流模式并尝试用我国数学课堂中的例子来解释说明这些模式，然后分析所存在的问题，以期能够对我国的数学课堂交流研究有所启示。

三、数学课堂交流模式

通过对文献的梳理归类发现，数学课堂互动的模式主要有三种：漏斗模式 (Funnel Patter)、聚焦模式 (Focusing Patter)以及触发-回应-评价/反馈模式 (Initiation-Response-Evaluation/Feedback)。

(一)漏斗模式

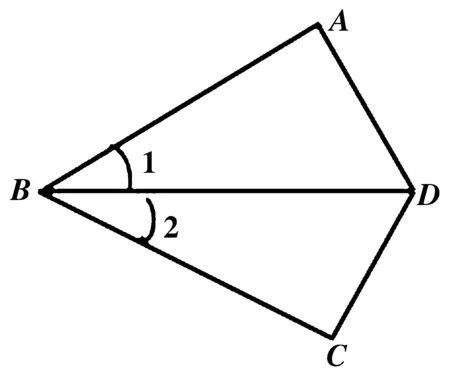
图 1

漏斗模式指的是当学生在回答教师提出的问题出现错误时，教师往往会努力去修正这些错误，在对错误的修正过程中，教师通常会鼓励学生自己修正。教师通过依次提问的方式，直到正确的答案由学生或者教师口中得出。[6](P213-232)这是一种比较常见的课堂交流模式。当学生给出不正确的答案时，教师不是简单地告诉学生答案不正确或是找其他学生给出正确答案。相反，教师先假装接受这个不正确的答案并且试着通过提出一些提示性问题，让学生重新思考自己给出的答案，直到帮助学生得到一个完全正确的答案[7](P167～168)，如下面的课堂示例所示：

示例1：已知：如图，AB=CB，∠1=∠2 ，△ABD和△CBD全等吗？

变式1：现在例1的已知条件不改变，而问题改变成：问AD=CD吗？BD平分∠ADC吗？

课堂实录

师：现在看变式1，例1中的条件不变，将问题改为AD=CD吗？BD平分∠ADC吗？你能证明吗？

很多同学：能。

师：好，能证明的同学站起来说一下怎么证。

生：已知条件告诉我们，在△ABD中，AB=CB，∠1=∠2，然后AD=CD，BD又等于?(学生犹豫)

师：你觉得我们要证明AD=CD，BD是∠ADC的平分线的话，需不需要证明全等？(问了一个与答案有关的问题)

生：需要。

师：需要，对不对？那怎样证明全等呢？(继续问与答案接近的问题)

生：BD=BD，AB=CB，还有∠1=∠2

师：边角边，好，两个三角形全等，那∠ADB与∠CDB？

生：相等。

师：由角平分线的定义可得？(已经接近答案)

生：BD平分∠ADC。

在此示例中，当学生没有立即给出正确的答案时，漏斗模式显现了。教师通过三个主要问题成功地将学生引向了正确答案。由三角形全等到其中的∠ADB与∠CDB，学生的思路被教师引导着。教师的这些问题就像是编制了一个漏斗，慢慢收紧过滤学生的答案，最终得到那个正确的答案。此种模式下，显而易见是学生跟随教师的思路在解决问题，而学生是如何思考这个问题的却不得而知。

所以，此种互动之下有两个很明显的缺点。第一个是不利于培养学生的数学学习兴趣。教师通过提问与学生密集讨论应对错误的策略或者迫使学生去不断进行尝试，这种情况下，学生很可能会强迫自己机械地记住曾经使用过的一些策略，或是造成学生由于害怕找不到正确答案而产生的心理或情感上的负担，最终很可能让学生失去学习数学的兴趣。另一个是限制学生在课堂学习中的能动性。漏斗模式中，教师制造出一系列与答案相关的教学策略来促使学生找到最终答案[8](P149-168)，但是因为密集型的提问并不能为学生提供充足的时间或者机会让学生亲自去尝试发现新的问题解决方式，从而限制了学生的贡献。[9]教师通过漏斗模式仅仅给学生准备了一个完成教师预设的问题解决方式而没有提供让学生尝试自己策略的机会。为了让学生有更多的机会来阐述他们的想法，研究者提出了下面将要讨论的第二种模式——聚焦模式。

(二)聚焦模式

在探讨漏斗模式中发现，学生需要更多的机会在教师或者同伴面前说出自己的想法。聚焦模式是对漏斗模式在学生回应方面的一种纠正。聚焦模式的实施是设计让学生有机会反思自己和他人想法的情境。也就是说，当学生在课堂上与他人交流的时候，教师应该创造一种允许学生对自己的想法给出解释或给出理由的氛围。不难看出，聚焦模式中，教师实际上将解决问题的责任返回给了学生。同时，这种模式还允许教师能以更清晰的方式理解学生的想法。[9]

示例2：柿子熟了，从树上落下来，下面的哪一幅图可以大致刻画出柿子下落过程中(即落地前)的速度的变化情况？

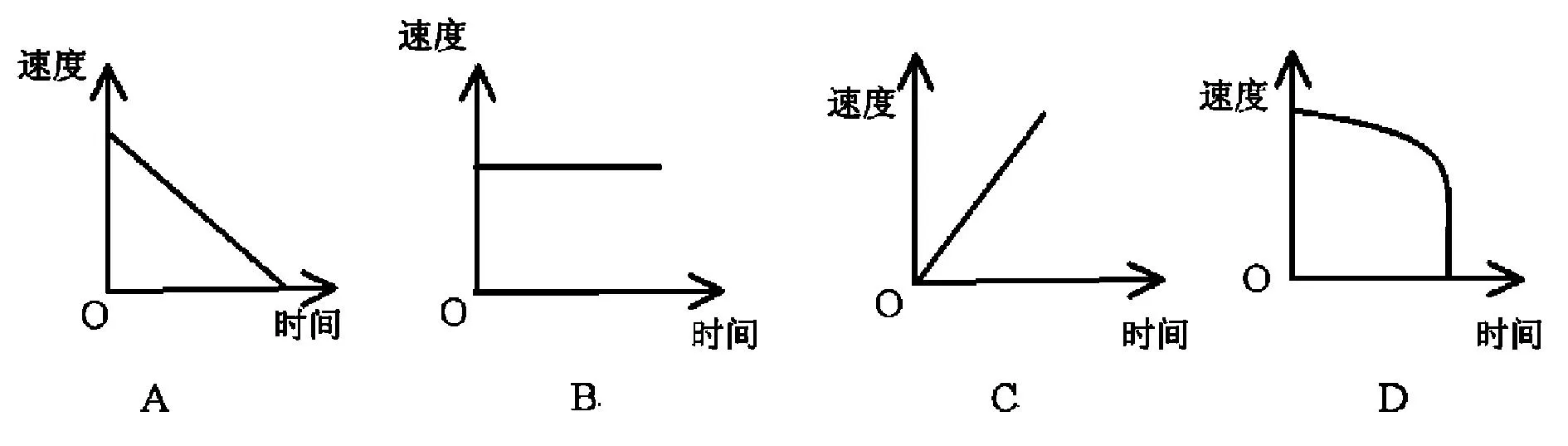
课堂实录

师：请同学来说出选择哪个答案并解释你为什么选择这个答案。蔡同学，你来说一下。

蔡同学：我认为应该选A吧？

师：那你给大家解释一下，为什么选A？

蔡：因为树高是个定值，柿子落地时与地面的距离越来越小，最后就没有高度了，所以选A。

师：同学们，听没听清蔡怎么解释这件事？

同学们：听清了。

师：他解释的对吗？如果不对，错在什么地方？

(没有同学回应，教师稍微一停顿。)

师：蔡同学说，柿子在树上，与地面有一定的高度，然后落下来了，没有高度了，所以他选A。

(教师指定了高同学来解释一下。)

高：我认为这道题与树的高度没有关系，看图像的横坐标与纵坐标，是速度和时间，这与树的高度没有一点关系，所以我认为选A不正确。

师：对，看图像的时候要注意图像的横坐标与纵坐标分别表示的是什么。(教师将横纵坐标的表示解释了一遍)，正确答案到底应该是什么？

同学们：C。

教师：谁能解释一下？(再一次让同学解释。)

最终经过3个同学的解释，终于解释明白，教师又将同学们的解释梳理了一下，然后继续讲课。

在这个例子中，虽然教师也是通过密集的提问，引导学生获得正确的答案，但是相比漏斗模式，最为明显的变化是学生展示思维过程的机会大大增加。学生在教师及同学面前展示自己的思维过程并解释自己的答案。此例子中，即使蔡同学的答案不正确，教师也依然要求学生给出自己的解释，而不是直接宣布正确答案或是按照漏斗模式用自己的思路给出提示，进而引导学生按照预设的思路获得正确答案。聚焦模式中，教师认为学生有责任将自己的答案解释清楚。在这种情况下，同学们更容易参与到课堂交流中来，因为答案是同伴给出而不是教师给出，学生挑战同伴答案的压力远远小于挑战教师答案带来的压力。我国课堂中最为常见的是漏斗模式的交流，但是从长远来看，还是聚焦模式更能让学生获益，无论是在学生的数学交流还是思考方面。

(三)触发-回应-评价/反馈模式

在触发-回应-评价/反馈模式(Response-Evaluation/Feedback)下，课堂教学可以被理解成由教师和学生创造的活动交替的过程，这种交替其实就是由三部分衔接而成：触发(Initiation)、回应(Response)、评价(Evaluation)。触发通常由教师的提问产生，紧跟着学生的回应，然后是教师对学生回应的评价。由于教师很可能只会让学生阐述他们的答案而不是去评价学生答案，所以第三个环节也通常被解释为反馈(feedback)或是跟踪(follow-up)。这个基本互动序列通常被叫做“IRE” (Initiation-Response-Evaluation)，或者 “IRF” (Initiation-Response-Feedback/Follow-up)。[10]这种情况在课堂中比较常见。

示例3：IRE (触发-回应-评价)或 IRF(触发-回应-反馈/跟踪)。

师(触发)：谁能起来用语言表述一下单项式乘多项式的法则呢？没事，大胆说，说错了也不要紧，(看到还是没有同学举手)，我要点名提问了。

生(回应)：呃，那就是，应该是?(学生在犹豫是否该继续说下去)

师(跟踪)：按照自己想的说就行。(教师坚持继续鼓励学生说出自己的想法)

生(回应)：那就是，这个，是这个单项式分别乘这个多项式中的每一个单项式。

师(评价)：说得怎么样？挺好的吧？对吧？

从上面的例子中不难看出，学生只需说出多项式乘多项式法则即可，不需要展示什么其他的想法，教师只需要给出个回应。这种模式(指IRE或IRF)是数学课堂最为流行的模式[11]，尤其是教师让学生回答一些简单的口头计算问题的时候。这种模式下的信息一般都是提前设定好了，由于这种模式太依赖于教师角色的定位以及教师怎样利用反馈，所以有研究者认为这种结构限制了课堂中的数学学习[12](P43-66)，但近来越来越多的研究者认为这种互动是课堂交流所必不可缺的，是一种重要的教学渠道。[13]想要高效地利用这种模式，教师应该重点关注能体现学生想法的片段而不是仅仅简单使用IRF模式，所以这也促使研究者利用课堂录像来帮助教师回顾反思自己的教学过程中对学生想法的处理，从而帮助教师改进教学方式，提升学生学习数学的兴趣。[14](P94-103)

(四)对三种模式的小结

从以上分析不难看出，每种课堂交流模式都有其特点。漏斗模式可以展示教师解决问题的思维方式让学生来学习，然而此种情形下，学生是被教师预先设计的问题解决思路所引导，不利于学生展示自己的想法。聚焦模式中，教师的聚焦点在学生的解决策略方面，让学生解释自己策略同时也让其他学生来评价，进而确保更多学生参与到课堂交流中来并从中获益。在IRE或是IRF中，教师有些时候很可能只给出一个评价性的反馈而不关注学生的想法，也不在意自己的想法能否展示给学生，所以教师的反馈显得尤为重要。可见，在数学课堂交流中，教师的提问要在学生回应之后还能进一步跟进，并与这节课的教学目标紧密相关。

漏斗模式在进行一些证明性的教学时或许更好用，让学生通过跟随教师的想法来厘清证明思路。如果特别需要了解学生想法时，就需要聚焦模式，让学生自己解释答案。而IRE或IRF的模式更适用于一些简单知识或是回忆性知识的教学。

四、教学策略

李祎通过近年的观课、研课发现，目前课堂上师生的表层交流比比皆是。[15](P198-199)比如，教师有时候为了提问而提问，为营造出一种热烈的课堂氛围而提出一些毫无启发性的“短平快”问题。另外，数学课堂中经常会出现教师对学生的想法表现出“虚假倾听”或是“不健全倾听”的现象，从表面上看，教师是在倾听学生的论述，但是内心并没有真正留意学生的想法。显然，这种形式上的交流对学生的智慧几乎产生不了什么大的影响。想要创造有意义的师生互动，教师的提问和反馈才是最主要的策略。[16]

(一)提高教师提问的质量

国内对于课堂提问的研究较为关注，在此不再赘述。很多时候，教师提问的问题过于简单，只需要学生回答“是”或“不是”；“对”或“不对”。教师很多时候也只是要求学生给出结果就可以，不追问学生的思维过程。只有有意义的提问才能引发学生积极的思考并可展现学生的思维方式，因此，应该多提出开放性的问题。教师应尽可能多地采用启发式进行提问，以给学生创设良好的情境，供学生积极思考并给出丰富多彩的答案，同时也让教师在与学生的思维碰撞过程中产生自己的教学灵感。

(二)重视教师反馈的作用

教师的反馈是教师教学中一种非常重要的教学行为，对学生的学习有重要的影响。[16]因为教师的反馈可以对学生的学习行为产生重要影响。学生利用教师的反馈信息来调整接下来的行为并完成自身认可的目标，同时，教师利用这种反馈对教学过程进行合理地调控。所以不难看出，教师的反馈在教学中的作用非常关键，它通常发生在教师与学生的互动过程中。[17]当然，教师的反馈不仅仅用来判断学生的回答正确与否，很多时候更要用一种积极的态度去鼓励学生的想法，让学生大胆参与到课堂交流中。

虽然本文介绍的主要是国外数学课堂交流模式，但是通过所提供的课堂实例发现，这三种教学模式也时刻发生在我国的数学课堂上。尤其是我国的数学课堂交流基本以教师引导为主，这三种模式也可以说是我国数学课堂交流中的基本模式。在师生互动中，教师的提问和反馈起着重要的作用。如果没有教师的反馈，师生互动不可能发生，学生的课堂学习也几乎不可能进行。若教师只是单纯地告诉学生答案的正确与否，那么反馈对学生的学习就没有任何影响。当他们尝试去指导学生并且在这个过程中提供正确答案的时候，影响就会变得强烈。这有赖于教师帮助学生学习时所采用的知识搭建模式，给学生创造的反思机会，以及让学生自我表达的程度。总之，积极的数学课堂交流会对学生的数学情绪产生积极的影响。

参考文献：

[1] Knuth, E., & Peressini, D. Unpacking the nature of discourse in mathematics classrooms[J]. Mathematics Teaching in the Middle School,2001(5).

[2] Jurik, V., Gr?schner, A., & Seidel, T. How student characteristics affect girls’ and boys’ verbal engagement in physics instruction [J]. Learning and Instruction,2013(23).

[3] Assessment and Reporting Authority, A. The Australian Curriculum Mathematics[EB/OL].(2011)[2016-06-09]. http://www.australiancurriculum.edu.au/Mathematics/Rationale

[4] Department of Education, G. U. National curriculum in England: mathematics programmes of study[EB/OL].(2014-07-16)[2016-06-09].https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes-of-study

[5] Ministry of Education, S. Secondary Mathematics Syllabuses[EB/OL].(2013)[2016-06-09]. https://www.moe.gov.sg/docs/default-source/document/education/syllabuses/sciences/files/mathematics-syllabus-sec-1-to-4-express-n(a)-course.pdf

[6] Bauersfeld, H. Remarks on the education of elementary teachers [M]. Constructivism and Education, 1998.

[7] Wood, T. Alternative patterns of communication in mathematics classes: Funneling or focusing? In H. Steinbring, M. G. B. Bussi & A. Sierpinska (Eds.), Language and Communication in the Mathematics Classroom [M]. Reston,Va: NCTM,1998.

[8] Wood, T. Patterns of interaction and the culture of mathematics classrooms. In S. Lerman (Ed.), Cultural Perspectives on the Mathematics Classroom[M]. Dordrecht: Kluwer Academic Publishers,1994.

[9] Herbal-Eisenmann, B. A., & Breyfogle, M. L. Questioning Our Patterns of Questioning[J]. Mathematics Teaching in the Middle School, 2005(9).

[10] Ingram, J. Whole class interaction in the mathematics classroom: a conversation analytic approach(Unpublished doctorial dissertation) [D]. University of Warwick, UK. Retrieved from http://wrap.warwick.ac.uk/49627/1/WRAP_THESIS_Ingram_2012.pdf. Accessed 09 June 2016.

[11] Heritage, M., & Heritage, J. Teacher questioning: The epicenter of instruction and assessment [J]. Applied Measurement in Education, 2013(3).

[12] Koole, T. Teacher evaluations: Assessing ‘knowing’, ‘understanding’, and ‘doing’. In G. Rasmussen, C.E. Brouwer, & D. Day (Eds.), Evaluating cognitive competences in interaction[M]. Amsterdam:Benjamins, 2012.

[13] Roth,W. M., & Gardener, R. “They gonna explain us what makes a cube a cube” Geometrical properties as contingent achievement of sequentially ordered child-centered mathematics lessons[J]. Mathematics Education Research Journal, 2012(24).

[14] Kiemer, K., Gr?schner, A., Pehmer, A. K., & Seidel, T. Effects of a classroom discourse intervention on teachers’ practice and students’ motivation to learn mathematics and science[J]. Learning and Instruction, 2015(35).

[15] 李祎.数学教学生成论[M].北京:高等教育出版社,2008.

[16] Walshaw, M., & Anthony, G. The teacher’s role in classroom discourse: A review of recent research into mathematics classrooms[J]. Review of Educational Research, 2008(3).

[17] Shute, V. J. Focus on formative feedback [J]. Review of Educational Research, 2008(1).

[责任编辑：陈浮]

收稿日期：2016-06-01

作者简介：李娜，香港大学(香港 999077)教育学院博士研究生；李卓，湖北师范学院教育科学学院讲师。

中图分类号：G633.6

文献标识码：A

文章编号：1009-7228(2016)03-0061-05

DOI:10.16826/j.cnki.1009-7228.2016.03.013

A Literature Review on the Main Patterns of Mathematics Classroom Communication in Foreign Countries and Its Implication

LI Na，LI Zhuo

Abstract:Mathematics classroom communication, especially the interaction between the teacher and students plays the key role in efficient teaching. Three main patterns of mathematics classroom communication are reviewed in theses in foreign educational core journals: Funnel Pattern, Focusing Pattern and IRE/IRF. Specific examples are also provided for each pattern to illustrate their unique features and basic conditions of domestic related research. Through this illustration, teachers’ verbal questioning and feedback should be paid much attention in classroom teaching.

Key Words:mathematics classroom communication; communication model; teachers’ feedback