一种基音周期检测中减小中值平滑误差的方法

马 英， 陈 超， 陈善继

（青海民族大学 物理与电子信息工程学院，青海 西宁 810007）

一种基音周期检测中减小中值平滑误差的方法

马 英， 陈 超， 陈善继

（青海民族大学 物理与电子信息工程学院，青海 西宁 810007）

在语音信号处理中，常用的基音检测算法对于纯净语音信号的检测效果较好；然而，实际的语音信号都会受到背景噪音的影响，使得常用的检测算法不能达到最优化，为提高检测基音周期的准确性，可以在基音检测后处理中采用多种平滑技术，但大多情况下后处理基音周期估值仍然产生很大的误差，为此文章针对语音信号基音周期估值的中值平滑处理中，可能产生基音提取的误差，进行误差分析，提出一种减小中值平滑误差的方法。

语音信号；基音周期；中值平滑；误差

语音信号分析中，语音信号特征参数的提取是非常重要的，只有获取准确的特征参数，才可以进行有效的语音识别，其中特征参数基音周期在参数提取中尤为重要，它的准确性决定着合成语音时是否能够高效地体现原始语音的频谱［2］。

而常用的基音周期检测算法都会产生检测误差，为了减小误差，可以采用各种平滑处理，常用的平滑处理技术主要有：中值滤波平滑技术，线性平滑技术，动态规划平滑技术。线性平滑处理虽然可以增加平滑的效果，但是可能导致两个平滑段之间阶跃的模糊程度加重，增加基音提取的难度；动态规划平滑处理采用的算法复杂度较高；而中值滤波平滑处理是最早兴起的，易于实现，可以较好地去除少量的“野点”，又不会使两个平滑段之间的阶跃性发生变化，但若原始信号中，某一点本身就是突变的，容易产生误差，从而得不到最准确的基音周期，文章针对语音信号基音周期检测的中值平滑处理产生的误差进行实验分析，提出减小误差的方法，提高基音周期检测的准确性。

1 原理基础

1.1 中值平滑技术

中值平滑是平滑技术中最常采用，原理简明，它的基本原理是：设x为中值滤波器的输入信号，y为输出信号，采用一个滑动窗，输出值就是将窗外的中心搬移到n处时窗口输入样点的中值，及n点处左右各取s个样点，与平滑点中心共同构成一组信号采样点（共2s+1个样值），然后将这（2s+1）个样点按大小顺序排成一排，平滑器的输出为该序列的中间值。s值一般为1或2，那么中值平滑起的“窗口”一般包含3到5个样点［1］。

1.2 线性平滑技术

线性平滑技术是采用滑动窗进行线性滤波处理，即

线性平滑处理不仅可以纠正输入信号中不平滑处的样点值，也可以修改附近各样点的值。

1.3 动态规划平滑技术

动态规划平滑处理的基本思想是：设计合理的代价函数，寻找使最终的合计代价最小的路径，它必须考虑与分析信号帧左右相邻的帧，并且在寻找最小代价的路径时，使用从前向后，从后向前，或从中间开始三种算法处理，算法复杂度高。在实际平滑处理中很少采用。

2 实验结果与分析

在实验检测中，采用Cooledit在普通室内环境下录制的男声语音信号，采样频率为44kHZ，单声道。

2.1 语音信号预处理

对输入的语音信号进行预处理，主要是为了对语音的高频部分进行加重，提升高频特性，增加语音的高频分辨率。［4，21］

MATLAB中的FDATool（FilterDesign&Analysis Tool），可以完成多种滤波器的设计分析。

在MATLAB命令窗口输入“fadtool”调出FDATool。输入滤波器参数得到相应的滤波器，

Fs=44000； %Sampling Frequency

Fpass=600； %Passband Frequency

Fstop=700； %Stopband Frequency

Dpass=0.057501127785；

Dstop=0.031622776602；

flag='scale'；

［M，W，B，T］=kaiserord（［Fpass Fstop］/（Fs/2），［1 0］，［Dstop Dpass］）；

b=fir1（M，W，T，kaiser（M+1，B），flag）；

Hd=dfilt.dffir（b）；

如图1所示：

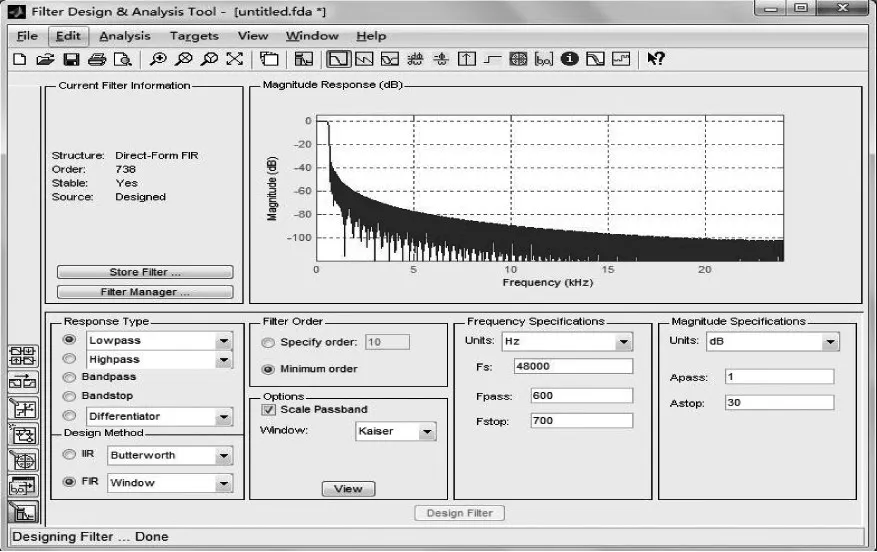
图1 FDATOOL设计滤波器

输入语音信号进行预处理，由图2中可以看出，预处理后的语音信号在高频部分的幅度得到了提升，使信号的频谱变得平坦，更能有效地提取语音信号的特征参数。

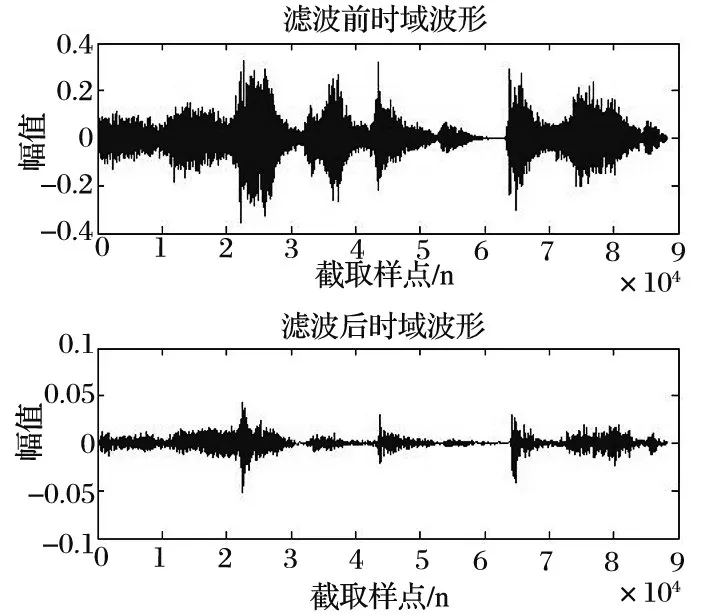
图2 预处理前后的语音信号

2.2 基音周期估值的中值平滑处理

在实验检测中，一般窗长应选为基音周期的两倍以上，才会有较好的效果，语音中最长基音周期大约为20ms，故在基音周期估值时窗长选为40ms效果比较好［1］。设置分帧长度，取40ms，即1764个样点，取50帧语音信号进行实验分析，提取各帧基音周期，如图3所示。

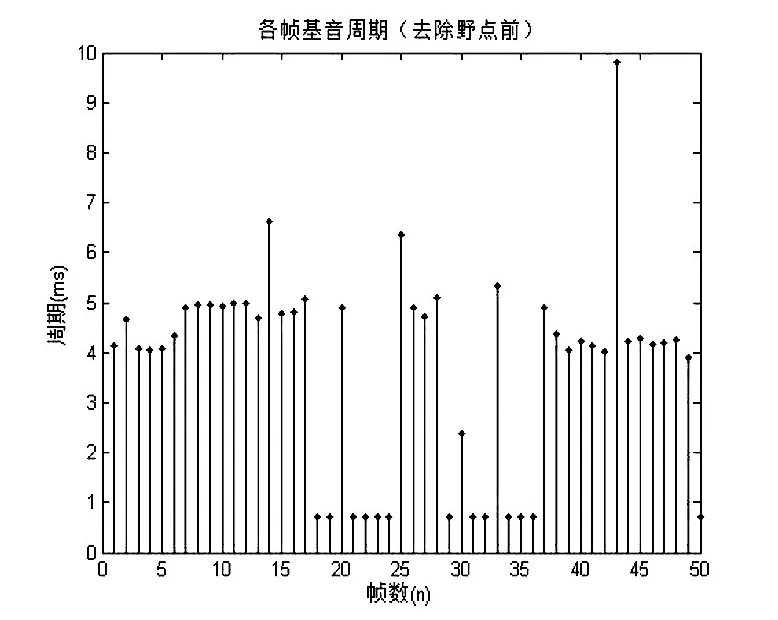
图3（a）ACF提取基音周期

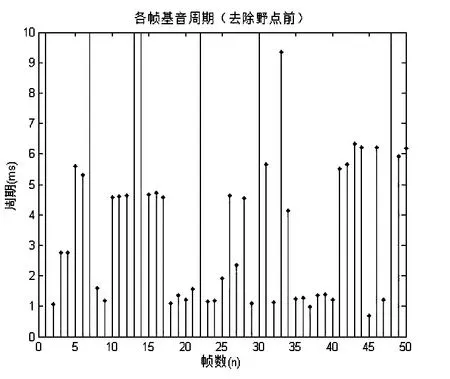
图3（b）CEP提取基音周期

由图3（a）和图3（b）可见在去除野点前两种基音检测方法都出现了较大的误差，使得基音周期轨迹中有几个基音周期偏离了原有的轨迹，这种偏离点即为基音轨迹的“野点”。而这些“野点”在基音周期检测中会造成基音周期的误判，因此对该50帧语音信号继续进行中值滤波平滑处理，如图4所示。

图4（a）ACF中值平滑分析

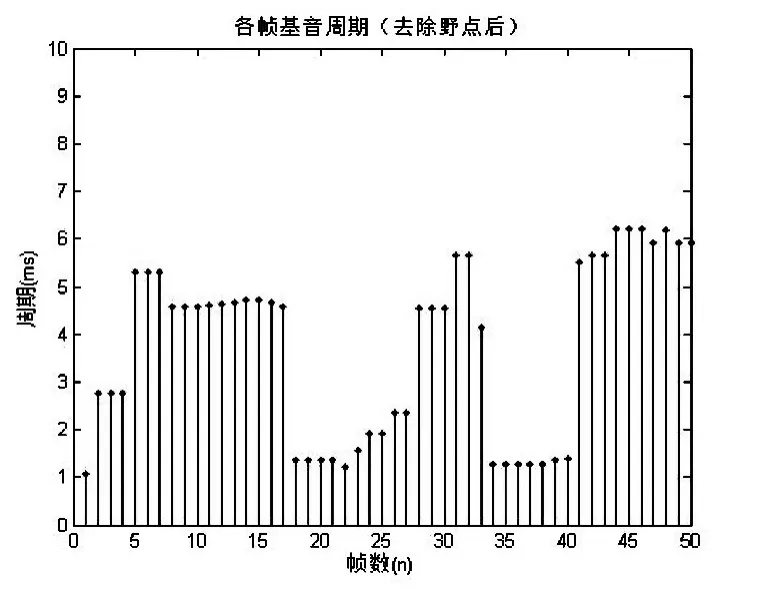
图4（b）CEP中值平滑分析

在图4（a）和图4（b）中进行中值平滑处理去除野点后，两种基音检测结果差距减小，50帧信号的基音周期大部分在4ms-6ms之间，但仍然有个别帧信号偏离了基音周期的正常轨迹，产生了一定的误差。

2.3 减小误差的方法

实验中提取中值滤波后偏离基音轨迹的第20帧语音信号做进一步分析。

第20帧语音信号进行提取基音周期，如图5所示。

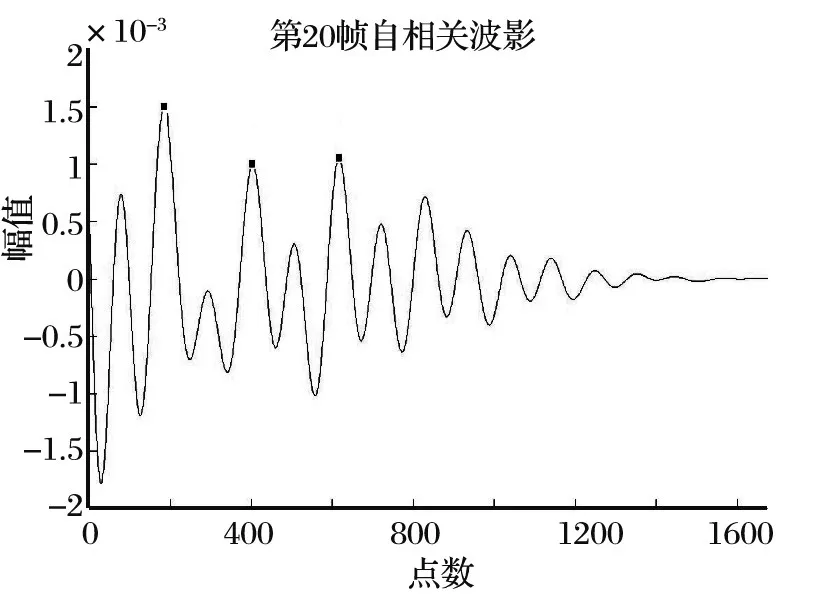
图5 第20帧语音信号ACF

在语音信号中，对于浊音的ACF，具有一定的周期性，进行一定的采样后，ACF具有最大值，可用ACF的相邻峰值点的距离来估算浊音的基音周期。由于一般语音信号基音频率不会低于40Hz，最大不会高于1000Hz，在实验检测中，去掉前面有可能的错误值，防止误判，但是，在计算基音周期时，必须补回去掉的样点数，算出对应的基音周期约为T=（相邻峰值点的距离+去掉的样点数）/采样频率。

由图5（图中已去掉前40点）得：

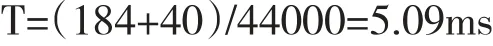
检测结果基本在基音周期的轨迹曲线上，与前面50帧信号检测出来的基音相比周期误差较小。

第20帧语音信号进行CEP提取基音周期，如图6所示：

图6 第20帧语音信号CEP

由图6难以读出这帧信号的最大值，倒谱近乎直线。在利用MATLAB的“max”函数判断时最大值的横坐标是127，在倒谱法中，浊音语音的基音周期可用倒频谱的最大峰值点的倒数来估值，其基音周期为

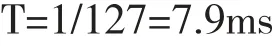
检测结果偏离基音周期轨迹曲线，与前面50帧信号检测出来基音周期有较大的误差。重复上述实验，发现中值平滑处理后基音周期检测时，无论采用什么方法个别帧仍然会产生较大的误差，在这种情况下，对语音信号中值滤波平滑处理后采用多种方法提取基音周期并求得平均值，即

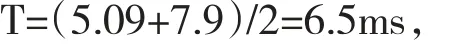
可以得到相对准确的基音周期。

3 结论

针对声学特征提取基音周期时，可能产生基音周期检测的错误，文章采用了短时自相关和倒谱检测算法后进行中值平滑后处理，虽然提高了基音周期检测的相对准确性。但是，个别帧基音周期检测准确度并不是很高，中值平滑输出后基音周期检测仍然存在误差，因此，通过实验分析，提出了中值平滑处理后用两种以上的方法共同求同一帧语音信号的基音周期，然后求平均的方法，可以得到相对准确的结果，此方法可以减小语音信号中值平滑处理中产生的相对误差。

［1］赵力.语音信号处理版［M］.北京：机械工业出版社，2009：5.

［2］高西全、丁玉美.数字信号处理［M］.西安：西安电子科技大学出版社，2008：8.

［3］张志涌.精通MATLABR2011a［M］.北京航空航天大学出版社，2011：11.

［4］张雪英.数字语音处理及MATLAB仿真［M］.电子工业出版社，2010：7.

［5］罗博、孙超.一种基于自相关函数的幂律检测器［J］.应用声学，2010，25（5）：352-355.

［6］顿珠次仁.藏语语音信号降噪算法研究［J］.西藏大学学报，2010，11（25）：251-255.

［7］敏生智、耿显宗.安多藏语会话读本［M］.西宁：青海民族出版社，2003.

［8］李洪波、于洪志.藏语语音识别的预处理研究［G］.中国中文信息学会二十五周年学术会议论文集，2006.

［9］Y.Fuji，K.Yamamoto，and S.Nakagawa.Hidden conditional neural fields for continuous phome speech recognition，IEICE Trans［J］.Inf.&Syst.，2012，95（8）：2094-2104.

［10］T.N.Sainath，D.Nahamoo，B.Ramabhadran，etal.Exemplar-based sparse representation phone identification features［J］.Proc.ICASSP，2011：4492-4495.

［11］G.Dahl，D.Yu，L.Deng，et al.Large vocabulary continuous speech recognition with context-dependent DBN-HMMS［J］.Proc.ICASSP，2011：4688-4691.

［12］王文延、曾庆宁.一种噪声环境下的语音端点检测方法［J］.声学技术，2007，26（3）：435-437.

［13］简志华，王向文.采用压缩感知的改进的语音转换算法［J］.声学学报，2014，24（3）：400-406.

［14］颜永红，李军峰，等.语音中元音和辅音的听觉感知研究［J］.应用声学，2013，22（3）：231-233.

［15］马永，贾俊芳.遗传算法研究综述［J］.雁北师范学院学报，2007，23（3）：11-13，21.

［16］韩阔业，江海，等.一种基于minimax准则的压缩采样信号检测方法［J］.中国科学院研究生院学报，2010，27（6）：794-799.［17］蔡铁，唐飞，等.采用子带长时信号变化特征的稳健语音活动检测［J］.电视技术，2014，38（19）：221-223.

［18］赵萍.语音信号的自相关基音周期检测［J］.上海电力学院学报，2011，27（3）：297-300.

［19］胡剑凌，徐盛，等.一种改进的基音检测算法［J］.上海交通大学学报，2000，34（6）：827-829.

［20］赵振东，胡喜梅，等.基于谱减法的基音检测算法［J］.计算机工程与应用，2008，44（5）：197-198.

［21］闵孝忠，朱林立.听诊采样仿真系统的设计与实现［J］.云南师范大学学报（自然科学版），2015，35（2），62-66.

In a Pitch Detection Method for Decreasing the Median Smoothing Error

MA Ying，CHEN Chao，CHEN Shan-ji
（School ofPhysicsand Electronic Information Engineering，QinghaiUniversity for Nationalities, Xining，Qinghai，810007，China）

In speech signal processing，commonly used pitch detection algorithm for clean speech signal detection effect is better；However，the actual speech signalwill be influenced by background noise，make the commonly used detection algorithm can notachieve optimization，In order to improve the accuracy of pitch detection，in pitch detection post-processing used in a variety of smoothing techniques，but in most cases the post-processing pitch valuationsstillproduce very big error，for thispitch for speech signal in the valuation of themedian smoothing，may produce the error of pitch extraction，detection analysis，put forward amethod to reduce themedian smoothing error.

Speech signal；Pitch period；Themedian smoothing；Error

O424

A

1008-9659（2016）02-0075-05

2015-03-15

青海民族大学科技合作基金（312000514315008）；青海省国际科技合作项目（2014-HZ-821）；青海省科技厅应用基础研究项目（2015-ZJ-721）。

马 英（1978-），女，青海西宁市人，副教授，主要从事信号处理研究。