基于空间模拟退火算法的最优土壤采样尺度选择研究①
2021-03-23王晓瑞周生路徐翠兰隋雪艳黄晓阳
王晓瑞,周生路,徐翠兰,隋雪艳,黄晓阳
基于空间模拟退火算法的最优土壤采样尺度选择研究①
王晓瑞1,周生路2*,徐翠兰1,隋雪艳1,黄晓阳3
(1 江苏省土地开发整理中心,南京 210017;2南京大学地理与海洋科学学院,南京 210023;3保利江苏房地产发展有限公司,南京 210018)
以研究区0.5 km × 0.5 km(尺度 a)网格的7 050个样点为基础,分别得到1 km × 1 km网格的1 757个样点(尺度 b),2 km × 2 km网格的444个样点(尺度 c),4 km × 4 km网格的110个样点(尺度 d),以土壤有机质(SOM)为目标属性,运用模拟退火算法对4种采样尺度的土壤样点进行优化选择,确定区域土壤调查的最优采样尺度。研究发现,通过模拟退火算法优化选择后,尺度a、b、c、d的最优样点数量分别为956、751、283和95个,优选的样点在空间上均匀分布。随着采样尺度的减小,采样点数量呈倍数增长,但对土壤属性的预测精度并没有相应比例的增加,且随着样点数量的增加,土壤属性预测精度的增加量逐渐减小。从样点数量与土壤属性预测精度综合来看,2 km × 2 km的采样尺度是最优的土壤采样尺度。
采样尺度;模拟退火算法;土壤有机质;土壤属性预测
对土壤要素空间分布的准确认识,是合理、持久利用土壤资源的重要基础,也是土壤学与地理学研究的热点之一。从19世纪末俄罗斯自然地理学家Dokuchaeiv 开展黑钙土调查以来,土壤调查已经历了百余年的发展[1-2]。由于不可能测得区域内所有位置的土壤属性,采样调查便成为获取土壤信息及其空间分布的基本方法[3-5]。
目前,常用的抽样调查方法有经典抽样方法和空间抽样方法。经典采样,如随机采样、系统采样等,简单易行、应用广泛,但通常需要大量样点才能全面准确地获取土壤性状的空间分布特征。空间采样方法是在地统计学的支持下,考虑区域土壤的空间自相关特性来设计采样点。这类方法要依赖于大量样本才能建立空间变差函数,适用于对土壤属性空间分布格局有一定先验知识的地区[6-7]。因此,在没有先验知识的陌生地区,经典抽样仍是土壤调查的首选方法,而在经典抽样的诸多样点布设方法中,按不同尺度的网格进行规则化样点布设是最为常用的样本空间构造方法[8-10]。
通常情况下,在陌生区域进行土壤调查时,由于没有先验知识,采样尺度无法确定,样点布设具有一定的盲目性,此时往往倾向于进行小尺度的密集采样,以求获得更为真实详尽的土壤属性信息,但密集采样费时、费力,且耗资巨大;而以大尺度抽样,又可能会由于抽样数量过少而造成信息缺漏,不能真实反映区域土壤属性的空间分布特征(图1)[11-14]。因此,如何选择最合适的土壤采样尺度,以最少的样点数量、最优的空间布局进行土壤采样,是区域土壤调查的关键问题。最优采样尺度的选择即是从不同采样尺度的大量样点中选择最优的样点空间布局,使得样点数量最少且土壤属性的推理精度最高,这是一个复杂的优化组合问题。
模拟退火算法(simulated annealing,SA)是一种通用概率算法,用来在一个大的搜寻空间内找寻命题的最优解。该方法在土壤样本设计过程中已有广泛应用,Brus 等[15]和van Groenigen 等[16]通过该方法来最小化土壤属性分布图的平均估计方差或最大估计方差,确定土壤样点的最优位置,对土壤布样方案进行了深入的研究。本文运用模拟退火算法,对不同采样尺度下的土壤样点进行优化选择:①确定不同采样尺度下样点的最优空间布局,使样点的推理精度最高;②确定不同采样尺度下的有效样点集,探讨用多少抽样点可以表征原始集合的精度;③确定区域土壤调查的最优采样尺度,为区域土壤调查及相关研究提供理论支持。
1 材料和方法
1.1 研究区概况
东海县位于江苏省东北部,地处34°11′ ~ 34°44′N、118°23′ ~ 119°10′E。东海县属黄淮海平原东南边缘的平原岗岭地,地势西高东低,东部平原区地势平坦,分布诸多的湖泊水库;西部地区地势起伏连绵,为岗丘区;中部地区为平原向岗丘过渡的缓坡区。东海县耕地资源丰富,土壤肥沃,气候适宜,水资源丰富,农业生产历史悠久,适合水稻、小麦、玉米等作物的种植,是国家116个基本农田示范区之一。
东海县地形复杂,土壤资源丰富,土类剖面结构、形态、基本属性及性质各异,全县土壤有棕壤、砂姜黑土、潮土、紫色土及水稻土5个土类,11个亚类,17个土属,46个土种。5大土类中,棕壤类分布最广,占全县面积的46.38%,主要分布于中西部地区,其次是砂姜黑土占39.52%,主要分布于东部平原区。
1.2 样品采集
从研究区东海县相关部门收集到了2003—2009年期间采集的土壤样品测试数据,共7 050个样点,样点在研究区范围内均匀分布,覆盖了整个研究区除水域及建设用地以外的其他所有地类,平均分布间距约0.5 km。以此数据为基础,根据不同网格大小得到4种不同尺度的采样点布设,分别构成4种采样尺度下的最大样点集(图2)。尺度a:0.5 km × 0.5 km尺度的采样点,每隔0.5 km一个样点,共7 050个样点;尺度b:在尺度a的样点集中每隔1 km选取一个点,得到1 km × 1 km尺度的采样点,共1 757个样点;尺度c:在尺度a的样点集中每隔2 km选取一个点,得到2 km × 2 km尺度的采样点,共444个样点;尺度d:在尺度a的样点集中每隔4 km选取一个点,得到4 km × 4 km尺度的采样点,共110个样点。
同时,于2009年11月,在研究区以非网格采样方式,均匀随机布设70个样点采集并测试土壤样品,构成本研究的验证数据集。
1.3 研究方法
以土壤有机质(SOM)为目标进行土壤采样尺度的研究,运用模拟退火算法对4种采样尺度的原始土壤样点进行优化选择,确定不同采样尺度下最优的样点空间布局及有效样点数量,由此确定区域土壤调查的最优采样尺度。模拟退火算法采用Sacks和Schiller[17]及康立山[18]推荐算法,根据算法流程,运用本研究数据,在matlab平台上对模拟退火算法进行编程实现。
模拟退火算法主要包括以下4个步骤:
1)分别从4种采样尺度的原始样点集中随机选择一组样点作为最优解,用最优解对有机质进行普通Kriging插值预测,计算初始解的均方根误差RMSE0。均方根误差计算公式如下:

式中:为采样点个数,S和C分别为验证点有机质的实测值和预测值。
2)对最优解作随机变动产生一组新解,本研究中,即是在初始解外的余集中随机选择一个点替换初始解中的点产生新解,对新解继续进行普通Kriging插值预测,并计算相应均方误差RMSE1,并计算Δ=RMSE1-RMSE0。
3)若Δ≤0,则接受新解为当前最优解;若Δ>0,则按Metropolis准则以概率接受新解,否则保留原解。
Metropolis准则:设从当前状态生成新状态,若新状态的能量小于状态的能量(即RMSE1< RMSE0),则将新状态作为新的当前状态;否则,以概率接受新状态[19]。概率的计算公式为:

式中:为(0,1)上均匀分布的随机数。
4)重复进行步骤2、3,判定是否满足终止条件,如果不满足回到步骤2继续,否则终止,输出最优解。算法的终止条件选择温度达到最低,即样点数为10。
2 结果与讨论
2.1 不同尺度土壤有机质的统计特征
4种采样尺度最大样点集土壤有机质的统计特征如表1所示。从尺度a到尺度d,区域土壤有机质的最小值逐渐变大,而最大值逐渐变小,有机质的极差明显减小,由47.1 g/kg减小至41.2 g/kg;到尺度d时,最小值显著大于其他3种尺度,最大值显著小于其他3种尺度,极差也明显小于其他3种尺度。随着采样尺度的增大,土壤有机质平均值、变异系数、峰度系数、偏度系数都有与之相似的规律:尺度a、b、c的各项统计数据相差较小,而尺度d的相应值要显著大于(小于)其他3种尺度。由统计结果看出,随着采样尺度变大,样点数量逐渐减少,土壤属性信息也随之有不同程度的损失,尺度越大信息损失越明显,数据统计特征也越来越偏离实际的分布情况,尺度d对区域土壤有机质的表征已明显偏离实际,不能准确反映研究区的土壤有机质分布特征。

表1 不同采样尺度土壤有机质统计分析
2.2 不同尺度土壤样点优化结果
对4种采样尺度的最大样点集运用模拟退火算法进行优化选择,结果如图3。尺度a的最大样点集7 050个,经过模拟退火后优选出956个样点,表明在0.5 km × 0.5 km的采样尺度下,用956个样点即可表达最大样点集的有机质统计特征,这956个样点构成了采样尺度a的最小样点集。尺度b、c、d的最小样点集分别为751、283和95个。这一结果表明,在不同尺度的最大样点集中,都存在一定数量的无效样点,这些样点的存在并不能对土壤属性的分布特征有新的贡献,舍弃这些样点后依然可以获得较好的土壤属性特征。
2.3 不同尺度采样点的优化过程
运用模拟退火算法对不同尺度土壤样点的优化过程如图4。由结果看出,不同尺度土壤样点的优化过程中,随着样点数量的减少,RMSE先减小,然后进入平稳变化阶段,最后样点数量极少时,RMSE又逐渐变大。
在样点数减少的过程中,RMSE先有一个减小过程,这一过程主要是由于样点数量较多时,离群数据点的存在而形成。从理论上讲,样点数量越多越能反映真实情况,但现实中无论以何种方式进行采样,或多或少都有一定数量的离群数据存在[20-21]。按概率来看,样点数量越多离群数据也越多,因此在退火优化过程中,样点数量减少时,RMSE先有减小过程,这一过程即是剔除离群数据的过程。在后期RMSE随着样点数量减少迅速变大,表明此时由于样点数量过少,剩余样点已不能反映原始样点的属性分布特征。
尺度a的7 050个样点优化减少过程中,RMSE由0.269 4开始逐渐减小,当样点数量为956个时,RMSE达到最小为0.262 1,表明最少可用956个样点即可代替原始7 050个样点的土壤有机质分布。当样点数量减少至800个,随着样点数减少开始迅速变大,当样点数为10个时,RMSE达到0.328 7,表明此时的样点已经不能反映原始数据的真实特征。尺度b的1 757个样点优化减少过程中,RMSE由0.278 7开始逐渐减小,样点数量为751个时RMSE最小为0.263 1,样点数量减少至10个时,RMSE达到0.361 1。尺度c的RMSE由0.287 2开始减小,样点数量为283个时达到最小为0.278 6,样点数量减少至10个时,RMSE达到0.376 7。尺度d的RMSE由0.373 4开始减小,样点数量为95个时RMSE达到最小为0.353 6,样点数量减少至10个时,RMSE达到0.524 6。
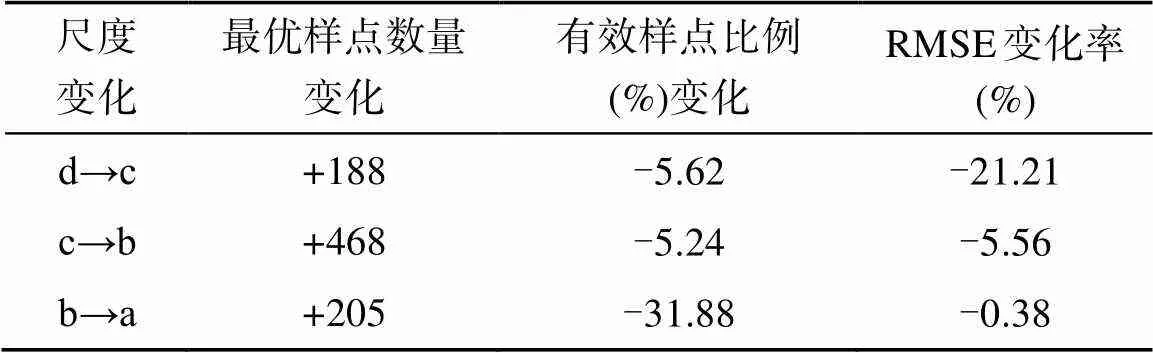
4种尺度土壤样点减少过程的RMSE比较发现,随着采样尺度的减小,RMSE总体在变大,尺度b样点减少过程的RMSE整体大于尺度a,而尺度c大于尺度b,尺度d又大于尺度c,即RMSEa 由以上分析发现,在不同尺度采样点的优化减少过程中,样点数量过多时,由于离群数据的存在而扰乱总体的数据分布特征,导致部分样点对土壤属性特征的表达没有有效的贡献。当样点数量过少时,由于关键位置样点的缺失而导致土壤属性表达不完整,不能准确反映土壤属性的分布特征。只有当样点数量在一定区间时,采样点才能较好地反映土壤属性的分布特征,这个区间即构成了该尺度下采样点布设的有效样点区间。在各尺度采样点的减少过程中RMSE均存在一个平稳变化的阶段,这一阶段中不同数量的采样点RMSE相差极小,均在最优解周围浮动,表明样点数量在这一区间时对土壤属性的预测结果均较好,都可以较好地反映原始数据的真实状况,这个RMSE平稳变化的阶段即是各采样尺度下的有效样点区间,在有效样点区间内RMSE达到最小的一组样点布设即为该尺度下最优的样点布局。 不同采样尺度下有效样点如图5。尺度a的有效样点区间为[800,4 100],占最大样点集的比例为11.35% ~ 58.16%;尺度b区间为[350,1 500],比例为19.92% ~ 85.37%;尺度c区间为[110,400],比例为38.29% ~ 90.29%;尺度d区间为[45,105],比例为40.91% ~ 95.45%。采样尺度越小,样点数量越多,有效样点区间也越大,但有效样点占原始最大样点集的比例越小;随着采样尺度变大,有效样点占原始最大样点集的比例越来越大。这表明采样尺度越小,样点的有效性越弱,样点布设中存在大量的无意义样点,会造成人力、物力的浪费。因此,从样点的有效性及工作效率来看,采样尺度的选择应该是越大越好,在本研究中尺度d(4 km × 4 km)的采样尺度下有效样点比例最高,样点数量少采样成本及效率也是最高的,而尺度a的样点有效性最弱且样点数量过大导致采样成本过高。 最优的采样尺度应该是保证土壤属性表达精度较高的情况下,样点有效性较强、样点数量较少的采样点布设尺度。因此,采样尺度的选择应从样点数量、样点有效性及土壤属性表达精度3方面综合考虑[22-23]。从尺度d到尺度a的样点数量变化、有效样点比例变化及RMSE变化如见表2。 表2 样点数量和误差随采样尺度变化的关系 注:“+”表示增加,“–”表示减小。 从尺度d到尺度c,采样尺度变小,原始样点数量增加4倍,最优样点数量增加188个,有效样点比例只减少5.62%,但RMSE减小了21.21%,对土壤属性的表达精度大幅增加,这表明采样尺度从4 km × 4 km(尺度d)减小到2 km × 2 km(尺度c)是很有意义的,较少的样点数量增加与有效样点损失,带来了精度的大幅增加。从尺度c到尺度b,最优样点数量大量增加468个,有效样点比例减少5.24%,RMSE只减小5.56%,对土壤属性表达精度的提升不甚明显,表明采样尺度从2 km × 2 km(尺度c)继续减小到1 km × 1 km(尺度b)无显著作用,样点数量大量增加但精度增加不明显。从尺度b到尺度a,最优样点数量增加205个,但有效样点比例大幅减少31.88%,而RMSE只减小了0.38%,对土壤属性表达的精度几乎没有提升,表明采样尺度从1 km × 1 km(尺度b)减小到0.5 km × 0.5 km(尺度a)亦无显著作用,样点数量大量增加、有效样点大量减少,而精度几乎无提升。 通过以上分析发现,尺度d对土壤属性表达精度不够,不宜在该尺度下进行采样点布设;而尺度b、尺度a样点数量过多,有效样点比例较低,对土壤属性的表达精度并没有比尺度c有明显的提升,尺度b、尺度a也不宜作为合适的采样尺度。因此,综合考虑,尺度c(2 km × 2 km)是本研究区最优的采样尺度。 1)采样尺度越小,采样点数量越多,对土壤属性的表达精度越高。从对土壤属性的表达精度来看,采样尺度的选择越小越好。 2)采样尺度越小,采样点数量越多,样点的有效性越弱,样点布设中存在大量的无意义样点,会造成人力、物力的浪费。从样点的有效性及工作效率来看,采样尺度的选择越大越好。 3)随着采样尺度的减小,采样点数量呈倍数增长,但对土壤属性的表达精度并没有相应比例的增加,且随着样点数量的增加,土壤属性表达精度的增加量逐渐减小。 4)采样精度与土壤属性表达精度总是一个矛盾的存在,对于土壤有机质来说,2 km × 2 km的采样尺度是本研究区最优的采样尺度。 [1] Soil Survey Staff. Soil taxonomy: A basic system of soil classification for making and interpreting soil surveys[M]. Washington, DC: United States Department of Agriculture, Natural Resources Conservation Service, 1999. [2] Webster R. Quantitative and numerical methods in soil classification and survey[M]. Oxford: Clarendon Press, 1979. [3] Gregoire T G, Valentine H T. Sampling strategies for natural resources and the environment[M]. New York: CRC Press, 2007. [4] 孙孝林, 王会利, 宁源. 样点代表性等级采样法在丘陵山区土壤表层有机质制图中的应用[J]. 土壤, 2014, 46(3): 439–445. [5] Brus D J, Noij I G A M. Designing sampling schemes for effect monitoring of nutrient leaching from agricultural soils[J]. European Journal of Soil Science, 2008, 59(2): 292–303. [6] 姜成晟, 王劲峰, 曹志冬. 地理空间抽样理论研究综述[J]. 地理学报, 2009, 64(3): 368–380. [7] 李连发, 王劲峰. 地理数据空间抽样模型[J]. 自然科学进展, 2002, 12(5): 545–548. [8] 张磊, 朱阿兴, 杨琳, 等. 基于分融策略的土壤采样设计方法[J]. 土壤学报, 2017, 54(5): 1079–1090. [9] 杨琳, 朱阿兴, 李宝林, 等. 应用模糊C均值聚类获取土壤制图所需土壤-环境关系知识的方法研究[J]. 土壤学报, 2007, 44(5): 784–791. [10] 李志斌. 基于地统计学方法和Scorpan模型的土壤有机质空间模拟研究[D]. 北京: 中国农业科学院, 2010. [11] 朱阿兴. 精细数字土壤普查模型与方法[M]. 北京: 科学出版社, 2008. [12] 王劲峰, 武继磊, 孙英君, 等. 空间信息分析技术[J]. 地理研究, 2005, 24(3): 464–472. [13] 张忠启, 于法展, 于东升, 等. 红壤区土壤有机碳时间变异及合理采样点数量研究[J]. 土壤学报, 2016, 53(4): 891–900. [14] 孟斌, 王劲峰. 地理数据尺度转换方法研究进展[J]. 地理学报, 2005, 60(2): 277–288. [15] Brus D J, Jansen M J W, Gruijter J J D. Optimizing two- and three-stage designs for spatial inventories of natural resources by simulated annealing[J]. Environmental and Ecological Statistics, 2002, 9(1): 71–88. [16] van Groenigen J W, Pieters G, Stein A. Optimizing spatial sampling for multivariate contamination in urban areas[J]. Environmetrics, 2000, 11(2): 227–244. [17] Sacks J, Schiller S. Spatial designs//Statistical Decision Theory and Related Topics IV[M]. New York, NY: Springer New York, 1988: 385–399. [18] 康立山. 非数值并行算法(第一册)模拟退火算法 [M]. 北京: 科学出版社, 1994. [19] Metropolis N. Equations of state calculations by fast computing machines[J]. J. Chem. Phys., 1953, 21: 1087– 1091. [20] Kerry R, Oliver M A. Average variograms to guide soil sampling[J]. International Journal of Applied Earth Observation and Geoinformation, 2004, 5(4): 307–325. [21] Vašát R, Heuvelink G B M, Borůvka L. Sampling design optimization for multivariate soil mapping[J]. Geoderma, 2010, 155(3/4): 147–153. [22] Wang J P, Xu Y. Estimating the standard deviation of soil properties with limited samples through the Bayesian approach[J]. Bulletin of Engineering Geology and the Environment, 2015, 74(1): 271–278. [23] Sumfleth K, Duttmann R. Prediction of soil property distribution in paddy soil landscapes using terrain data and satellite information as indicators[J]. Ecological Indicators, 2008, 8(5): 485–501. Study on Optimal Soil Sampling Scale Selection Based on Spatial Simulated Annealing Method WANG Xiaorui1, ZHOU Shenglu2*, XU Cuilan1, SUI Xueyan1, HUANG Xiaoyang3 (1 Land Development and Consolidation Center of Jiangsu Province, Nanjing 210017, China; 2 School of Geography and Ocean Science, Nanjing University, Nanjing 210023, China; 3 Jiangsu Poly Real Estate Development Co., Ltd., Nanjing 210018, China) Four sampling point layouts at different scales based on different grid sizes: scale a, 7 050 sampling points in 0.5 km × 0.5 km; scale b, 1 757 sampling points in 1 km × 1 km; scale c, 444 sampling points in 2 km × 2 km; scale d, 110 sampling points in 4 km × 4 km were set up. Then, the optimized selection of the original soil sampling points at the four sampling scales were conducted using the simulated annealing method, and the optimum sampling numbers of scales a, b, c and d were 956, 751, 283 and 95, respectively, and were uniformly distributed in the space. Relative to the decrease in the sampling scale, the number of sampling points increased multiplicatively, but the predicted accuracy of soil properties did not increase proportionately. With the increased sampling point number, the predicted accuracy of soil properties gradually decreased. Considering the number of samples and the predicted accuracy of soil properties, a sampling scale of 2 km × 2 km is optimal for soil organic matter. Soil sampling scale; Simulated annealing method; Soil organic matter; Prediction of soil properties P934 A 10.13758/j.cnki.tr.2021.01.026 王晓瑞, 周生路, 徐翠兰, 等. 基于空间模拟退火算法的最优土壤采样尺度选择研究. 土壤, 2021, 53(1): 190–196. 江苏省国土资源科技计划项目(2017018、2017019、2018004)资助。 (zhousl@nju.edu.cn) 王晓瑞(1986—),男,甘肃武威人,博士,工程师,主要从事土地整治与土地评价研究。E-mail: 279504502@qq.com2.4 不同尺度土壤有效样点分析
2.5 土壤有机质最佳采样尺度选择
3 结论
