基于分融策略的土壤采样设计方法*

张 磊 朱阿兴 杨 琳 秦承志 刘军志 刘雪琦

（1 南京师范大学地理科学学院，南京 210023）

（2 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室，北京 100101）

（3 虚拟地理环境教育部重点实验室（南京师范大学），江苏省地理环境演化国家重点实验室培育建设点，江苏省地理信息资源开发与利用协同创新中心，南京 210023）

（4 威斯康辛大学麦迪逊分校地理系，WI 53706，美国）

（5 南京大学地理与海洋科学学院，南京 210093）

基于分融策略的土壤采样设计方法*

张 磊1，3朱阿兴1，2，3，4杨 琳2，5†秦承志2刘军志1，3刘雪琦1，3

（1 南京师范大学地理科学学院，南京 210023）

（2 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室，北京 100101）

（3 虚拟地理环境教育部重点实验室（南京师范大学），江苏省地理环境演化国家重点实验室培育建设点，江苏省地理信息资源开发与利用协同创新中心，南京 210023）

（4 威斯康辛大学麦迪逊分校地理系，WI 53706，美国）

（5 南京大学地理与海洋科学学院，南京 210093）

采样设计方法在地理要素空间分布推测中起着关键作用。采集的样点数量尽可能少且推测精度较高通常是采样设计的目标。此外，高效合理的采样方案应保证较高的推测可信度，同时尽可能避免冗余样点。传统的采样方法大多依靠增加样点个数来提高推测精度，且对样点集内部的冗余情况考虑较少。为获取更加高效合理的样点集，在环境条件越相似、地理要素越相似的假设下，通过环境相似度分析计算，得到样点的推测可信度和样点集内部的冗余度，并提出一种基于分融策略的样点设计方法。该方法在分化阶段将推测可信度低的样点进行分化，增加样点以降低推测不确定性，在融合阶段将环境条件过于相似的样点进行融合以降低冗余，通过多次分化融合最终使得推测可信度和冗余度均达到一定的预设标准，得到最佳样点方案。将该方法应用于美国Raffelson研究区的土壤采样，结果表明，该方法在分化阶段可以有效提高样点的推测可信度，在融合阶段能够有效去除冗余样点，最终可得到用于推测的高效样点。将本方法与传统的规则采样和分层随机采样进行对比，结果反映本方法获得的样点在同等数量下推测可信度更高，冗余度更低，更高效。

采样方法；推测可信度；样点冗余度；土壤制图；土壤—环境关系

通过采集样点进行地理要素空间分布推测时，样点的布设方式和数据质量会直接影响最终的推测结果［1-4］。寻找高效、合理的样点设计方法是地理要素空间分布研究的重要环节。由于采样成本的限制，通常希望利用相对较少的样点获得较高精度的推测结果，从而实现高效率的采样目标［5-6］。达到高效采样的目标通常可从两个角度出发：一是尽可能地获取代表性好的样点，从而提高推测精度；二是在允许的精度范围内尽可能减少样点数量，从而节约成本。基于上述两点，高效合理的样点集应在保证一定推测可信度的前提下尽可能避免存在冗余样点，即避免存在属性空间中过度相似的样点。

传统的概率采样（如简单随机采样和规则采样）一般通过增加样点数量来实现推测精度的提高［7-10］。在地理空间域的采样方法中，Brus等［11］采用k均值聚类将地理空间划分成等面积的子区域，以达到地理空间均匀分布的目标，其推测精度的提高仅能通过增加划分子区域个数或增加每个子区域的样点数量实现。利用环境因子辅助数据提高样点推测精度的现有方法主要从样点在环境属性空间的分布出发［12-17］，例如Minasny和McBratney［12］运用拉丁超立方方法，提出一种可以全面覆盖整体环境辅助数据的采样方法；Minasny等［13］提出了基于变差四叉树算法的采样方法，将目标区域根据环境因子的变化复杂程度进行划分，使得每个样点所代表区域内的环境变化幅度相对均衡。这些方法得到的样点在环境属性空间中有着较优的分布，但并未针对所设计的样点集明确地给出一种能够对最终推测精度具有指示作用的参考量，即样点推测可信度，从而可给每个样点的可推测范围和推测的可信度做出提前预判。杨琳等［18］利用环境因子辅助数据，提出了一种寻找典型点的目的性采样方法，该方法采用模糊聚类提取出环境因子相似的不同组合，将环境因子组合的中心位置近似作为典型点的位置，通过寻找典型样点达到减少采样数量的目的。该方法虽然在一定程度上减少了采样数量，但未对典型点之间的冗余程度进行定量表达。

在样点设计的过程中，样点用于地理要素推测时的可信度和样点集内部的冗余度是控制采样精度和成本的重要依据。在这方面有研究者做了探讨，刘京等［19］提出了样点个体代表性的度量方法，Zhang等［20］提出了基于推测不确定性补样方法，此类方法均从待推测点出发，通过环境相似度对推测不确定性做出了度量，但缺少从单个样点自身的角度出发，对其可推测范围及范围内的推测可信度给出定量表达；同时，现有研究缺乏对所设计的样点集内部冗余情况进行定量分析，也缺少对可能存在的过度相似样点做出相应处理。基于地理环境越相似，地理要素属性越相似的基本假设，Zhu［21］提出了土壤环境相似度的度量方法，环境相似度可用来确定样点与待推测点之间的相似度以及样点集内部的相似度，既可反映样点的推测可信度，也可反映样点集内部的冗余程度。基于此，本文提出一种基于分融策略的样点设计方法，可兼顾样点的推测可信度和样点集内部的冗余度，将该方法应用于美国Raffelson研究区的土壤采样，并与传统的规则格网和分层随机方法进行样点推测可信度和冗余度等方面的对比，对该方法的有效性进行验证。

1 数据与研究方法

1.1 研究区及数据

研究区为位于美国威斯康星州La Crosse县东部的Raffelson流域，区域中心位置为43°59′49″N、90°57′46″W，面积大约4 km2。该区为典型的无冰碛作用的山脊―沟谷地形，具有相对平缓的、狭窄的山脊，以及宽平的沟谷。研究区高程在254～416 m，坡度变化范围在0°至60°之间。大部分山顶和河谷利用为耕地，山坡主要为林地，少部分因人类活动被改造为牧场。

依据已有研究［25-26，28］，在该研究区选取了以下7个协同环境因子用于采样设计：高程、坡度、沿剖面曲率、沿等高线曲率、地形湿度指数、地质类型和冲积物成分比例，分辨率均为10 m。该研究区已有土壤类型图如图1所示，该土壤图由SoLIM（Soil Land Inference Model）方法生成［25］，精度为83.8%，被认为是精度较高、较详细的土壤类型图。研究区有99个实际野外采样点，如图1所示，这些样点均已覆盖所有的16种土壤类型。

1.2 基于分融策略的采样设计方法

1.2.1基本思路 基于分融策略的采样设计方法的目标为，提高单个样点推测可信度的同时，尽可能降低样点集内部的冗余度。分融策略包括“分化”和“融合”两个策略。“分化”是为了提高样点对其代表域的推测可信度，将单个样点分化为多个样点，使用这些新样点重新更好地代表原样点的代表域，以多个样点降低原样点在其代表域中较高的推测不确定性，提高其推测可信度。“融合”即当样点集内部存在过度相似的样点时，对此类样点进行融合，去除样点冗余，减少样点数量。最终，该方法通过不断地对样点进行分化和融合，逐步增加、删减样点，逐渐寻找到兼顾推测可信度和冗余度的最合适样点集。

该方法的两个关键概念是：单个样点的推测可信度和样点集内部的冗余度。下面分别介绍这两个关键概念，以及基于分化和融合策略的采样设计方法。

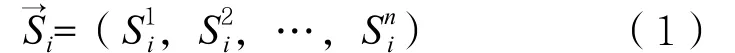
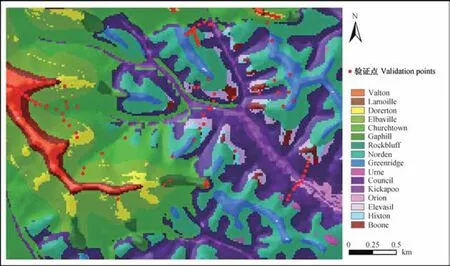
图1 研究区已有土壤图及验证样点Fig. 1 Existing soil map of the studied region and locations of validation points

通过对环境相似度向量的分析，可计算由样点集对待推测点进行推理时产生的不确定性Ui［22］。

式中，如果待推测点i与对其代表性最好（即环境最相似）的样点之间的环境相似度较低，那么，用现有样点推测待推测点的土壤属性值将会有较高的不确定性。该不确定性计算方法已在现有研究中证实有效［23-24］，即推测不确定性与预测残差之间存在正相关，推测不确定性对预测精度具有重要的指示作用。

此外，单个样点的推测可信度不能仅考虑代表域中所有待推测点的不确定性总和，也要考虑代表域的范围大小，也就是代表域中待推测点的数量。代表域是研究区中与某一样点在环境要素上最相似的区域，也就是该样点可推测的地理空间范围，样点的代表域可以使用如下的集合表达式来描述：

式中，Zk为样点k的代表域，代表域是由待推测点集表达，点集中每一个待推测点i均属于待推测点全集Z，且每一个待推测点i都满足等式Max（→Si）=Sk，Max（→S）是环境相似度与待推测点i最大的样

ii点相似度值；Ski为样点k与待推测点i之间的环境相似度值，即待推测点i与对其代表性最好（即环境最相似）的样点为样点k，满足这样条件的待推测点集则为样点k的代表域。

综合推测不确定性与代表域，单个样点的推测可信度可由如下公式表达：

（2）样点集内部冗余度：设计合理的样点集在其内部应当不存在过于相似的子样点集。为了去除这些过相似的冗余样点，需要计算样点集内所有样点之间的相似度，判断样点集中是否存在过相似现象。

式中，R为样点集内部的冗余度，通过所有的样点对中的最大相似度值表达；n为样点集中样点的总个数，Sji为第i个样点与第j个样点的相似度（i≠j），将样点集内每对样点之间进行相似度计算，若最大相似度值过高，则可视为该样点集中存在过相似现象，也就导致了样点设计的冗余。

1.2.3样点设计方法 方法的总体流程如图2所示。样点的设计过程主要如下：

（1）设置初始样点集，可采用简单随机采样的方式。

（2）计算每个样点的推测可信度。

（3）找到推测可信度最低的样点，若其推测可信度不大于预设阈值，则分化该样点，生成新样点集，并重复步骤（3）；否则至步骤（4）。分化策略：首先需要确定分化域，分化域是样点集中推测可信度最低的样点的代表域，在分化域中重新找到若干个新样点（数量大于1）来替换原样点集中推测可信度最低的样点，这些新样点即为分化样点集。可通过随机抽样的方式，反复在分化域中抽取不同的样点集，选取将分化域中的推测不确定性降低程度最大的作为分化样点集，最后将分化前推测可信度最低的样点从当前的全样点集中去除，并将分化样点集加入当前的全样点集中。

（4）确定样点集内部的冗余度，若冗余度不小于阈值，则融合过相似样点，生成新样点集，并重复步骤（4）；否则至步骤（5）。融合策略：首先需要确定融合域，融合域是多个过相似冗余样点的代表域之和，在融合域中重新找到一个新样点来替换原先的冗余样点。可从融合域中反复随机抽取不同的单个样点，选取使得融合域中推测不确定性最小的作为融合样点，将融合前的冗余样点从当前的全样点集中去除，并将融合样点加入当前的全样点集中。

（5）重复步骤（2）～（4），直至推测可信度和冗余度同时达到阈值要求，则结束。

该方法需设置两个参数：分化条件中最低推测可信度的阈值和融合条件中最高冗余度的阈值。

1.3 方法评价

为验证本文所提采样方法的有效性，从三个方面对其进行评价。首先，需验证所计算的样点推测可信度是否对推测精度具有指示作用。为此，从研究区随机抽取不同数量（10、11、12、…、30）的样点，计算样点的代表域和推测可信度。假设已有土壤图为真实的土壤类型分布情况，从已有土壤图中得到每个样点的土壤类型，利用这些样点推测研究区的土壤类型，即将落入某样点代表域内的样点均赋为该样点的土壤类型。将99个野外样点作为验证点，计算利用抽取样点进行推测的推测精度。由于各样点的代表域内包含的验证样点数量不同，仅当代表域中验证样点数量大于或等于5个时，可用来计算推测精度。从而得到不同推测可信度样点所对应的推测精度。

其次，需验证该方法在分融过程中是否能够有效提高推测可信度且降低冗余度。使用本文提出的样点分融法进行样点设计，设置样点推测可信度阈值和样点集冗余度阈值，查看迭代过程中样点数量、推测可信度和冗余度等数值的变化情况。

最后，将基于分融策略的采样方法与其他常用统计采样方法（规则格网和分层随机方法）进行以下两方面对比，一是随样点数量增加，推测可信度和冗余度的变化，二是相同数量样点下生成的土壤类型图的不同。设定3组不同数量（15、20和25），采用三种采样方法设计样点，其中规则格网样点按照5×3、5×4、5×5设计，分层随机采样以母质分层。制图方法采用SoLIM方法［25］。

1.4 方法的参数敏感性分析

该方法的两个重要参数——最低推测可信度和最高冗余度对结果具有较大影响，有必要对这两个参数的敏感性进行分析。由于同时变化两个参数不便于最终结果的表达，并且若最低推测可信度设置过高或最高冗余度设置过低会导致无法得到有效结果，因此，分别将其中一个参数固定为一个较为合理的数值，再分析样点数量随另一个参数的变化情况。该分析为使用本方法的参数设置提供了参考依据。

2 结 果

将基于分融策略的采样方法应用于研究区，从三个方面对该方法进行评价，并进行了参数敏感性分析，研究结果如下：

图2 方法流程图Fig. 2 Flow chart of the method

图3 推测可信度与验证精度之间的关系散点图Fig. 3 Scatter plot of prediction reliability vs. validation accuracy

2.1 样点推测可信度与推测精度的关系

为验证所计算的样点推测可信度是否对推测精度具有指示作用，得到不同推测可信度样点的推测精度。二者之间关系如图3所示，可以看出，单个样点的推测可信度与实际的验证精度具有较高的相关性（相关系数为0.915），对推测结果具有较好的指示作用。因此，以提高推测可信度作为采样设计的主要目标是合理的。

2.2 样点数量、推测可信度与冗余度变化

为验证该方法在分融过程中是否能够有效提高推测可信度且降低冗余度，使用本文提出的样点分融法进行样点设计，设置最低需要满足的样点推测可信度阈值为0.86，最高的样点集冗余度阈值为0.80。

本方法所设计的样点数量的变化如图4所示。随着迭代次数的增加，先通过样点分化不断提高了样点数量，在迭代次数为22之后，由于分化产生的样点开始集中出现过相似的冗余样点，继而开始进行样点融合，样点数量开始减少，在减少至无冗余之后，由于样点的推测可信度有所下降，再次开始分化样点。因此，如图4所示，样点数量发生了多次反复的上升和下降，并最后稳定在一定合理的数目，本研究中为25个。

在迭代过程中，所有样点推测可信度的均值、最大值和最小值的演变情况如图5所示。可以看出，分融方法在前期很大程度上提高了样点的推测可信度，并最后保证了所有样点的推测可信度均达到0.86以上。

图6以迭代次数从22至29为例，反映了在去除过相似样点的过程中，样点集内部冗余度和所有样点平均推测可信度的变化情况。可以发现，随着过相似冗余样点的去除，样点数量从27减少至20，样点集的冗余度从0.894降低至0.793，样点的平均推测可信度仅从0.883降至0.872。因此，在融合过程中，冗余度明显降低，且推测可信度并未受到较大影响，体现了融合策略的有效性。

在分融过程中，最终得到的平均推测可信度并非是所有迭代过程中的最大值。例如，在第37次迭代中，样点的平均推测可信度达到了最高值0.887，在最后迭代结束时，平均推测可信度为0.883，样点数量仅为25，但第37次迭代中产生的样点数量为28。因此，综合推测精度与采样成本考虑，最终产生的25个样点设计更为高效合理。

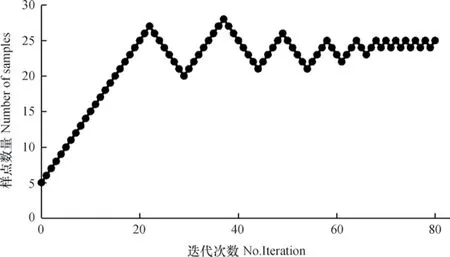
图4 样点数量的变化过程Fig. 4 Variation of the number of sampling sites with iteration

图5 样点推测可信度的变化过程Fig. 5 Variation of the prediction reliability of the sampling sites with iteration

图6 融合过程中（迭代次数从22至29）冗余度（a）和推测可信度（b）的变化Fig. 6 Variation of redundancy（a）and prediction reliability（b）in the fusion procedure（iteration from 22 to 29）

2.3 基于分融策略的采样方法与其他方法的对比

基于分融策略所设计的样点、规则格网设计的样点和分层随机（以母质分层）样点的分布情况（样点数量为20时）如图7（a）所示。三种方法所设计的样点在空间上的分布存在很大的不同。分层随机样点较易出现样点聚集情况，基于分融策略所设计的样点在空间上的分布较均匀，基本覆盖了各种地形部位。

三种采样方法所得采样点的平均推测可信度、最低推测可信度和冗余度如表1所示，每组数量的样点进行100次重复实验，并求得重复实验结果的均值。在不同样点数量的情况下，基于样点分融方法所获取的样点的平均推测可信度均高于规则格网和分层随机方法，最低推测可信度远高于规则格网和分层随机方法，且样点数量较小时，基于分融策略的采样方法也保持了较高的最低推测可信度。也就是说，基于分融策略的采样方法可以保证每个所选样点均具有较高的推测可信度，且不受样点数量影响、比较稳定，而分层随机或规则采样方法则有可能采集到推测可信度较低的样点，例如规则采样和分层随机采样在样点数量为15时的100次实验最低推测可信度变化范围分别为0.662～0.793和0.651～0.764。在样点内部的冗余度方面，其余两种方法均存在冗余度较高的情况，而本文提出的方法较好地避免了样点冗余的现象，且随着样点增加，冗余度逐渐降低。这表明了基于分融策略的采样方法的高效性。而规则采样法和分层随机采样法由于缺少能控制样点集内部冗余度的指标，导致了随样点数量的增加，冗余度有一定的提高。

三种方法的推理制图结果分别如图7（b）、7（c）和7（d）所示（样点数量均为25）。总体而言，基于分融策略的采样样点所得的土壤图较另外两种采样样点所得土壤图具有与原图更高的一致性。基于分融策略的样点覆盖了原图中的15种土壤类型，仅有一种在原图面积中仅占0.23%的土壤类型Urne未覆盖到。尽管图7（b）分布在研究区东部比较窄的凸背坡上的几种小面积土壤类型Elevasil、Hixton和Boone出现了错分，但较另外两个土壤图要准确，此外，也存在对土壤类型Orion推测面积过大的问题。规则采样样点和分层随机样点分别仅覆盖到8种和12种土壤类型，所生成的土壤图均对研究区西部山坡上土壤类型的分布刻画较差，体现在土壤类型Lamoille的缺失及土壤类型Dorerton的错分；同时，基于分层随机样点所生成土壤图中将土壤类型Elevasil错分为Hixton，土壤类型Orion也存在推测面积过大的问题。此外，由于规则采样样点未覆盖到一种母质而导致存在无推测值的区域，见图7（c）中灰白色NoData区。

2.4 参数敏感性

对方法的两个重要参数——最低推测可信度和最高冗余度进行敏感性分析，分别将其中一个参数固定为一个较为合理的数值，再分析样点数量随另一个参数的变化情况。将最高冗余度阈值设定为0.80，最低推测可信度阈值分别设置为0.70、0.75、0.80和0.85（最低推测可信度阈值大于0.87难以得到有效结果，因此最高设为0.85），计算采用所提出方法得出最佳样点数量。此外，将最低推测可信度阈值固定为0.87，将最高冗余度阈值分别设置为0.80、0.85、0.90和0.95（最高冗余度阈值小于0.80难以得到有效结果，因此最低设为0.80），计算采用所提出方法得到最佳样点数量。

图7 三种采样方法对比：（a）三种不同类型采样点的位置分布；（b）、（c）和（d）依次为样点数量为25时基于分融策略的采样、规则采样和分层随机采样样点所得推理制图结果Fig. 7 Comparison of three sampling methods：（a）Locations of the sampling sites relative to sampling method in the study area；The predicted map from three different sampling method using 25 sample points：（b）from sampling based differentiation and fusion strategy；（c）from grid sampling method；（d）from stratified random sampling method

表1 三种不同方法所得采样点的平均推测可信度、最低推测可信度和冗余度Table 1 Mean and minimal prediction reliability and redundancy relative to sampling strategy

上述两种设置所得结果如图8所示。可以看出，在最高冗余度不变的情况下，随着最低推测可信度的增加，分融法的最佳样点数量增加，当最低推测可信度低于0.80时，样点数量受最低推测可信度阈值的影响很小，从0.80至0.85时，样点数量显著增加，即当最低推测可信度增加至一定值，则需要更多的样点。此外，在推测可信度保持不变的情况下，当最高冗余度从0.80至0.85时，样点数量增加显著，此时最高冗余度起到了调节样点数量的效果，当最高冗余度高于0.85时，样点数量保持稳定在34～35之间，即最高冗余度增加至一定的值，则不再需要更多的样点。

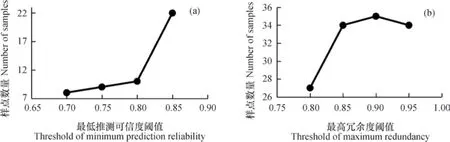
图8 样点数量随最低推测可信度阈值（a）和最高冗余度阈值（b）的变化Fig. 8 Variation of the number of sampling sites with threshold of prediction reliability（a）and threshold of redundancy（b）

3 讨 论

样点推测可信度和样点集冗余度是基于分融策略采样方法的重要概念，这两者对推测精度和采样成本具有指示作用，即样点推测可信度越高，推测精度越高；样点集冗余度越高，成本越高。一般在样点数量不变的情况下，样点推测可信度越高，样点集冗余度会越低，反之亦然。二者之间存在矛盾且统一的关系，本文通过分融策略试图解决二者之间的矛盾，在初期样点数量增加的情况下，分化起主导作用，推测可信度得以提高，但后期样点增加会产生冗余样点，此时通过融合策略逐渐去除冗余样点。最终找到兼顾高推测可信度和低冗余度的样点集。

基于分融策略的采样方法，初期由于分化过程占主导地位，大幅度提高了推测可信度，样点数量较少；在后期，样点数量逐渐增多，推测可信度已满足了阈值条件，融合过程开始占据主导地位，其目标为降低样点集内部的冗余，通过将过度相似的样点融合，重新找到一个新样点替代原来的多个冗余样点的方式实现。因此，相比于规则采样和分层随机采样，基于分融策略的采样方法必然会得到冗余度更低的样点集，这也是基于分融策略这种采样方法的优点。而与之不同的是，规则采样法和分层随机采样法则由于缺少一个指标能控制样点集内部的冗余度，导致了在样点数量增加的过程中冗余度有一定的提高的现象。

对应样点推测可信度和样点集冗余度，本方法有两个需设定的重要阈值参数——最低推测可信度和最高冗余度。一般而言，最低推测可信度阈值越高，推测精度越高，但样点数量也会增加，即成本上升；最高冗余度阈值设定越低，样点间的相似度越小，样点数量减少，但也限制了推测可信度的提高。有时，推测可信度阈值设定过高同时冗余度阈值设定过低，可能样点设计无解，即无法得到同时满足两个参数的样点，如本文案例中分别设置为0.90和0.60时。因此，设定这两个参数成为推测精度和采样成本的平衡问题。

在实际应用本文所提采样方法时，不同的研究区存在不同的阈值设定方案，用户可设定几组阈值进行多次实验进而选择适宜的参数。若预算充足允许采集更多的样点，在最高冗余度阈值不变的情况下，可适当提高最低推测可信度阈值，以提高推测精度。若预算有限，在保证一定最低推测可信度的情况下，可适当减小最高冗余度阈值以减少样点数量。后续工作中将会对有关阈值的设置进行更深入的分析，例如使用多个研究区进行应用来寻找规律。

4 结 论

本文提出了一种基于分融策略的采样设计方法，通过分融策略寻找到推测可信度高且冗余度小的高效样点集。以Raffelson研究区为例，结果表明，本文提出的样点推测可信度与推测精度成正相关关系，说明样点的推测可信度对推测结果具有较好的指示作用。该方法在样点分化的过程中提高了样点的推测可信度，同时，样点融合去除了冗余样点，且去除冗余样点对推测可信度的影响很小，达到了在推测可信度保持稳定的情况下尽可能减少样点数量的目标。该方法与传统的规则格网和分层随机采样方法对比，可获取推测可信度更高且冗余度更低的样点，采集到的样点更为高效，生成土壤类型图更为准确。此外，本文还对方法的两个重要参数（最低推测可信度和最高冗余度）进行了敏感性分析，为采用本方法进行参数设置提供了初步参考依据，后续工作还包括将该方法用于实际土壤采样制图中以进一步验证该方法的有效性，以及方法参数与土壤制图精度的关系等。

［1］ Brus D J，Gruijter J J D. Random sampling or geostatistical modelling? Choosing between designbased and model-based sampling strategies for soil.Geoderma，1997，80（1/2）：1—44

［2］ Gregoire T G，Valentine H T. Sampling strategies for natural resources and the environment. International Journal of Environmental Analytical Chemistry，2008，88（8）：596—597

［3］ Mcbratney A B，Santos M L M，Minasny B. On digital soil mapping. Geoderma，2003，117（1/2）：3—52

［4］ Stein A，Ettema C. An overview of spatial sampling procedures and experimental design of spatial studies for ecosystem comparisons. Agriculture Ecosystems &Environment，2003，94（1）：31—47

［5］ Hartemink A E ，Mcbratney A，Mendonça-Santos M D L. Digital soil mapping with limited data. New York：Springer-Verlag，2008

［6］ 朱阿兴，李宝林，裴韬，等. 精细数字土壤普查模型与方法. 北京：科学出版社，2008 Zhu A X，Li B L，Pei T，et al. Model and method of detail digital soil survey（In Chinese）. Beijing：Science Press，2008

［7］ Cochran W G. Sampling techniques，3rd ed. New York：John Wiley & Sons，1977

［8］ Kish L. Survey sampling. New York：John Wiley &Sons，1985

［9］ Webster R，Oliver M A. Statistical methods in soil and land resource survey. Oxford：Oxford University Press，1990

［10］ Mcbratney A B，Webster R. How many observations are needed for regional estimation of soil properties? Soil Science，1983，135（3）：177—183

［11］ Brus D J，Gruijter J J，Groenigen J W. Designing spatial coverage samples using the k-means clustering algorithm// Digital soil mapping. An introductory perspective. New York：Elsevier，2006：183—192

［12］ Minasny B，McBratney A B. A conditioned Latin hypercube method for sampling in the presence of ancillary information. Computers & Geosciences，2006，32（9）：1378—1388

［13］ Minasny B，McBratney A B，Walvoort D J J. The variance quadtree algorithm：Use for spatial sampling design. Computers & Geosciences，2007，33（3）：383—392

［14］ Simbahan G C，Dobermann A. Sampling optimization based on secondary information and its utilization in soil carbon mapping. Geoderma，2006，133（3/4）：345—362

［15］ Brus D J，Heuvelink G B M. Optimization of sample patterns for universal kriging of environmental variables.Geoderma，2007，138（1/2）：86—95

［16］ Zhu A，Yang L，Li B L，et al. Construction of membership functions for predictive soil mapping under fuzzy logic. Geoderma，2010，155（3/4）：164—174

［17］ Qin C Z，Zhu A X，Qiu W L，et al. Mapping soil organic matter in small low-relief catchments using fuzzy slope position information. Geoderma，2012，171/172（2）：64—74

［18］ 杨琳，朱阿兴，秦承志，等. 基于典型点的目的性采样设计方法及其在土壤制图中的应用. 地理科学进展，2010，29（3）：279—286 Yang L，Zhu A X，Qin C Z，et al. A purposive sampling design method based on typical points and its application in soil mapping（In Chinese）. Progress in Geography，2010，29（3）：279—286

［19］ 刘京，朱阿兴，张淑杰，等. 基于样点个体代表性的大尺度土壤属性制图方法. 土壤学报，2013，50（1）：12—20 Liu J，Zhu A X，Zhang S J，et al. Mapping soil properties using individual representativeness of samples over large area（In Chinese）. Acta Pedologica Sinica，2013，50（1）：12—20

［20］ Zhang S J，Zhu A X，Liu J，et al. An heuristic uncertainty directed field sampling design for digital soil mapping. Geoderma，2016，267：123—136

［21］ Zhu A X. A similarity model for representing soil spatial information. Geoderma，1997，77（2/4）：217—242

［22］ Zhu A X，Band L E，Dutton B，et al. Automated soil inference under fuzzy logic. Ecological Modelling，1996，90（2）：123—145

［23］ Zhu A X. Measuring uncertainty in class assignment for natural resource maps under fuzzy logic.Photogrammetric Engineering & Remote Sensing，1997，63（10）：1195—1202

［24］ Zhu A X，Liu J，Du F，et al. Predictive soil mapping with limited sample data. European Journal of Soil Science，2015，66（3）：535—547

［25］ Zhu A X，Hudson B，Burt J，et al. Soil mapping using GIS，expert knowledge，and fuzzy logic. Soil Science Society of America Journal，2001，65（5）：1463—1472

［26］ Qi F，Zhu A. Knowledge discovery from soil maps using inductive learning. International Journal of Geographical Information Science，2003，17（8）：771—795

［27］ Zhu A，Band L E. A knowledge-based approach to data integration for soil mapping. Canadian Journal of Remote Sensing，1994，20（4）：408—418

［28］ 朱阿兴，李宝林，杨琳，等. 基于GIS、模糊逻辑和专家知识的土壤制图及其在中国应用前景. 土壤学报，2005，42（5）：844—851 Zhu A X，Li B L，Yang L，et al. Predictive soil mapping based on a GIS，expert knowledge，and fuzzy logic framework and its application prospects in China（In Chinese）. Acta Pedologica Sinica，2005，42（5）：844—851

A Sample Differentiation and Fusion Strategy for Designing of Soil Sampling

ZHANG Lei1，3ZHU A-Xing1，2，3，4YANG Lin2，5†QIN Chengzhi2LIU Junzhi1，3LIU Xueqi1，3
（1School of Geographical Science，Nanjing Normal University，Nanjing210023，China）
（2State Key Laboratory of Environment and Resources Information System，Institute of Geographical Sciences and Resources
Research，Chinese Academy of Sciences，Beijing100101，China）
（3Key Laboratory of Virtual Geographic Environment（Nanjing Normal University），Ministry of Education；State Key Laboratory Cultivation Base of Geographical Environment Evolution（Jiangsu Province）；Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application，Nanjing210023，China）
（4Department of Geography，University of Wisconsin-Madison，Madison，WI53706，USA）
（5School of Geographic and Oceanographic Sciences，Nanjing University，Nanjing210093，China）

【Objective】Quality of mapping based on prediction of geographic variables is greatly affected by the layout of the sampling sites. Due to the limitation of sampling cost，it is generally expected to have fewer sampling sites that will be able to provide more information for accurate prediction. To achieve such a target of efficient sampling，it is advisable to proceed from the following two point：first，set up sampling sites that are highly representative of the area of interest for better prediction accuracy，and second，reduce the number of sampling sites as many as possible without risking any loss of required accuracy. Based on the assumption that the more similar the two sites in geographic environment，the more similar their geographic elements，it is held that every sampling site can be used to represent an area similar to the site in environment，and the similarity between the sampling site and the sites to be predicted can be used to determine reliability of the prediction，meanwhile，the similarity within the sampling site set can be used to determine redundancy of the sampling site set. So，the layout of efficient sampling sites needs to keep balance between reliability of the prediction and redundancy of the sampling site set. 【Method】 In this paper，a sample differentiation and fusion strategy is set forth for designing of sampling. The differentiation strategy is to increase the number of sampling sites so as to improve reliability of later on predictions，while the fusion strategy is to merge over-similar sampling sites，so as to reduce redundancy of the sampling site set. Through repeated differentiation and fusion，a preset requirement is finally met for prediction reliability and sampling site redundancy. The method has been tested in a case study of a small watershed in Raffelson，Wisconsin of USA. First，a comparative analysis was done of sampling sites varying in prediction reliability with 99 validation sampling sites to determine relationship between prediction reliability and validation accuracy.Then，verification was performed of effectiveness of the proposed strategy improving prediction reliability in its first phase and reducing redundancy of the sampling site set in its second phase. And in the end，comparison was done of the proposed method in this paper with other sampling methods（grid sampling and stratified simple random sampling）using the same number of sampling sites（15，20 and 25，separately）.【Result】Results show that prediction reliability is positively related to prediction accuracy，so the former can be used as a better indicator of the latter. From the specific processes of the strategy，it can be discerned that，the differentiation can effectively raise the prediction reliability，while the fusion reduce the redundancy of the sampling site set，and what is more，have little impact on the prediction reliability. The comparisons show that the proposed method is higher in prediction reliability and lower in redundancy，and is 17.3%（n=15），14.8%（n=20）and 16.2%（n=25）lower than the grid sampling method，and 16.5%（n=15），15.3%（n=20）and 17.0%（n=25）higher than the stratified simple random sampling method in lowest prediction reliability，respectively，while 8.8%（n=15），12.8%（n=20）and 20.3%（n=25）lower than the grid sampling method，and 6.4%（n=15），12.4%（n=20）and 19.6%（n=25）lower than the stratified simple random sampling method，respectively，in redundancy. 【Conclusion】Therefore，it can be concluded that the proposed method provides a means for obtaining a high prediction reliability and low sampling redundancy in sampling，and hence is a more efficient method for designing sampling schemes than the grid sampling and stratified simple random sampling methods.

Sampling method；Prediction reliability；Sampling redundancy；Soil mapping；Soilenvironmental relationships

P934

A

10.11766/trxb201701030562

* 国家自然科学基金项目（41431177，41471178，41530749）、江苏省高校自然科学研究重大项目（14KJA170001）和国家重点基础研究发展计划（973）项目（2015CB954102）Supported by the National Natural Science Foundation of China（Nos.41431177 and 41471178，41530749），the Natural Science Research Program of Jiangsu Province（No.14KJA170001）and the National Basic Research Program of China（973 Program）（No.2015CB954102）

† 通讯作者 Corresponding author，E-mail：yanglin@ lreis.ac.cn

张 磊（1992—），男，江苏南京人，硕士研究生，研究方向为地理统计学与地理空间采样方法。E-mail：zlxy9892@163.com

2017-01-03；

2017-02-10；优先数字出版日期（www.cnki.net）：2017-03-17

（责任编辑：陈荣府）