矩阵的半正定因子及次酉极因子的扰动界
2016-07-31孔祥强
孔祥强
(菏泽学院 数学系,山东 菏泽 274015)
矩阵的半正定因子及次酉极因子的扰动界
孔祥强
(菏泽学院 数学系,山东 菏泽 274015)
在矩阵的扰动分析中,广义极分解和奇异值分解占有非常重要的地位。对矩阵进行广义极分解,得到半正定因子和次酉极因子。利用矩阵的奇异值分解和广义极分解,得到了范数意义下矩阵的半正定因子和次酉极因子的扰动界,且扰动界是以恒等式的形式给出。
半正定因子;次酉极因子;扰动;广义极分解
矩阵广义极分解中因子的扰动问题是矩阵扰动的重要研究对象。很多学者给出了半正定因子和次酉极因子的扰动界,见文[5]、[6]、[7],这些扰动界都是以不等式的形式给出的。文章从矩阵分解的角度出发,给出了半正定因子及次酉极因子的等式形式的扰动界。
1 几个定义和引理
定义1[1]若矩阵A∈Cn×n,满足AHA=I,则称A为酉矩阵。
定义2[2]若矩阵A∈Cm×n,且满足Ax2=x2,则称A为次酉矩阵。
定义3[2]若矩阵A∈Cm×n,且有分解A=QH,若Q∈Cm×n为酉矩阵,H∈Cn×n为半正定矩阵,称该分解为矩阵A的极分解;若Q∈Cm×n为次酉矩阵,H∈Cn×n为半正定矩阵,称该分解为矩阵A的广义极分解。
定义4[3]设A=(a)∈Cm×n,令A=∑|a|2,称它为矩阵A的F-范数。令A=λ(AHA),称它为矩阵A的2-范数或谱范数。
引理1[4]设矩阵A∈Cm×n,且A=QH,若满足条件R(QH)=R(H),则A的广义极分解因子Q和H是唯一确定的。
2 主要结论

证明 A的奇异值分解为

其中


记T≜A-A,则

两边取共轭转置得

式(2)两边同时左乘N∼H1,右乘M1,得
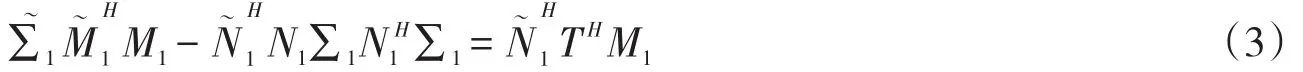
式(1)两边同时左乘M∼H1,右乘N1,得

式(1)两边同时左乘M∼H1,右乘N2,得

式(1)两边同时左乘M2H,右乘N∼1,得

上式两边左乘M∼2H,右乘N1,得
由式(1)得

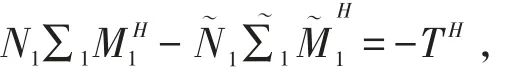

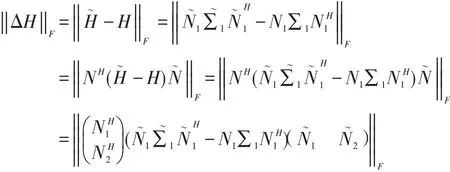

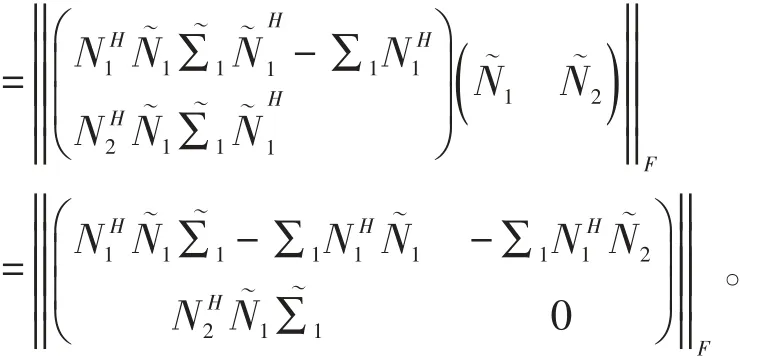
由式(5)知
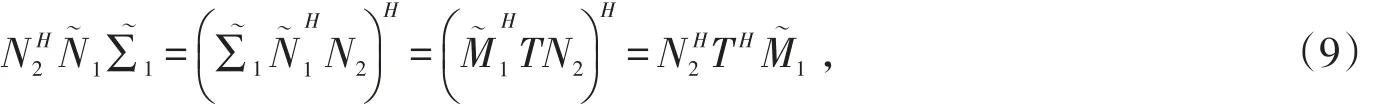
由式(8)知

又

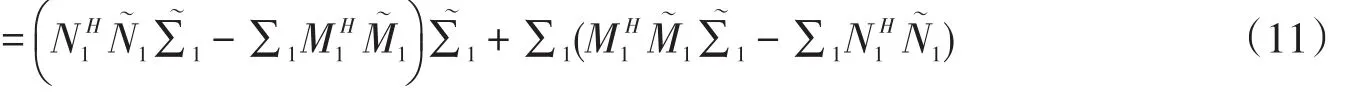
式(3)两边同时取共轭转置得

式(4)两边同时取共轭转置得

将式(12)、式(13)代入式(11)中,得
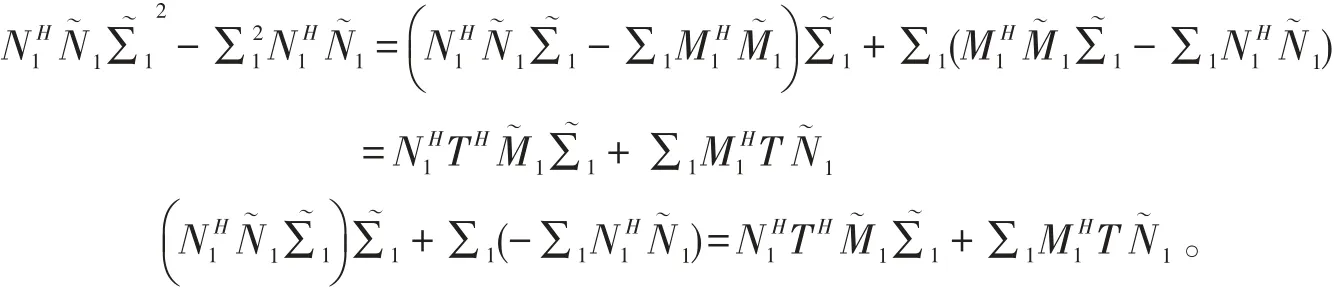
故
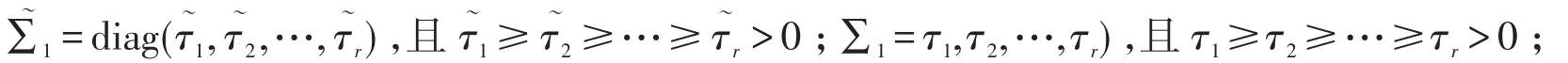
则

即

所以
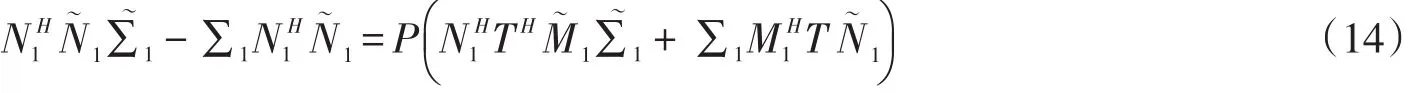
由式(9)、式(10)、式(14)知
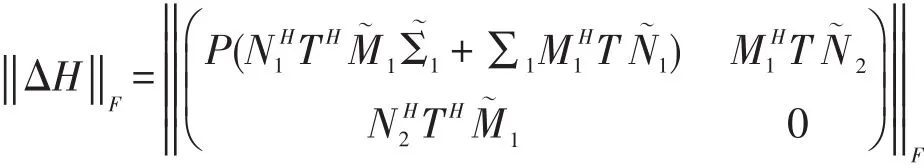
推论1当r=n 定理2条件同定理1,Q∼-Q≜ΔQ,则 由式(6)得 由式(8)得 故 由式(3)、式(4)得 式(17)+式(18)得 故 所以 则 由式(15)、式(16)、式(19)知 推论2当r=n 文章讨论了矩阵广义极分解意义下因子的扰动界问题,在先前学者给出不等式扰动界的基础上,利用矩阵的分解和矩阵的计算,得到了半正定因子的扰动界等式和次酉极因子的扰动界等式。 [1]蒋正新,施国梁.矩阵理论及其应用[M].北京:北京航空学院出版社,1998:95-99. [2]孙继广,陈春晖.广义极分解[J].计算数学,1989,11(3):262-273. [3]孙继广.矩阵扰动分析[M].北京:科学出版社,2001:10-226. [4]Ben-Israel A.,Greville T..Generalized Inverses:Theory and Applications[M].New York,1974:252. [5]ArakiH.,YamagamiS.An inequality for Hilbert-SchmidtNorm[J].Comn.Math.Phys.,1981,81(1):89-96. [6]刘新国.Sylvester方程在矩阵扰动分析中的应用[J].计算数学,1992,14(3):266-273. [7]X Chen,W.Li.Variations for the Q-and H-factors in the Polar Decomposition[J].Calcolo,2008,45(1):99-109. Perturbation Bounds for the Semi-definite Factors and Subunitary Polar Factors KONG Xiang-qiang The generalized polar decomposition and singular value decomposition play a very important role in the analysis of the perturbation of thematrix.The positive semidefinite factor and the sub unitary polar factor are obtained through the generalized polar decomposition of thematrix.By using the singular value decomposition and the generalized polar decomposition ofmatrix,obtained the perturbation bounds for the semi-definite factor and the subunitary polar factor in the sense of F-norm,and the perturbation boundsare given in the form of the identities. Semi-definite factor;Subunitary polar factor;Perturbation;Generalized polardecomposition O241.6 A 1008-9659(2016)02-0063-04 2016-02-24 2015年山东省教育科学“十二五”规划“高等教育数学教学专项”重点资助项目(ZBS15004);2015年菏泽学院教学改革重点课题项目(201510)。 孔祥强(1983-),男,山东菏泽人,讲师,硕士研究生,主要从事应用数学方向研究。

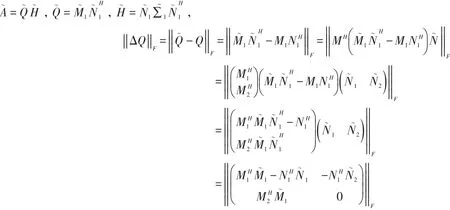

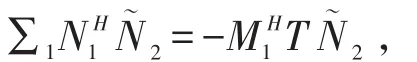






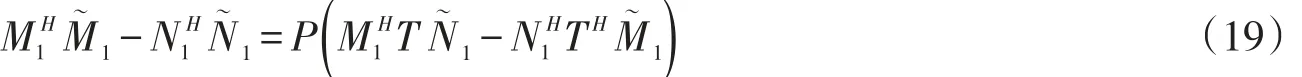
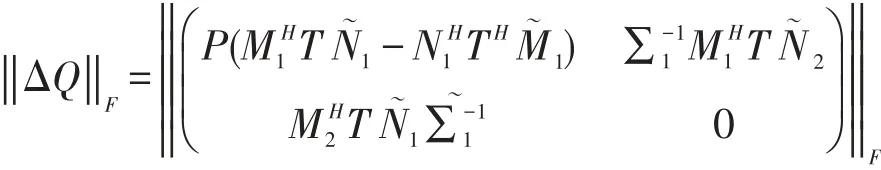
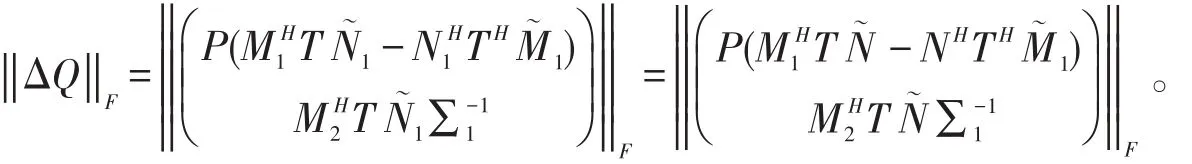
3 结束语
(DepartmentofM athematics,Heze University,Heze,Shandong,274015,China)
