直角三角形台球系统的符号动力学分析
2016-07-31黄俊翔路俊哲
黄俊翔, 路俊哲, 赵 鸿*
(1.厦门大学 物理系,福建 厦门 361005;2.新疆师范大学 物理与电子工程学院,新疆 乌鲁木齐 830054)
直角三角形台球系统的符号动力学分析
黄俊翔1, 路俊哲2, 赵 鸿1*
(1.厦门大学 物理系,福建 厦门 361005;2.新疆师范大学 物理与电子工程学院,新疆 乌鲁木齐 830054)
文章建立直角三角形台球系统的符号动力学描述。通过把直角三角形台球桌内台球运动的方程化简成二维分片映射,得到了相平面上的分割线,从而正、逆映射的分叶线分别被赋予了正、逆向单边无穷符号序列,建立了相空间轨道和符号序列空间的对应。引入度规后,符号空间转化为符号平面,并在符号平面上定义了基本禁止区,初步分析了系统的动力学行为。
三角形台球系统;符号动力学;遍历性
遍历性是统计物理学的基本假设,这一假设对什么样的具体系统能够被满足至今依然没有很好地理解。台球系统(billiard)虽然简单但却非平庸,一直以来作为研究遍历性问题的理想模型而受到广泛的关注[1-8]。一般认为,台球系统具有很好的遍历性,这一点在一般的多边形台球系统模型情况下已经被严格证明。然而当退化到简单的直角三角形台球后,意外地发现这个特例下遍历性可能不能被满足,这一点首先由G.Casati和T. Prosen在研究一般三角形台球时被意识到[1],后来被直接的数值计算所证实[2],并被解析分析初步证明[3]。不仅如此,直角三角台球系统的动力学与一维盒子中两个不等质量的刚性小球系统的碰撞动力学等价,而后者对理解一维硬球气体系统有重要的启示作用。因此直角三角形台球系统值得进一步的深入研究。
直角三角形台球系统具体指一个弹球在直角三角形的台球桌内的无摩擦无能量损耗的无限时间运动,其动力学可以表示成一个二维分片映射[3],以下简称台球映射。依靠数值方法或解析分析,直角三角形台球研究已经积累了丰富的成果[1-8].然而,其对称性特征还没有被系统地研究和描述,而这些对称性特征对于理解系统动力学行为,特别是非遍历性质,具有非常关键的作用。将建立台球映射的符号动力学描述[9],通过构造符号平面及其基本禁止区(basic forbidden zone),利用允字条件初步分析系统的动力学行为,讨论如何在给定参数下应用符号动力学求解该系统可能的周期轨道。

图1 直角三角形台球映射像平面分区
1 直角三角形台球映射
直角三角形台球映射是定义在R×[0,1]上的二维映射,可表示为:
当轨道点属于L区(xi<0,yi>1+xi)时

当轨道点属于M区(-1≤xi≤1,xi≤yi≤1+xi)时;

当轨道点属于R区(xi>0,yi 其中b∈(-2,2)为控制参数。与之对应的逆映射为: 当轨道点属于L-1区(xi+1>b,yi+1>1+b-xi+1)时: 当轨道点属于M-1区(b-1≤xi+1≤b+1,b-xi+1≤yi≤1+b-yi+1)时: 当轨道点属于R-1区(xi+1 图1给出x-y平面上正、逆映射所对应的分区。正映射分区边界由实线表示,逆映射分区边界由虚线表示。可以看出,正、逆映射所对应的分区关于x=b/2对称。给定任一初值点,可以由正、逆映射计算出其将来的和以前的相空间轨道,进而根据轨道点所属分区,可以得到所对应的符号序列,…siˉ…s2ˉs1ˉ∙s1s2…si…,其中∙表示当前位置。如果定义移位操作σ:则在符号序列组成的空间上定义了动力学,从而建立了相空间动力学的符号动力学对应。 从正映射的表达式可以看到,如果一段直线落在某个片区内部,那么这段直线的像一定也是直线,这样一来,一个特定的正向符号序列∙s1s2…sn…,对应相空间的一条线段,整个相空间可以由这些被赋予特定符号序列的线段取代,这些线段叫作相空间的分页线(foliation)。图2给出了部分M区正向符号序列分叶线的分布和形态。同样地,逆映射亦有此性质,也可以将相空间分割成一系列的分叶线,并给每个分叶线赋予一个逆向的符号序列。 图2 M区中的部分正映射分叶线 对相空间重新分割以后,相空间中每个轨道点被赋予了一个双边无穷符号序列,所有相空间点的符号序列组成了一个符号空间。为了建立符号动力学,首先要对这些符号序列排序,规定大小、排序的基本原则是保持与相空间轨道点的拓扑关系一致。注意到正逆映射对于x分量的迭代只依赖于x坐标的值,不依赖于y的值(y坐标的值参与决定当前的轨道点属于哪一分区)。这一特性提示可以按照x值的大小给相空间上的分叶线排序,即固定y的值,要求x值大的点对应的分叶线的符号序列也大。据此,首先要求∙L<∙M<∙R。对于更长的符号字串,两个相邻的点(x1,y1)和(x2,y2),如果它们都属于L区或R区,正映射之后的像点保持原来的排序;如果这两个点属于M区,映射之后的像点与原来的排序相反。由此可知,对于两个符号序列,∙PL和∙PR,如果它们的公共字头P里含有偶数个M,那么其像点间的排序保持初始点间的排序,也就是说由∙L<∙R推出∙PL<∙PR。反过来,如果P含有奇数个M,由∙L<∙R推出∙PL>∙PR。按照这一原则,得到正序列的排序规则: 其中EM表示具有偶数个M的公共字头,OM表示具有奇数个M的公共字头。同样可以推出逆序列的排序规则: 其中EM表示具有偶数个M-1的公共字头,OM表示具有奇数个M-1的公共字头。按此规则,相空间中(-∞,1)和(∞,0)分别对应最小和最大的正向符号序列,(-∞,0)和(∞,1)分别对应最小和最大的逆向符号序列。 分叶线的排列规则对符号序列给出了基本的限定,只有当正映射分叶线∙Q和逆映射分叶线P∙相交,符号序列P∙Q才是允许的序列,对应相空间中真实的轨道点。如果正映射分叶线∙Q和逆映射分叶线P∙不相交,那么符号序列P∙Q不是允许的序列,由它生成的所有正向和逆向的移位序列也都是禁止的。 为了可视化讨论符号序列空间,通常为符号序列定义度规,从而在坐标平面上描述符号平面。为此我们定义∙s1s2…si…=∙Γi-1si…的“坐标”α为: 其中 同样定义…siˉ…s2ˉs1ˉ∙=…siˉΓi-1∙的“坐标”β为 其中 据此定义规定后,当前点的双边无限序列对应平面上单位正方形[0,1]×[0,1]内的一个点。例如R∞∙L∞对应(0,1)点,M∞R∙M∞对应(1/6,1/2)点。这个单位正方形称为符号平面,其上垂直线和水平线分别对应正、逆分叶线。 确定符号平面上的基本禁止区(BBZ)是建立符号动力学的关键步骤。基本禁止区定义为分割线在符号平面上的像,选定分割线M1(x=y)上的一点,设此点的符号序列是P∙m1Q,其中m1可以取M或R,则正映射分叶线∙m1Q被分解成两条,∙MQ和∙RQ,分别对应于所选定的点向左和向右无穷小扰动所对应的正映射分页线,那么所有介于∙MQ和∙RQ之间的正向分页线将不能和小于等于P∙的逆向分页线相交。对应到符号平面,这表示一个由一条β(P∙)和两条α(∙MQ)和α(∙RQ)围成的一个矩形区域,这个区域构成一个禁止区,由所有M1上的点生成一片禁止字区。同样由所有M2上的点可以生成另一片禁止字区,两片禁止字区构成了映射的基本禁止区。不过这样构造的禁止区讨论起了略显麻烦,可以进一步用更简单的方式给出等价的基本禁止区。注意到基本禁止区的定义是相对的,基本禁止区在正、逆映射下的任何一个像也都可以做为基本禁止区。换句话说,任何一条分割线的正、逆映射像也同样是分割线,可以等价地构造基本禁止区。在文章讨论的特殊系统中,可以简单算出M1一次正映射的像恰好是图1上边界(y=1)上的线段(-∞,b),M2一次正映射的像则恰好是图1下边界(y=0)上的线段(∞,b),这样可以利用这两条边界作为分割线构造基本禁止区:取(∞,b)上的一点,设此点的符号序列为P∙Q,则从分叶线的示意图和正、逆映射对称性可以发现,正映射分叶线具有正斜率,而逆映射分叶线具有负斜率,因此所有小于P∙的逆映射分叶线,都不可能和大于等于∙Q的正映射分叶线相交,从而在符号平面右下角定义了一个[αQ,1]×[0,βP]的矩形禁止区,所有(∞,b)上的点定义了符号平面右边的一片基本禁止区。同样地,所有(-∞,b)上的点定义了符号平面左边的一片基本禁止区。构造出基本禁止区后,允字条件表述为:在任意移位操作下都不落入基本禁止区的符号序列是允许的。 图3 台球映射的符号平面 图3给出了参数b=π/5时的符号平面及基本禁止区,同时还给出了一条60000个点的真实轨道对应的符号序列在符号平面上的轨迹,可以看到这些点都落在基本禁止区外部。一个明显的特征是这些轨迹大部分基本重合在一起,表明该参数下台球映射只有数量非常少的允许符号序列或允许运动轨道,这远少于一般的二维映射如Henon映射情况下符号平面上的允许轨道,这一现象是此系统不具有遍历性的一个证据。 符号动力学分析方法的一个重要的优点是可以进行定性分析。下面举一个简单的例子,以符号动力学分析判断系统在参数b=0下的可能允许或一定禁止的周期轨道。通过计算,可以得出此参数下符号空间最小和最大的正向符号序列,也就是相空间中(-∞,1)和(∞,0)分别对应的正向符号序列,分别为∙LM∞和∙RM∞,所以一个允许的符号序列∙Q必须满足 显然LL和RR的字符串都不满足此条件,因此周期一轨道L∞和R∞都不是允许的轨道,而M∞满足以上限制条件,因此是一条可能的周期轨道。对于周期二的轨道,由于∙(ML)∞<∙LM∞而∙(RL)∞>∙RM∞,所以这两个周期轨道都被禁止。这样只有(RL)∞满足限制条件,是可能存在的周期轨道。同样的方法用于周期三轨道,发现只有(MRL)∞和(MLR)∞是可能存在的周期轨道,继续分析更高周期的轨道。可以发现只有形如(M(RL)k)∞的周期轨道是可能存在的。可能存在的轨道是否实际存在还需要进一步利用允字条件针对完整的基本禁止区分析确定,不过这些初步结果已经可以帮助我们理解该系统的一些动力学行为,例如(M(RL)k)∞表明系统存在一系列的回溯运动,它可以任意多次地重复(RL)的二周期运动,这是在数值模拟过程中最普遍的一种运动,是系统非遍历性的关键机制。 文章成功构建了直角三角形台球映射的符号动力学描述,建立了符号序列和相空间中正、逆向映射的分叶线的对应,并推导出其各自的排序规则。为了对符号空间的运动给出直观描述,引入了符号序列的度规表示,把符号序列空间映射成为符号平面,并建立了符号平面上的基本禁止区。利用这一符号动力学框架,可以分析禁止符号序列和可能允许的符号序列,从而定性理解系统的动力学行为。 [1]G.Casatiand T.Prosen,Phys[J].Rev.Lett,1999(83):4729. [2]Roberto Artuso,Giulio Casati,and Italo Guarneri.Numerical study on ergodic properties of triangular billiards[J].Physical Review E,1997,55(6):6384. [3]JunxiangHuangand Hong Zhao.Broken ergodicity of right triangular billiard systems[J].arXiv:2016,1603.06209. [4]Eugene Gutkin.Billiards in polygons:survey of recent results[J].Journalofstatisticalphysics,1996,83(1):7-26. [5]EugeneGutkin.Billiard dynamics:An updated surveywith theemphasison open problems[J].Chaos,2012,22(2):6116. [6]GGalperin and D Zvonkine.Periodic billiard trajectories in right trianglesand right-angled tetrahedra[J].Regularand Chaotic Dynamics,2003,8(1):29-44. [7]Serge Troubetzkoy.Periodic billiard orbits in right triangles[J].In Annalesde l’institut Fourier,2005,(55):29-46. [8]W Patrick Hooper.Periodic billiard paths in right trianglesareunstable[J].Geometriae Dedicata,2007,125(1):39-46. [9]Bai-Lin HaoandWei-Mou Zheng.Applied symbolic dynamicsand chaos[J].World scientific,1998,(7). Symbolic Dynamic Analysis of Right Triangular Billiard HUANG Jun-xiang1,Lu Jun-zhe2,ZHAO Hong1 The symbolic dynamics or the right triangular billiard is studied in this paper.A two-dimensional piecewisemap is constructed to describe the billiard dynamics.Themap has two partition lines which appear as straight lines.The phase space is thus foliated flowing the forward and backwardmaps in a simplemanner.With the help of thebasic forbidden zoneon the symbolic plane,the dynamicsof the system isstudied primarily. Triangular Billiard;Symbolic dynamics;Ergodicity O192 A 1008-9659(2016)02-0051-05 2016-02-25 国家自然科学基金项目(11335006);新疆师范大学本科教学质量工程建设教学研究与改革项目(SDJG2016-10)。 黄俊翔(1990-),男,福建漳州人,硕士研究生,主要从事非线性动力学研究。 *[通讯作者] 赵 鸿(1964-),男,甘肃永昌人,教授,主要从事非平衡统计物理研究。
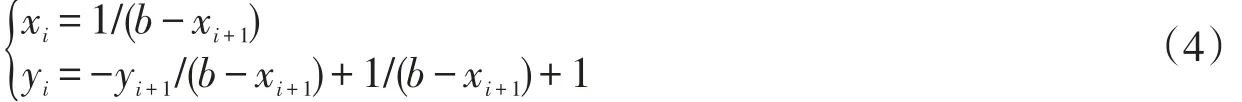


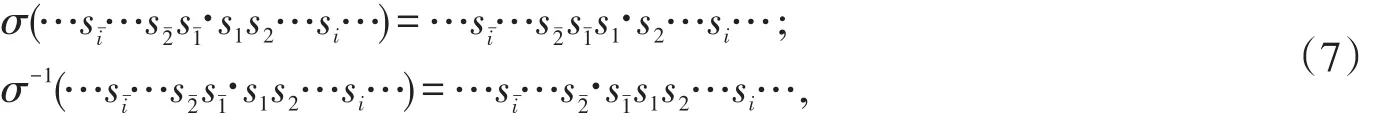
2 相空间的分叶线的符号序列以及排序规则



3 符号平面和允字条件






4 总结
(1.DepartmentofPhysics,Xiamen University,Xiamen,Fujian,361005,China;2.College ofPhysicsand Electronic Engineering,Xinjiang Normal University,Urumqi,Xinjiang,830054,China)
