超大滑滚比下角接触球轴承热弹性流体动力润滑分析
2016-07-25张彬彬王静
张彬彬,王静
(青岛理工大学 机械工程学院,山东 青岛 266033)
大滑滚比是两物体表面反向运动,在这种特殊的工况下,弹流润滑的典型特征即中央平坦区和出口颈缩消失。内燃机凸轮-挺杆机构[1]、无保持架的滚动轴承[2-3]、直线导轨等工作在大滑滚比甚至零卷吸工况下,该工况下,润滑剂的双向流动造成了其数值求解困难。文献[4-5]首次给出了超大滑滚比下的线接触热弹流数值解。文献[6]研究了表面速度对点接触零卷吸凹陷深度的影响。文献[7]研究了流体的流变性对线接触零卷吸热弹流的影响,发现使用Ree-Eyring流体表面速度的降低使椭圆形中心凹陷减小并且在极低速下接触区的油膜非常薄,接近Hertz干接触。下文研究了超大滑滚比下,滑滚比对无保持架角接触球轴承热弹性流体动力润滑的影响。
1 控制方程
采用润滑理论中最常用的非牛顿Ree-Eyring流体模型,其本构方程为[8]
(1)
式中:u为流体速度;τ0为特征剪应力;η为流体的表观黏度;τ为流体剪应力。
将无保持架角接触球轴承中两相邻钢球的接触等效为图1所示的大滑滚比问题,定义下弹性固体为a,上弹性固体为b,表面速度分别为ua,ub,二者方向相反,故滑滚比S=2.0(ua-ub)/(ua+ub)>2.0。定义固体a的速度方向为x轴,垂直于卷吸速度方向为y轴,油膜厚度方向为z轴。

图1 点接触大滑滚比模型
时变点接触广义Reynolds方程为[9]
(2)

(2)式的边界条件为
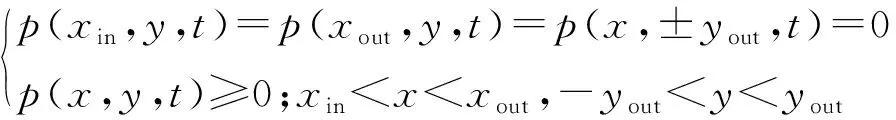
,(3)
式中:下标“in”和“out”分别为压力计算域的入口和出口边界。
点接触几何方程,即膜厚方程为[8]

(4)
式中:h00(t)为刚体位移;Rx,Ry分别为两固体在x,y方向的综合曲率半径;E′为两固体的综合弹性模量。
载荷方程为

(5)
Roelands黏压-黏温关系式为[8]
η=η0exp{A1[-1+(1+A2p)Z0(A3T-A4)-S0]}
,(6)
A1=lnη0+9.67,A2=5.1×10-9,
式中:η0为润滑油的环境黏度;T0为环境温度,T为油膜温度;Z0,S0分别为黏压、黏温系数,与润滑油的黏压系数α和黏温系数β的关系为
(7)
密压-密温关系式为[8]
, (8)
式中:ρ0为润滑油的环境密度。
由于在x,y方向上的热传导与z方向相比要小的多,故可以忽略不计[10]。忽略热辐射,油膜能量方程可写为[8]
(9)
式中:c为润滑油的比热容;u,v分别为润滑油在x,y方向的流速;κ为润滑油的热导率。
(9)式的边界条件为
(10)
两固体的能量方程为[8]
(11)
式中:ca,cb分别为固体a,b的比热容;ρa,ρb分别为固体a,b的密度;κa,κb分别为固体a,b的热导率。
沿z方向,两固体的温度边界条件为
(12)
式中:za,zb分别为固体a,b内与z同向的坐标;d为固体内变温层的深度。
沿运动方向,固体a,b的温度边界条件为
(13)
在固-液界面的热流量连续条件为[8]
(14)
固体a的速度保持恒定,固体b的速度反向增大至所需速度,形成大滑滚比工况,固体b的速度为
(15)
t0=2π/ω,t2=5t1/4,
式中:ω为固体a的角速度;t1分别取0.08t0,0.16t0,0.26t0和0.5t0,相应的滑滚比分别为3.3,6.0,14.0和∞。
2 数值方法
为了便于分析求解,改善计算过程的数值稳定性,需对上述方程进行量纲一化,定义如下
式中:a′为Hertz接触区半宽;pH为最大Hertz接触应力;u0为速度的参考量,其取值对结果没有影响。
上述公式由压力-温度的反复迭代求解。在压力求解过程中,温度场当作已知变量。Reynolds方程、膜厚方程由多重网格方法求解,其中弹性变形使用多重网格积分法[11]计算,编写Fortran程序进行求解。压力求解使用4层网格,最高层网格在x,y方向的节点数分别为513和197,在y方向使用半域求解。在温度求解过程中,压力场当作已知变量,温度场求解采用逐列扫描技术[12]。因为xin和xout既是上游边界又是下游边界,所以对温度场的逐列扫描必须是双向的。在油膜内z方向有11个等距节点,固体a和固体b内沿za-和zb-方向分别有6个非等距节点。温度场每层网格上节点数与压力求解中最高层网格节点数一致。结果分析中使用量纲一化膜厚H=(h/Rx)×105,在最顶层网格上的收敛判据为
(15)
3 结果与分析
70000V型无保持架角接触球轴承材料(GCr15)和润滑油参数见表1。轴承主要用于航空器[2,13],可承受较大的载荷,回转速度高、低均可,噪声低,振动小,摩擦扭矩低。由于拆除了保持架,其与传统轴承相比,可多放2个钢球,该类型轴承的主要失效形式为润滑不良及大滑滚比下油膜的失效。文中载荷为W=31.618 N(pH=0.5 GPa)。

表1 轴承材料和润滑油参数
3.1 超大滑滚比对压力、膜厚的影响
大滑滚比下压力和膜厚的分布曲线如图2所示。当滑滚比S=3.3时,压力曲线中只存在一个压力峰,在压力峰对应位置处有一个小的油膜凹陷。在大滑滚比的工况下,固体a由于尚未进入接触区,其表面温度低,故可从接触区左侧携带高黏度的润滑油进入接触区;固体b由于刚离开接触区,其表面温度高,故可从接触区带走低黏度的润滑油。在膜厚方向上黏度高的润滑油速度梯度较小,而黏度低的润滑油速度梯度较大,从而使进入接触区的润滑油有多于离开接触区润滑油的趋势,为了维持质量守恒,接触区内必然产生压力梯度以增大接触区润滑油的黏度,且这种趋势随着滑滚比的增大逐渐增强。随着滑滚比的增大,压力峰值增大,油膜凹陷变深并且其位置朝入口区方向移动。当S达到∞时,即零卷吸工况,压力峰和油膜凹陷在接触区中心,压力主峰两侧出现2个小的压力峰,对应位置处的膜厚变得低垂。

图2 不同滑滚比下Y=0截面压力、膜厚分布
大滑滚比下膜厚等值线图如图3所示。当S=3.3时,膜厚等值线图呈现马蹄形,在出口区存在椭圆形的油膜。随着滑滚比的增加,马蹄形逐渐削弱,椭圆形油膜变为椭圆形的凹陷且面积扩大。当S=14.0时,马蹄形消失,随着S的继续扩大,椭圆形凹陷移至接触区中心,两侧出现2个细长月牙。

图3 不同滑滚比下膜厚等值线图
3.2 超大滑滚比对油膜温升的影响
大滑滚比下Y=0截面油膜温度场分布如图4所示。当滑滚比S=3.3时,油膜温升较大;当滑滚比S=6.0时,由于固体b携带进入接触区的润滑油增多,故温升降低,温度场出口区有一个小的波动;当S=14.0时,出口区出现一个小的温度峰;在零卷吸工况下(S=∞),温度峰值变大且位于接触区中心,温度场主峰两侧2个小压力峰的位置发生微小的波动。随着S的增大,温度场呈先减小后增大的趋势,固体a表面出口区由于固体b携带进入接触区的润滑油逐渐增多,故温升逐渐降低。

图4 不同滑滚比下Y=0截面油膜温度场三维分布
3.3 超大滑滚比对润滑油流速的影响
大滑滚比下Y=0截面油膜流场分布如图5所示。当S=3.3时,对应于压力峰的位置在出口区产生一个大的流场波动,随着滑滚比的增加,流场的波动呈先减弱后增强的趋势;当S=14.0时,流场沿z方向在出口区呈反“S”形分布;随着滑滚比的继续增大,该形状更加明显且移至接触区中心,使靠近两固体表面的润滑油层流速变化减小,几乎不流动,该现象是零卷吸这一特定工况下的产物,由特定的温度和卷吸速度决定[14]。
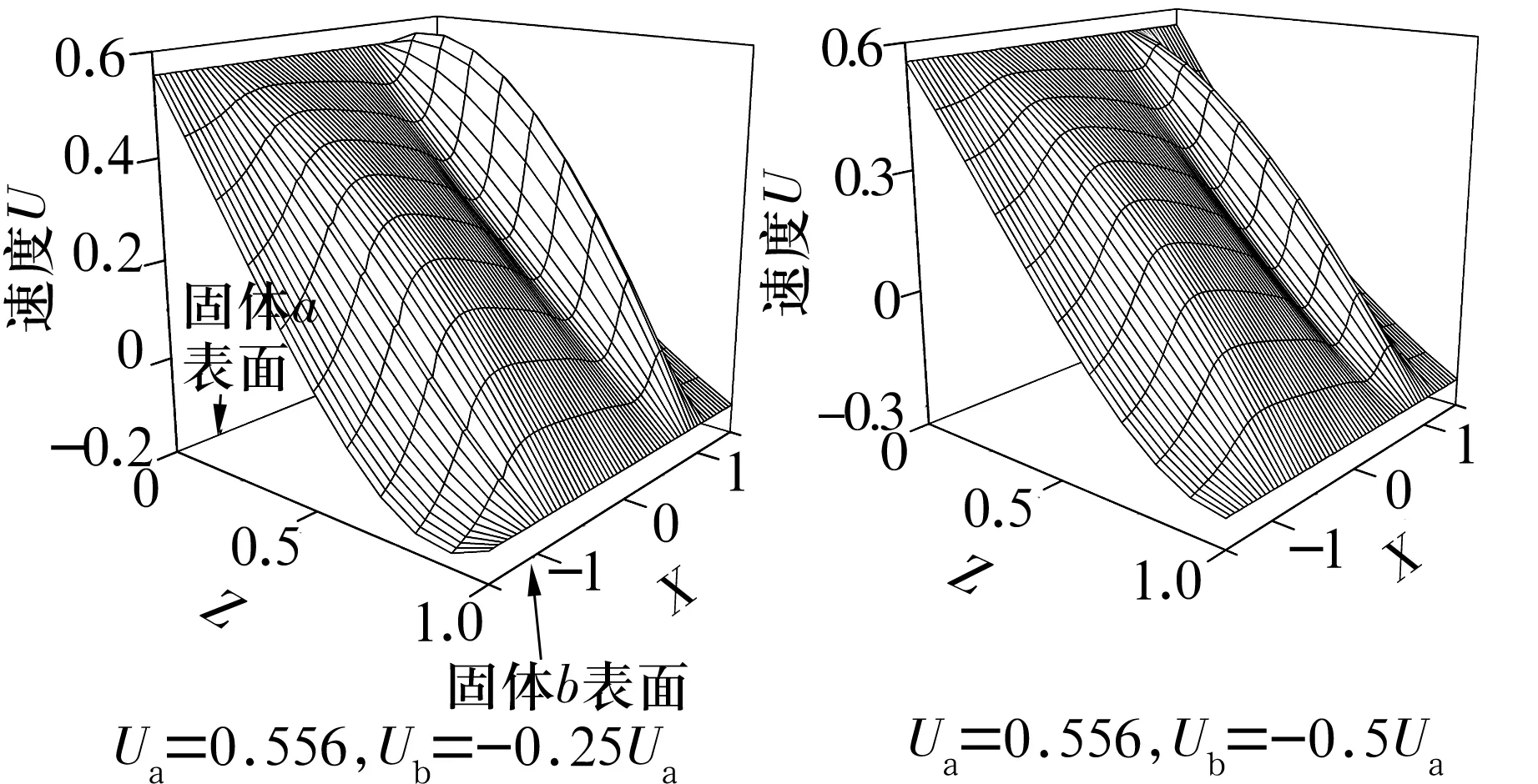
(a)S=3.3 (b)S=6.0
3.4 超大滑滚比对油膜剪应力的影响
大滑滚比下Y=0截面油膜剪应力分布如图6所示。当S=3.3时,存在一个剪应力峰值,随着滑滚比的增大;当S=6.0时,油膜的剪应力明显增大且产生2个剪应力峰;随着S的扩大,油膜的剪应力继续增长直至产生2个小的剪应力峰和一个主峰,两固体表面的速度差逐渐变大,故油膜剪应力不断变大。
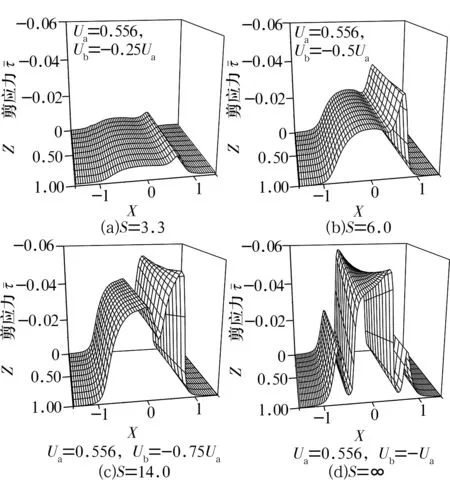
图6 不同滑滚比下Y=0截面油膜剪应力三维分布
3.5 小结
综上所述,随着滑滚比的增加,油膜压力峰、温升和剪应力均呈现增大的趋势,油膜压力的增大会导致两固体弹性变形增大,温升和剪应力的增大对润滑油不利,故滑滚比越小越好。
4 结论
1)随着滑滚比的增大,出口区油膜凹陷朝入口区方向移动,压力峰变大,中心凹陷加深。当达到零卷吸工况时,接触中心压力最大,压力主峰两侧产生2个小压力峰。
2)随着滑滚比的增加,油膜温度场呈先变大后减小的趋势。零卷吸工况下,接触区中心产生一个大的温度峰,两侧有小波动。
3)随着滑滚比的增加,流场的波动朝入口区方向移动。在零卷吸工况下,接触区中心处油膜的流场呈反“S”形,靠近两固体表面的润滑油几乎不流动。
4)随着滑滚比的增加,油膜剪应力不断变大。在零卷吸工况下,油膜剪应力出现1个主峰和2个侧峰。
