GCr15轴承钢可靠性模型的探讨

夏新涛，白阳，孙立明，叶亮，朱文换

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.洛阳轴研科技股份有限公司，河南 洛阳 471039；3.河南省高性能轴承技术重点实验室，河南 洛阳 471039；4.滚动轴承产业技术创新战略联盟，河南 洛阳 471039)

GCr15钢是一种合金含量较少、性能良好、应用最广泛的高碳铬轴承钢。经过淬火加低温回火后具有较高的硬度、均匀的组织、良好的耐磨性和接触疲劳性能。在以往对GCr15轴承钢的研究中，已经从材料成分、表面加工、淬火处理等方面对其性能进行了研究，旨在从不同的方面提高材料的性能[1-2]。

下文对GCr15轴承钢可靠性模型进行研究，通过试验得到其失效数据，分别用Weibull分布[3-4]和对数正态分布[5-7]进行参数估计，得出2种分布与经验函数的标准差，并通过比较2种分布的标准差，得出拟合度较高的可靠性模型。根据试验数据，不同批次的GCr15轴承钢，需要具体分析、选择合适的可靠性模型。

1 可靠性模型

对数正态分布的概率密度函数为

(1)

分布函数为

(2)

可靠度函数为

R(t)=1-F(t)=

(3)

式中：t为寿命的随机变量，t>0；μ为比例参数；σ为形状参数，σ>0。

Weibull分布的概率密度函数为

(4)

分布函数为

(5)

可靠度函数为

(6)

式中：η为比例参数，η>0；β为形状参数，β>0。

2 可靠性模型评估方法的验证

用计算机生成一组对数正态分布的随机数，令对数正态分布参数(μ,σ)=(4，0.4)，个数n=30，t1=[29.09,30.22,32.78,34.66,38.35,45.32,48.84,51.61,56.07,63.90,65.64,67.08,69.18,72.84,74.99,75.45,77.45,82.25,82.55,84.01,95.65,103.22,103.85,111.42,124.51,132.89,133.01,137.55,167.45,225.53]。

使用极大似然法[8]对t1进行参数估计,可得μ=4.389 6,σ=0.467 0，将其代入(3)式得到相应的可靠度函数。

相应的经验分布函数通过Nelson方法[3-4]得到，也可称为近似中位秩公式，即

(7)

式中：i为失效试件的顺序号；ti为第i个失效试件的试验时间。

根据上述结果绘出可靠度函数曲线，如图1所示，并将t1代入(7)式得到经验点。由图可以看出，可靠度曲线基本符合经验点的分布。用K-S检验方法[8]，显著性水平α=0.05，得到对数正态分布拟合模型的K-S检验值为0.08，其临界值Dc=0.241 7，假设成立概率P=0.99，检验值小于临界值，且假设成立概率高，证明以极大似然法对对数正态分布进行参数估计的效果较好。

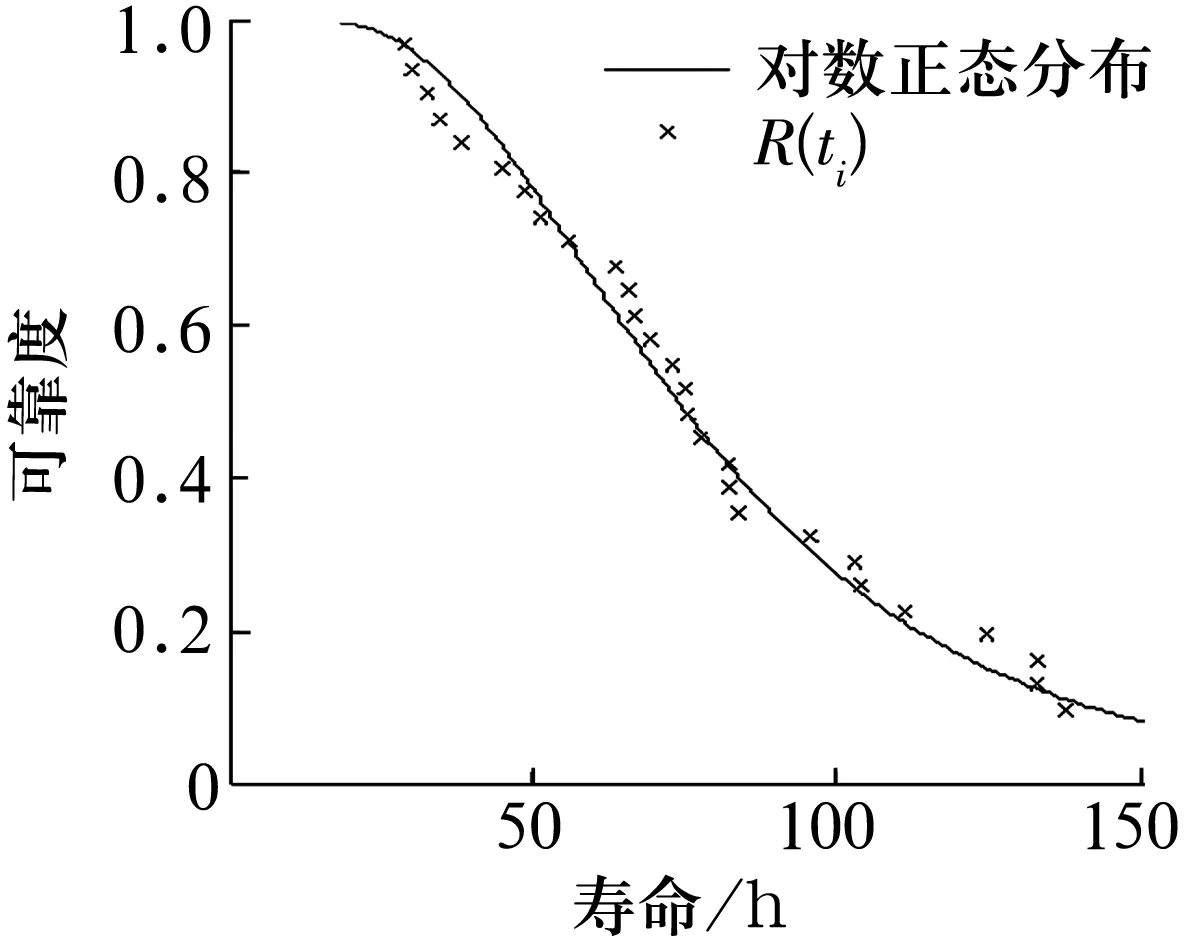
图1 对数正态分布随机数可靠度函数曲线

利用计算机生成一组Weibull分布的随机数，令对数正态分布参数(β,η)=(2.5，60)，个数n=30，t2=[10.20，15.76,17.91,22.11,28.86,32.11,36.24,37.83,39.54,40.82,43.79,46.44,47.32,47.40,48.79,50.85,55.76,59.56,59.64,61.19,61.42,64.26,67.89,69.02,71.94,76.63,76.76,77.27,85.23,114.40]。

使用极大似然法对t2进行参数估计,可得β=2.474 4,η=58.829 0。

利用该结果绘出可靠度函数曲线，如图2所示，将t2代入(7)式得到经验点。由图可以看出，可靠度曲线基本符合经验点的分布。用K-S检验方法，显著性水平α=0.05，得到极大似然法估计的Weibull分布拟合模型的K-S检验值为0.077，其临界值Dc=0.241 7，假设成立概率P=0.99，检验值小于临界值，且假设成立概率高，证明以极大似然法对Weibull分布进行参数估计的效果较好。

图2 Weibull分布随机数可靠度函数曲线

3 试验案例的可靠性分析

在以往的轴承钢寿命试验中，因Weibull分布拟合性良好，大多都将其作为轴承钢寿命的可靠性模型。但通过试验计算表明，不同批次的GCr15轴承钢，Weibull分布和对数正态分布作为可靠性模型的拟合性各有优劣，通过以下2个案例进行说明。

试验所使用的轴承钢失效数据由NTN寿命试验机试验所得。将不同厂家2个批次的GCr15钢，在相同的热处理条件下制作成直径12 mm，长22 mm的圆柱滚子试样，并将其装入寿命试验机中由导辊带动，转速为4 080 r/min，对滚子施加2.55 kN的径向载荷。从开始试验时计时，直到试样表面剥落失效，试验结束，每个试件的试验时间即为要收集的失效数据。

3.1 案例一

失效数据个数n=26，T1=[0.38,1.69,1.69,1.71,1.80，1.86,1.89,2.06,2.14,2.20,2.42,2.46,3.88,4.89,6.20，7.73,12.46,12.50，12.88,13.33,31.97,38.57,47.50，50.20,51.77,58.71]。将T1代入对数正态分布模型进行参数估计可得μ=1.786 1,σ=1.371 1；将T1代入Weibull分布模型进行参数估计可得β=0.759 0,η=12.023 6，失效数据的可靠度函数曲线如图3所示。

图3 T1组失效数据可靠度函数曲线

由图3可以看出，2种可靠度曲线基本符合经验点的分布，二者均表现出良好的拟合度。计算可靠度函数与经验点的标准差，用K-S检验方法，显著性水平α=0.05，对参数估计结果进行假设检验。寿命失效概率为90%和50%时的寿命值t是研究可靠性的重要指标。令可靠度函数R(t)=0.9时，t=P1；R(t)=0.5时，t=P2。T1组失效数据2种可靠性模型的对比结果见表1。

表1 T1组失效数据2种可靠性模型的对比结果

由表1可知，2种模型的K-S检验值均小于临界值，其均为符合该组失效数据的恰当模型。其中对数正态分布相对于经验点的标准差小于Weibull分布，因此，在2种分布均满足该组失效数据的前提下，对数正态分布的拟合度要更高，将其作为可靠性模型更合适。以标准差小的对数正态分布为基准，分别计算2种分布在失效概率为90%和50%时寿命的相对误差f1和f2为

虽然2种分布的标准差相距甚微，仅为1%，但在相同的失效概率前提下，以标准差小的分布为基准，其寿命的相对误差非常大。因此，为减小寿命估计误差，在该案例中应选择标准差小的对数正态分布做为可靠性模型。

3.2 案例二

失效数据个数n=30，T2=[0.61,0.69,1.66,1.81,1.91,1.93,2.34,2.36,2.38,3.07,3.07,3.08,3.63,11.80,12.67,14.18,14.29,16.27,17.84,18.83,26.10,28.00,29.79,47.52,47.86,52.91,53.15,53.57,80.20,90.11]。将T2代入对数正态分布模型进行参数估计可得μ=2.208 1,σ=1.467 5；将T2代入Weibull分布模型进行参数估计可得β=0.786 3,η=18.696 1，失效数据的可靠度函数曲线如图4所示。

图4 T2组失效数据可靠度函数曲线

由图4可以看出，2种可靠度曲线基本符合经验点的分布，二者均表现出良好的拟合度。计算可靠度函数与经验点的标准差。用K-S检验方法，显著性水平α=0.05，对参数估计结果进行假设检验。T2组失效数据2种可靠性模型的对比结果见表2。

表2 T2组失效数据2种可靠性模型的对比结果

由表2可知，2种模型的K-S检验值均小于临界值，均为符合该组失效数据的恰当模型。其中Weibull分布相对于经验点的标准差小于对数正态分布。以标准差小的Weibull分布为基准，失效概率为90%时的相对误差f1=30%；失效概率为50%时的相对误差f2=29%。因此，对于该批次的GCr15轴承钢，Weibull分布的拟合度优于对数正态分布，选择Weibull分布作为可靠性模型更合适。

4 结束语

对采用对数正态分布和Weibull分布作为失效数据可靠性模型进行假设检验，结果证明，2种可靠性模型均可满足失效数据。对于不同批次的GCr15轴承钢，在实际计算中，应选择标准差小的分布作为可靠性模型，从而减小寿命估计误差，提高计算精度。