差分振子在滚动轴承故障诊断中的应用

刘燕，胡学青,刘浩，张明玉

(宿州学院 煤矿机械与电子工程研究中心，安徽 宿州 234002)

滚动轴承发生故障时，其振动信号往往呈现出强烈的非平稳性及非线性特征，轴承早期故障信号的特征相对微弱，容易淹没在其他振动信号和随机噪声中，采用传统的时频分析方法[1-3]很难从混有强背景噪声的振动信号中提取微弱故障信息。混沌振子法[4-6]和随机共振法[7-9]已经广泛应用于微弱信号的检测中。差分振子法[10]的运算代码为加减运算，速度快，更适合对运算速度要求较高的场合；而且不受检测信号相位的影响，检测结果更加准确。另外，差分振子有一定的容错特性，可在一定程度上消除加工误差导致的计算频率偏差；而且不用过滤噪声，噪声只会使相图周围变得粗糙，并不影响整个系统的稳定性。

目前，关于差分振子的研究较少，文献[11]将差分振子方法应用于同步发电机转子匝间短路及转子碰摩故障的识别中，取得了良好的效果；文献[12]将差分振子方法轴承故障和齿轮故障的早期数据进行了分析，成功地提取出了故障早期的微弱特征。在此，将差分振子方法应用于滚动轴承故障诊断中，基于其检测带宽特性和幅值检测特性实现轴承的早期故障检测。

1 差分振子检测器的构造

差分振子检测器是以二元差分方程为基础构造的检测器[11]，具体数学模型如下

(1)

令α=-(a+d)，β=ad-bc，f(k)=bp·

cos(2kπfe+2kπfd/fs) ，则(1)式可简化为

xk+2+αxk+1+βxk=f(k)T(k) ,

(2)

式中：a,b,c,d为差分振子的系统参数；p为放大倍数(一般取整数，1，2，4，8)；fe为系统激励频率；fd为待检测频率；fs为输入信号的采样频率；T(k)为输入信号。

2 差分振子参数设置原则

差分振子设置原则如图1所示：首先，确定差分振子系统参数，通过仿真确定最合适的系统参数；其次，确定系统激励频率fe，用差分振子检测信号，必须使系统激励频率等于系统固有频率，即f0=fe(f0=ω0/2π ，ω0=arccos[-α(1+β)/4β] )，否则不能检测信号；然后，确定检测频率fd，若被测信号中含有fd这一频率成分, 则系统产生共振, 噪声得到抑制，不需要滤噪，其相图随即发生变化;最后，通过观察系统的相图变化判断系统是否含有待检测频率，从而可以实现早期故障的检测。

当向差分振子系统中输入待检测信号后，若差分振子相图收敛于极环，则信号中含有待检测频率信号；反之，如果收敛于极点，则可能检测信号中本来就不存在待检测频率信号，或者是待检信号中噪声信号强度过大，导致信噪比过低，无法检测出待检测频率信号。

3 差分振子特性

3.1 检测带宽特性

构造仿真函数

T(k)=0.1sin(2kπ×17)+g·randn(k) 。

(3)

在检测过程中，将检测频率设置成以17 Hz为中心的一系列取值，对输入信号中的17 Hz的频率成分进行检测。差分振子参数设置为：α=0.97；β=0.97；fe=0.331 9 Hz；x0=8；y0=8;fs=1 000,p=1,g=0.1(随机噪声方差)。从图2可以看出，当检测频率为18 Hz时，相图也收敛于极环，说明待检测信号中含有17 Hz的频率成分，此时最大检测带宽为1 Hz，在工程应用中是允许的。

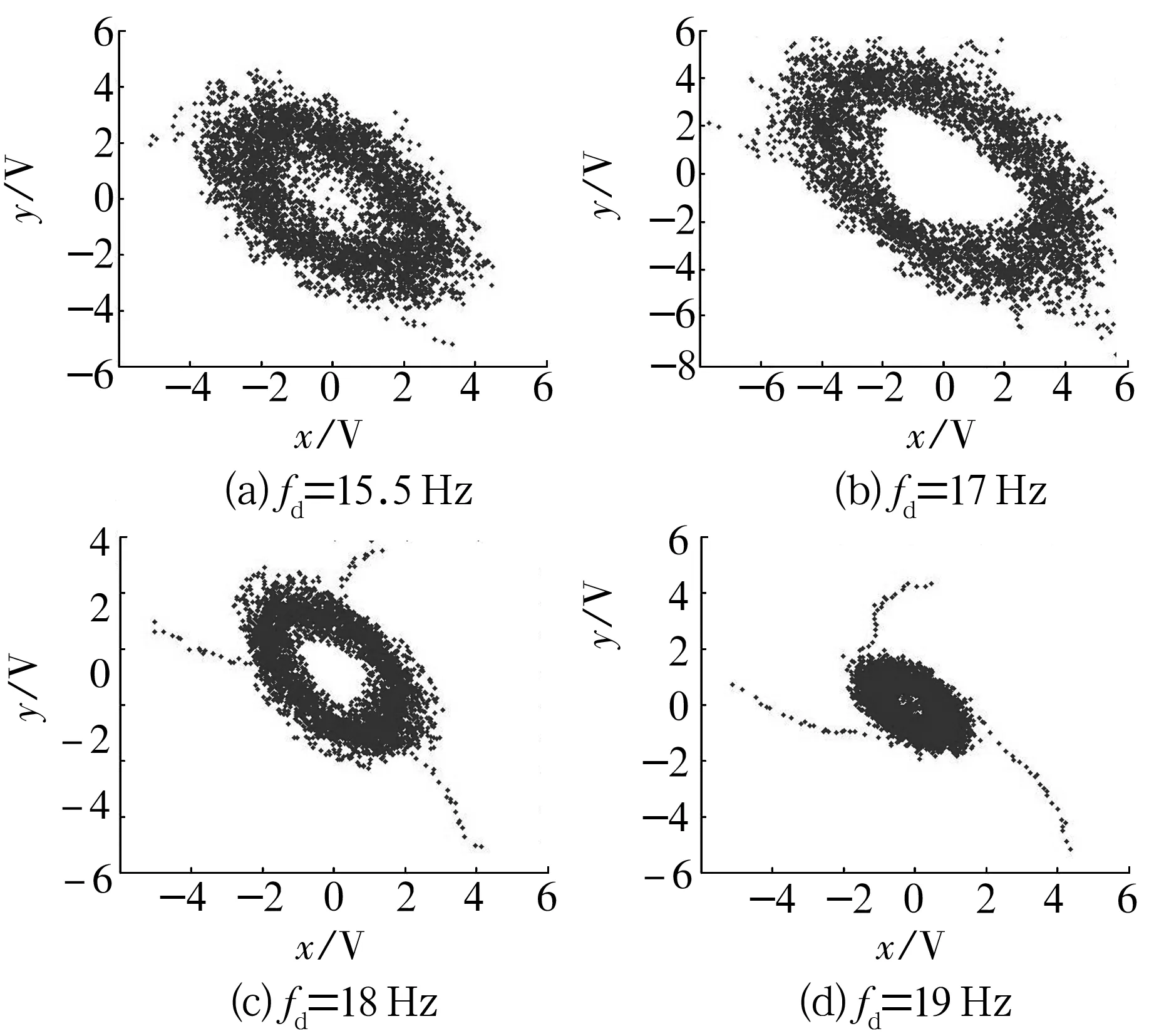
图2 不同检测频率下的差分振子相图

仿真表明：差分振子的检测频率有一个波动范围，以检测频率为中心，以B=2b/fs为带宽的频率均敏感，即差分振子检测有一定的检测带宽。带宽的大小与α和β的取值有很大的关系，其中β的取值越大，差分振子的容错性能越差，检测带宽越宽。在工程实际中，由于考虑到各种误差的存在，一般不将α和β值取得很大，通常更加注重差分振子的容错性能。

3.2 幅值检测特性

在工程实际中，信号频率的提取很重要，而信号幅值的检测依然是一个难题。

设待检测信号为

s(t)=Acos(2πt×50)+0.2randn(1,t) ，

(4)

式中：A为信号幅值。

差分振子参数设置为：a=0.03,b=1.0,c=-1,d=-1,x1=5,y1=5,fe=0.331 9,fd=50,fs=1 000,p=1。则不同信号幅值下的差分振子相图如图3所示。

从图3可以看出，噪声强度相同时，相图的大小与幅值有着很紧密的关系，幅值越大，相图越大，相图的变化与幅值的增加呈线性比例关系。为了证明此结论，给定输入信号D(k)，设对应差分方程的解为ck，代入差分方程得

ck+2+αck+1+βck=f(k)D(k) 。

(5)

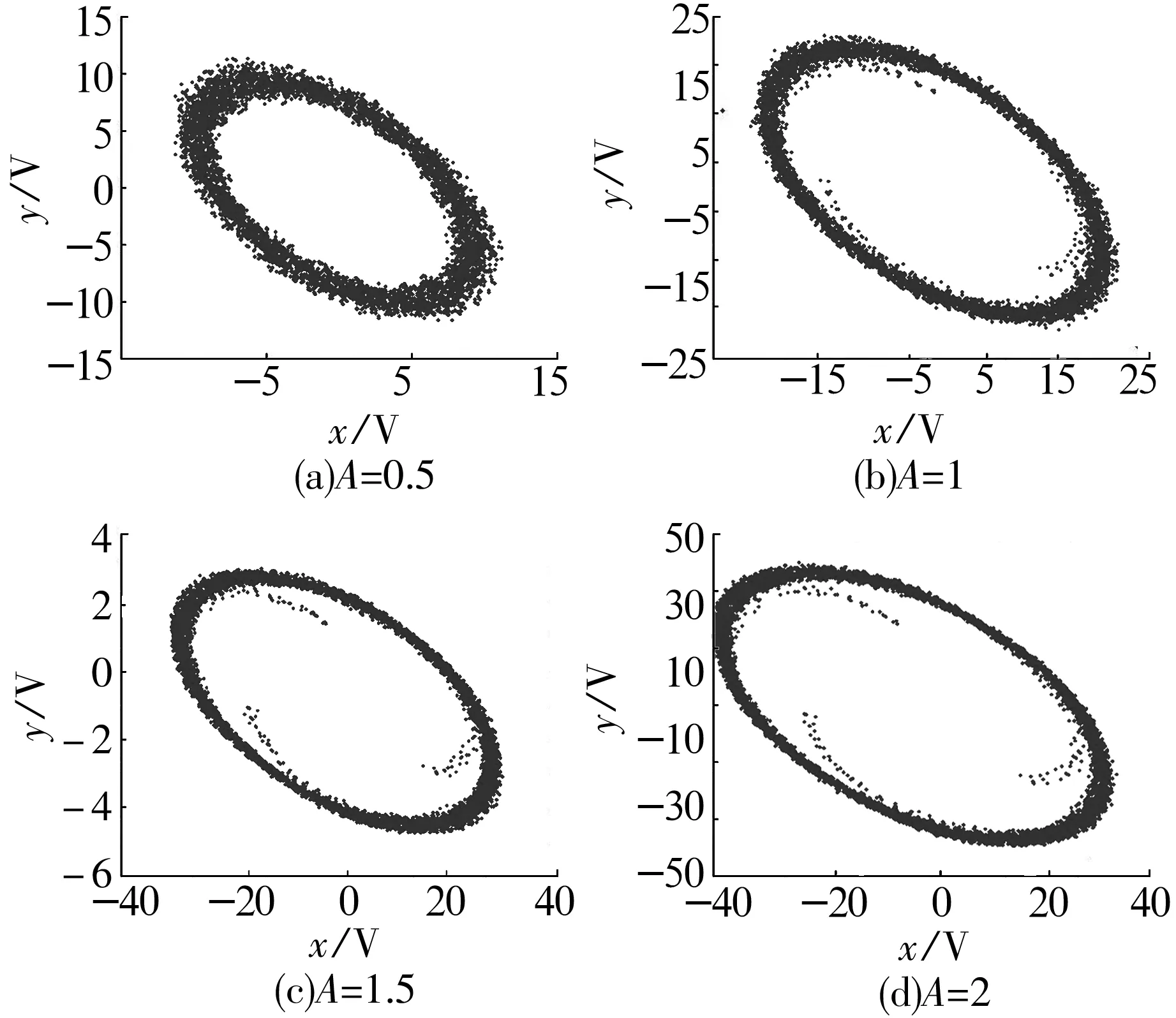
图3 不同信号幅值下的差分振子相图

如果输入信号的幅值增大到原来的k倍，即S(k)=kD(k)。假设S(k)对应方程的解为yk，则

yk+2+αyk+1+βyk=f(k)S(k)。

(6)

将(5)式两边同乘以k得

kck+2+α(kck+1)+β(kck)=kf(k)D(k)。

(7)

对比(6)式和(7)式可知

yk+2=kck+2，

(8)

可见输入信号的幅值增大k倍，差分振子方程的解也增大了k倍，则相应的差分振子相图也扩大了k倍。所以呈单调递增的线性关系。此结论为可视化检测故障提供一定的依据。

4 工程应用实例

试验轴承型号为30210型圆锥滚子轴承，采用SG双色金属刻字机模拟滚子早期点蚀故障，故障直径约0.3和0.5 mm，深度约几十微米。选用BVT-5轴承振动测量仪，径向与轴向加载力分别为150和120 N，采样频率为5 120 Hz，主轴转速为1 800 r/min。根据轴承参数计算得滚子故障特征频率为103.16 Hz。使用加速度采集仪采集故障信号并导入MATLAB，其时域波形如图4所示，经FFT处理后得到的频谱图如图5所示。

从图4中完全看不出故障特征频率，而在图5中也无法精确找到对应的滚子故障特征频率，特征频率完全被噪声所淹没。因此，依靠传统的时频方法无法准确判断轴承故障。

图4 信号的时域波形

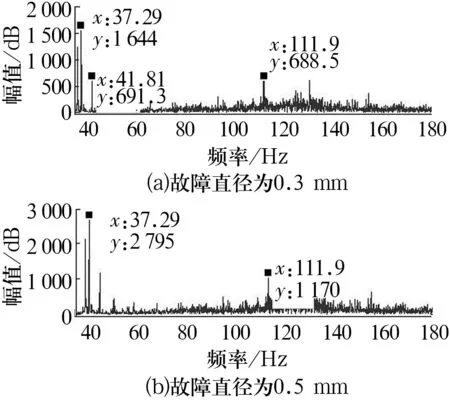
图5 信号的幅值谱

令α=0.97，β=0.999，fe=0.330 6 Hz，p=2。当fd=103.16 Hz时，得到的差分振子相图如图6所示。从图中可以看出，故障直径为0.3 mm的差分振子相图收敛的极环面积明显小于故障直径为0.5 mm的差分振子相图，随着故障直径的增大，滚子损伤的区域越来越大，故障有恶化的趋势。说明差分振子不但可以检测信号的频域信息，也可以直观观察信号的幅值信息。

图6 信号的差分振子相图

5 结束语

差分振子法可通过连续观察相图大小的变化，从而发现故障信号幅值的变化，在线观察故障变化趋势。但检测微弱信号时涉及参数很多，且每个参数的取值均由仿真得来，尚无理论推导，目前关于差分振子的研究工作还处于初期阶段，有待进一步研究。