小学数学课堂教学方法的研究

□胡仁军



小学数学课堂教学方法的研究

□胡仁军

【摘要】“几何几何，想破脑壳。”这句话是对小学几何知识难度之大的精辟概括。小学几何又分平面几何、立体几何，立体几何是小学几何的难点，主要体现在两个方面：让学生在大脑中构建几何模型、培养空间立体感是一难，培养学生的空间思维、解决生活中的实际问题是二难。如何让学生突破立体几何的难点，不怕立体几何、爱上几何，是值得小学数学教师思考的问题。解决这一问题，通过画图分析是一种行之有效的好方法。

【关键词】几何；画图；容易

一、画图，建构模型

在实际教学中常常会出现这样的现象：教师经常拿着长方体、正方体、圆柱、圆锥等实物模型授课，学生对这几种几何图形的特征也能说出一二。一旦实物模型拿走了，学生对各种立体图形的特征就渐渐模糊，立体感、空间感的建构更无从下手。即使死记硬背各种立体图形的特征，也往往是今天记住，明天忘记。如何打破这种僵局，让学生在脑海中建构模型、产生空间感？笔者通过教学实践和研究，发现画图能起到立竿见影的效果。

例如，教学长方体、正方体、圆柱体、圆锥体等立体图形时，让学生画一画这4种图形的特征，这样就能牢记心中，在大脑中逐渐形成空间感，见图1。

图1

画图能让学生懂得画图的妙用，培养其空间立体感。需要时，各种立体图形的特征像放电影一样，在学生脑海中逐一呈现，为进一步学好立体几何打好基础。

二、画图，联系生活

长方体、正方体、圆柱体和图锥体都有各自的基本特征。但是，生活中各种几何图形的表面积、体积、容积、底面积、占地面积等，往往使学生混淆不清，误把占地面积当表面积，表面积看作体积，这种状况比比皆是。那么，如何快速、有效地解决这样的数学问题呢？只要让学生联系生活进行画图分析，这些问题就能迎刃而解。

例如，教学“占地面积”时，让学生先观察，然后教学生画图。学生很快就理解了教学要点，在圆柱体底部画上阴影，表示占地面积（见图2），计算后得出的面积为3.14×42=3.14×16=50.24（cm2）。

又如，计算长方体的表面积时会遇到多种情形，有时长方体上面无面，如玻璃鱼缸；有时长方体前后无面，如火柴盒……在学生不知道怎样灵活运用时，画图可以有效解决这一难题，也是一种简单、易行的好方法。如课桌长70cm，宽50cm，高40cm，求制作这张课桌需多少平方厘

图3

由上述例题不难看出，画图学几何简单、快捷，既能用数学解决生活中的实际问题，又能让学生尝到学数学的乐趣。

三、画图，培养思维

小学数学教学的重要目标之一是培养学生良好的思维能力。空间思维能力的培养绝不是凭空想象，更不是玩数学对对碰的游戏，只有勤于动手画图，才能有意想不到的效果。不妨来看两个例题。

例1：把一个底面边长是3cm的正方形的长方体切成3段，表面积增加了多少平方厘米？

例2：把一个底面半径3cm的圆柱切成4段，表面积增加了多少平方厘米？

在日常教学过程中，教师往往告诉学生切一刀增加2个面，拼一下减少2个面。但是，仅靠单纯地说教、灌输，学生很容易忘记。因此，要想让学生产生思维的火花，实际操作必不可少。笔者发现，通过图示对比能有效培养学生的思维能力。图4、图5分别是上述两个例题的图示。

图4

例1通过图示对比，学生很快发现共增加4个面，并做上“√”记号，增加的面积为3×3×4=36cm2。

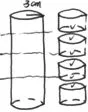
图5

例2通过图示对比，同样直观明了。通过底面、侧面比较，共增加6个底面，增加的面积为3.14×32×6= 169.56cm2。

因此，在具体的教学过程中，教师要指导学生学会画图，学会观察，学会思考。通过画图，不但能够帮助学生找到解决问题的途径，还能够突破数学理解上的难点。画图既培养了学生的思维能力，又让课堂教学收到了奇效。

四、画图，提升能力

培养学生运用数学知识解决实际问题的能力是义务教育阶段数学教学的重要目标之一。因此，解决实际问题在数学教学中有着重要的作用，它既是发展学生数学思维的过程，也是培养学生应用意识、创新意识的重要途径。

立体几何知识来源于生活。因此，学好几何知识，解决生活中的数学问题，成了小学数学的重中之重。一道道与现实生活紧密联系的几何题，是提升学生数学能力的精神食粮。如何把这种极佳的精神食粮为我所用，画图分析就是最好的方法。

例3：一个圆锥形沙滩，底面积28.26m2，高2.5m，用这堆沙在10m宽的公路上铺2cm厚的路面，能铺多少米？

对于这个与生活紧密相关的问题，仍然可以引导学生通过画图来解决。学生通过图示较快地掌握了数量关系，见图6。圆锥体变为长方体，虽然形状变了，但体积不变。设长为xm，计算公式为×28.26×2.5=10×0.02x，结果为117.75（m）。

图6

例4：一空容器A和装满水的容器B（见图7），把容器B的水倒一部分到A中，使两容器水一样高，A、B容器的水深各是多少？

图7

这也是一个与生活紧密联系的开放题，同样可以引导学生画图展示。学生很快发现了数量关系，原来B容器水的体积等于现在B容器水的体积+A容器水的体积，见图8。设A容器水深x，计算公式为40×30x+30×20x=30×20×24，x=8。因此，A、B容器的水深为8cm。

图8

这两道数学应用题，通过画图的形式渗透“数形结合”思想，使数学概念更具体、更简单，容易被学生接受。

立体几何学起来虽然很难，但养成画图的好习惯后，能使复杂而抽象的数学概念、数学关系变得形象而简单，为学生解决了学几何难的问题，还有利于培养学生的观察能力、提升学生的空间感，为学生学好小学立体几何奠定扎实的基础。小学立体几何，想说爱你也容易！

（编辑：易继斌）

中图分类号：G623.5

文献标识码：A

文章编号：1671-0568（2016）10-0065-02

作者简介：胡仁军，湖北省荆州市公安县育苗小学教师，公安县数学中心教研组成员，研究方向为小学数学。米的木板？（见图3）课桌少了一个面，用“x”做记号，让学生一目了然，计算后得出的面积为70×50×2+70×40+ 50×40×2=13800（cm2）。