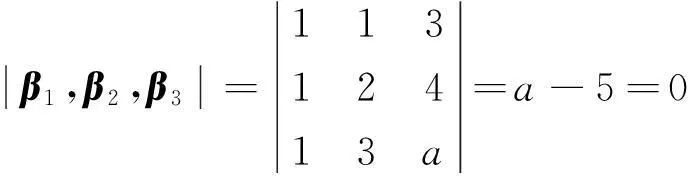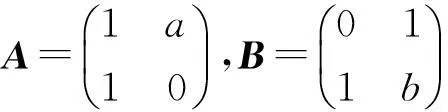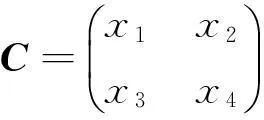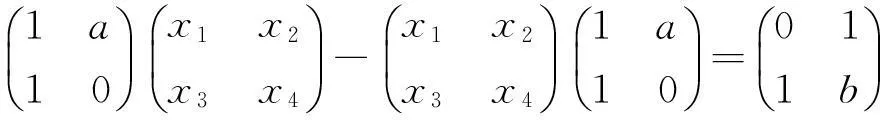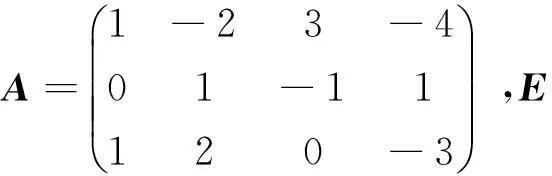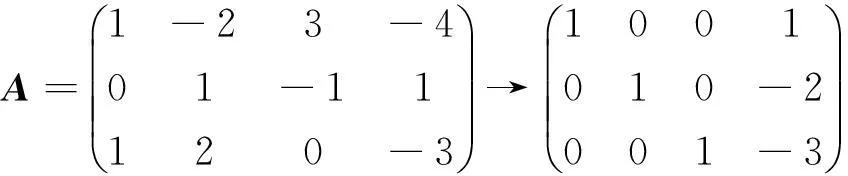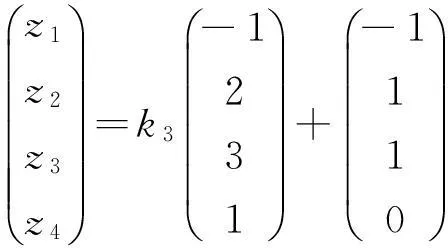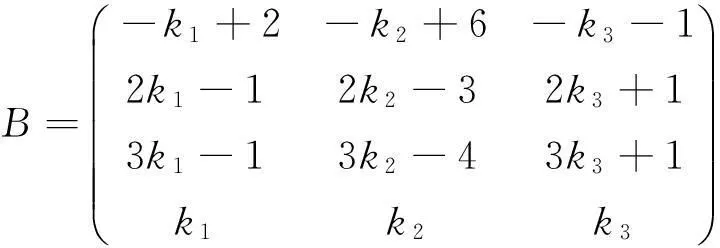线性方程组考研题型分析

王莲花

(北京物资学院 信息学院，北京 101149)



线性方程组考研题型分析

王莲花

(北京物资学院 信息学院，北京 101149)

摘要：分析近几年有关线性方程组考研试题，归纳相关题型及考核知识点，给出问题的一般解法，以期为学生考研复习、教师考研辅导及线性代数日常课堂教学提供参考.

关键词：线性方程组；初等变换；线性相关；线性无关

线性方程组是线性代数课程的核心内容之一，它是线性代数研究的具体模型.科学技术和经济管理中的许多问题，往往可以归结为建立线性方程组的问题．每年全国硕士研究生入学统一考试数学一(或二和三)试题均会在解答题中第(20)题以各种形式呈现线性方程组这一知识点，其分数均为11分，此外，有时还会配以选择题，可见其重要性．因此，考研学生必须高度重视，考研辅导老师也要作为考试重点给予针对性的辅导，其中对重要知识的讲解、解题思路的分析尤为重要．本文对有关线性方程组考研题型进行分类，并结合近几年数学考研试题进行剖析，以期为学生考研复习和教师考研辅导提供参考，同时也为讲授线性代数课程的教师提供指导．

1直接求线性方程组Ax=b的通解问题

这类考研题目往往系数矩阵中带有参数，其解决问题的方法有两种：初等行变换法和行列式法. 初等行变换法是利用初等行变换化方程组的增广矩阵为行阶梯矩阵，然后根据线性方程组有解判定定理确定方程组中的参数取何值时方程组有解，在有无穷多解时，求出方程组的通解．而行列式法则仅适合方程的个数与未知数的个数相等的情形，此方法是先计算系数行列式，然后根据参数的取值来进一步讨论方程组解的问题．看下面的两个例子．

例1设

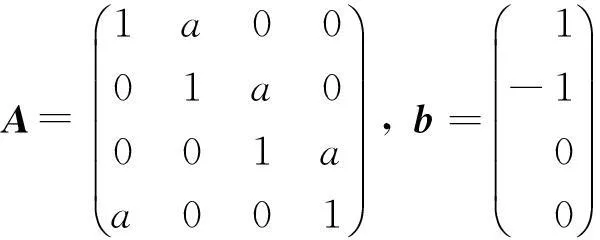
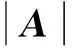
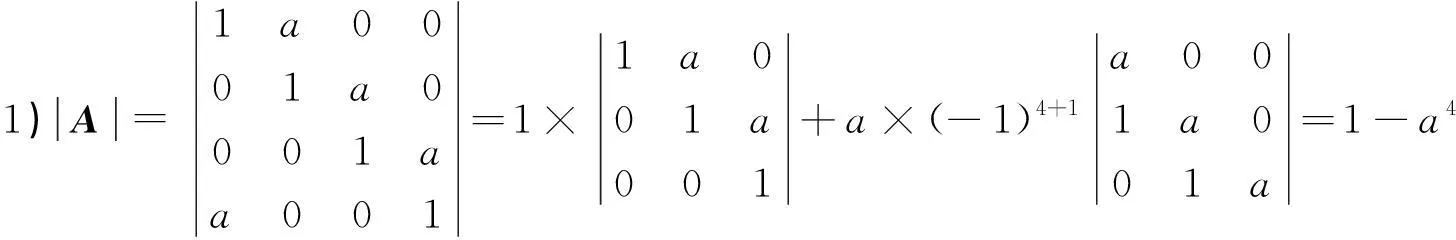
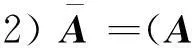
可知要使原方程组有无穷多解，必须使1-a4=0及-a-a2=0，得到a=-1.

此时原方程组的增广矩阵为

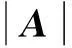
例 2 设矩阵

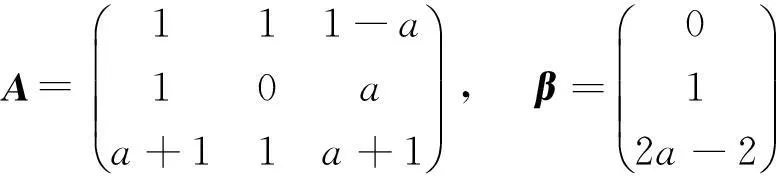
且方程组Ax=β无解，1)求a的值；2)求方程组AΤAx=AΤβ的通解[2].

分析 由于该方程组是3个方程3个未知数，且系数中带有参数，所以解此方程组时两种方法均可采用，但结合问题2)，该题采用行列式法比较简单.

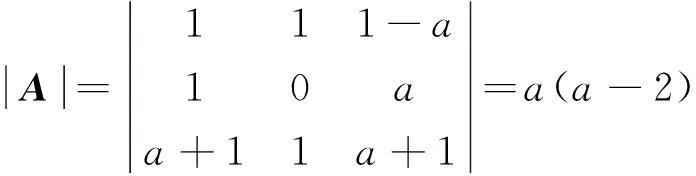
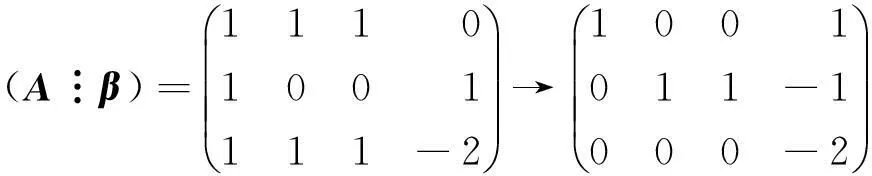
知， r(A)=2≠r(A⋮β)=3，方程组Ax=β无解.

当a=2时，

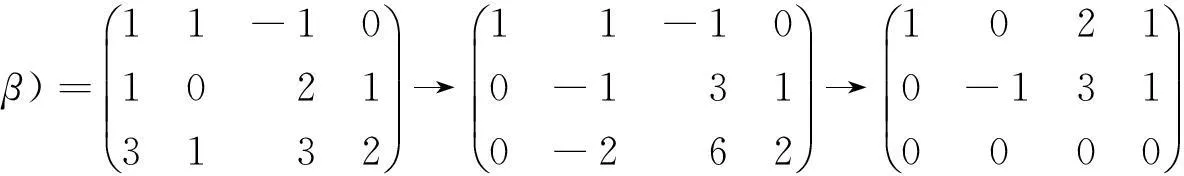
此时，r(A)=r(A⋮β)=2<3，方程组有无穷多解.故a=0.

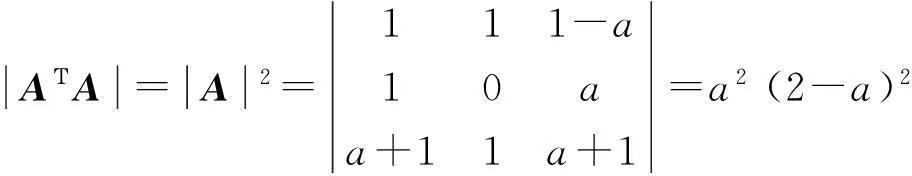
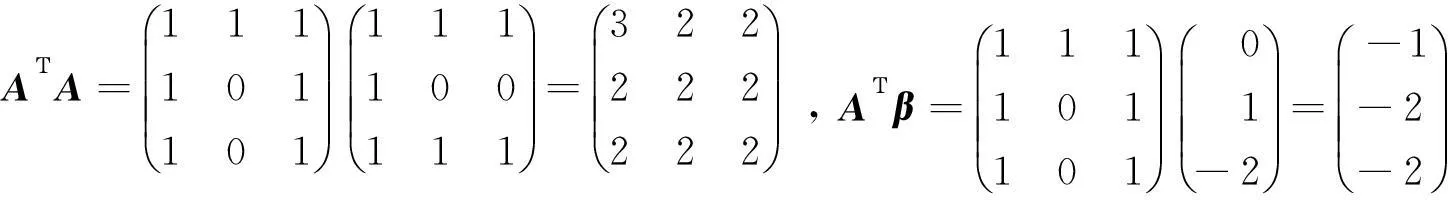
由

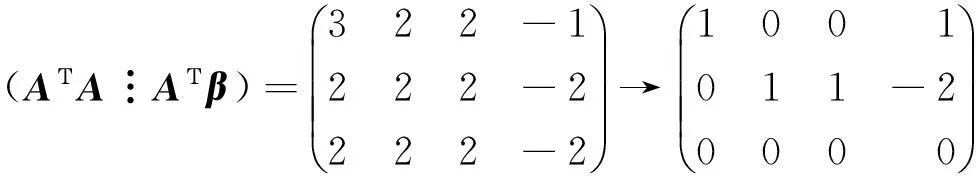
当a=2时，

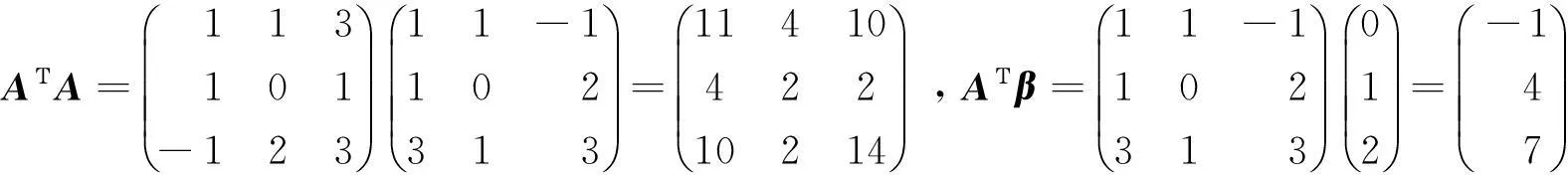
由

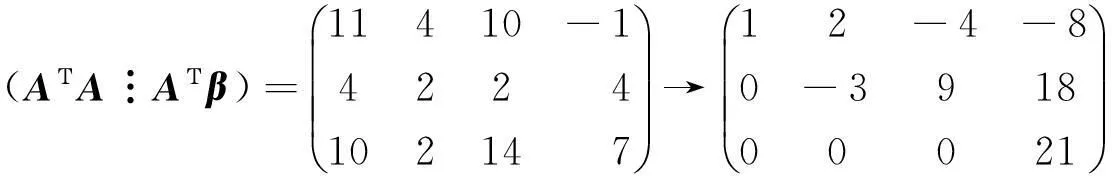
此时，r(A)=r(A⋮β)=2<3，方程组无解.

2求线性方程组Ax=b的一般解，并结合向量组的线性相关性问题

这类考题除按照通常求解线性方程组一般解的方法外，还需要掌握判定线性向量组线性相关性的方法．判定n维向量组α1,α2,…,αs线性相关性的常见方法有如下几种.

方法1定义法. 设k1α1+k2α2+…+ksαs=0，则α1,α2,…,αs线性相关的充要条件是该齐次线性方程组有非零解；α1,α2,…,αs线性无关的充要条件是该齐次线性方程组只有零解.

方法2求秩的方法.设A=(α1,α2,…,αs)，则α1,α2,…,αs线性相关的充要条件是r(A)

方法4设n维向量组α1,α2,…,αs，若s>n，则向量组α1,α2,…,αs线性相关.

例3设

1)求满足Aξ2=ξ1,A2ξ3=ξ1所有向量ξ2,ξ3；2)对1)中的任意向量ξ2,ξ3，证明：ξ1,ξ2,ξ3线性无关[3].

分析该题主要考核3个知识点：一是矩阵的乘法(乘幂)运算；二是线性方程组一般解的求法；三是n个n维向量组线性相关性的判别方法：行列式法．这些都是线性代数的基本理论和基本方法，考研的同学应该熟练掌握．

解 1)对增广矩阵(A⋮ξ1)施行初等行变换.

2)由1)知，

所以ξ1,ξ2,ξ3线性无关.

例4设向量组α1=(1,0,1)Τ,α2=(0,1,1)Τ,α3=(1,3,5)Τ不能由向量组β1=(1,1,1)Τ,β2=(1,2,3)Τ,β3=(3,4,a)Τ线性表出.

1)求a的值，2)将β1,β2,β3由α1,α2,α3线性表出[4].

分析首先，根据已知，判定向量组β1,β2,β3线性相关性，以确定参数a. 其次，利用向量的线性表示方法，即解非齐次线性方程组，求出线性表示式. 特别注意：这里还考核到一个重要结论：如果向量组α1,α2,…,αs线性无关，而向量组α1,α2,…,αs,β线性相关，则向量β必可由α1,α2,…,αs线性表示[5].

解 1)4个3维向量β1,β2,β3,αi线性相关(i=1,2,3). 若β1,β2,β3线性无关，则αi可由β1,β2,β3线性表示(i=1,2,3)，这与已知矛盾. 于是β1,β2,β3线性相关.从而

于是，a=5. 此时αi不能由β1,β2,β3线性表示.

2)令A=(α1,α2,α3⋮β1,β2,β3)，对A施行初等行变换

从而β1=2α1+4α2-α3,β2=α1+2α2,β3=5α1+10α2-2α3.

3利用解线性方程组求满足等式关系的未知矩阵

此类问题往往给出一个矩阵方程，然后根据已知矩阵求出未知矩阵．这种矩阵方程一般不能由可逆矩阵直接求出未知矩阵，而是需要设出未知矩阵，根据已知等式关系转化成非齐次线性方程组，然后利用求齐次非线性方程组一般解的方法求出未知矩阵．下面的例5和例6就是属于这种类型的考题．

即

所以

化简增广矩阵为

所以,当1+a=0,b=0，即a=-1,b=0时，矩阵C存在. 此时增广矩阵为

1)求方程组AX=0的一个基础解系；2)求满足AB=E的所有矩阵B[7].

解 1)对方程组的系数矩阵作初等行变换，得

令x4=1，得方程组AX=0的一个基础解系为α=(-1,2,3,1)Τ，其全部解为kα=k(-1,2,3,1)Τ，k为任意常数.

相当于

综上所述，解线性方程组是全国研究生入学统一考试数学试题每年必考到的内容，而且常常是以解答题的形式呈现，这类题目不仅涉及行列式和矩阵的基本知识，而且还与向量组的线性相关性理论等知识紧密相连，考生要想做好此类题，必须熟练掌握以下几方面的基本内容和做题方法：①简单行列式的计算；②矩阵的乘法；③利用初等行变换化非齐次线性方程组的增广矩阵为行阶梯矩阵或行最简矩阵的方法及线性方程组解的结构理论；④向量组线性相关性的一些重要判定方法. 同时，还要具有较扎实的基本功和灵活的解题技巧，以确保在计算时既快又准，只有这样，才能取得理想的成绩.

参考文献

[1]文都教育.2012年全国研究生入学统一考试数学三试题[EB/OL].[2016-01-03].http://www.chinakaoyan.com/info/article/id/18551.shtml.

[2]万学教育.2016年全国研究生入学统一考试数学三试题[EB/OL].[2015-11-02].http://edu.qq.com/a/20151227/014535.htm#p.

[3]中国教育在线考试频道.2009年全国研究生入学统一考试数学三试题[EB/OL].[2015-11-02].http://kaoyan.eol.cn/math_3947/20091113/t20091113_421083_4.shtml.

[4]文都教育.2011年全国研究生入学统一考试数学三试题[EB/OL].[2015-11-02].http://www.233.com/kaoyan/math/zhenti/20110117/150917913-6.html.

[5]杨子胥. 高等代数习题解[M].济南：山东科学技术出版社，2002.

[6]跨考教育.2013年全国研究生入学统一考试数学三试题[EB/OL].[2015-11-03]http://kaoyan.eol.cn/shuxue_3976/20130106/t20130106_890383_3.shtml.

[7]新东方在线.2014年全国研究生入学统一考试数学三试题[EB/OL].[2015-11-03]http://kaoyan.koolearn.com/20131227/801315_3.html.

Topic Analysis on System of Linear Equations of the National Master’s Entrance Examination

WANG Lianhua

(College of Information, Beijing Wuzi University, Beijing 101149, China)

Abstract:The test questions on system of linear equations of the national master’s entrance examination are analyzed. The related topic and the test of knowledge points are summarized, and give general solution of the problem, in order to provide references for the students review of postgraduate exam, teacher guidance of postgraduate exam and the daily classroom teaching of liner algebra.

Key words:system of linear equations; elementary transformation; linear dependence; linear independence

收稿日期：2016-01-22

基金项目：039专业建设—专业群建设(市级)(PXM2015_014214_000039)；2015年北京物资学院教学质量工程项目(项目分类编号及名称：7-1 教学团队建设)

作者简介：王莲花(1964—)，女，河南宁陵人，北京物资学院教授，硕士生导师，主要研究方向：代数教学与研究.

doi：10.3969/j.issn.1007-0834.2016.02.012

中图分类号：G642.0;O172.2

文献标志码：A

文章编号：1007-0834(2016)02-0050-06