关于两个线性方程组同解问题教学的思考
2016-10-20李毛亲
李毛亲
(台州学院 数学与信息工程学院,浙江 临海 317000)
关于两个线性方程组同解问题教学的思考
李毛亲
(台州学院数学与信息工程学院,浙江临海317000)
探讨教学中如何引导学生理解和掌握线性方程组同解的问题。首先通过对消元法理解,得出两个线性方程组同解的充分条件;其次利用矩阵的初等变换和初等矩阵的知识,得出两个线性方程组同解的必要条件;再者,通过理解系数矩阵列向量组与同解的关系,给出求一个向量组的极大无关组的方法。最后是怎样从内积的角度去看待同解问题。
线性方程组;同解;行向量组;列向量组;极大无关组;内积
0 引言
关于线性方程组同解问题,无论是在《高等代数》还是在《线性代数》教科书中涉及的内容并不多,但是该问题的内涵和外延却非常丰富多彩。问题可分为两方面,一是内涵,即同解问题本身;二是外延,即与同解相关联的问题。在教科书[1]上,线性方程组的同解问题只是在第三章出现,经过本章的学习,学生对同解问题的认识是粗浅的。此后,随着矩阵,线性空间和欧氏空间的学习,通过教师的有意引导,可以使得学生对线性方程组同解的问题的认识一步步加深。
求解线性方程组时碰到的第一个问题是同解的充分条件,即为什么经消元法得到的线性方程组与原方程组同解。关于同解的必要条件是在掌握了向量组之间等价关系的概念之后得到的。在学习了矩阵的初等变换和初等矩阵以后,线性方程组同解的充分必要条件的证明就会显得轻松而自然。在求解向量组的极大无关组时,再次提到线性方程组的同解问题则可以使学生领略到同解的丰富含义。最后,随着欧氏空间的学习,可以再次从内积的角度去理解线性方程组的解以及同解的意义。这样,经过循序渐进地教学,必然会收到很好的效果。
设所讨论的线性方程组分别为

和

其中A=(aij)mn和B=(bij)sn,c=(c1,c2,…,cm)T,d=(d1,d2,…,dm)T,增广矩阵为分别A和B。
1 线性方程组同解的充分条件
设用消元法对线性方程组(1)进行变换得到(2)(S=m),则(2)的每一个方程都是(1)的某些方程的线性组合,所以(1)的解都是(2)的解。类似地,容易证明(1)的每一个方程也可以由(2)的某些方程线性表出,所以(2)的解也是(1)的解,于是(1)和(2)同解。得到结论:消元法把一个线性方程组变为与之同解的线性方程组。在此教学过程中,学生对于方程之间的线性表出与解之间关系的理解比较困难,所以对同解的理解也是感性的和初步的。在学习了向量组的等价以及矩阵的概念之后,对线性方程组作消元的过程,完全可以看做是对其增广矩阵作初等行变换的过程,而两组方程之间的线性关系变成了增广矩阵的行向量组之间的线性关系。所以用向量的观点来看待同解问题,相应的结论为:
如果在第三章[1](线性方程组)证明该定理,可能会造成学生理解的困难,所以我们有意识地将该证明放在第四章[1](矩阵)的学习之后,这样,不仅证明过程很容易,而且也会进一步加深学生对同解问题的理解(本文关于该定理的证明在第3节)。
2 线性方程组同解的必要条件

其中R(·)表示向量组或矩阵的秩。
定理2%设线性方程组Ax=c有解,若线性方程组Ax=c和Bx=d同解,则的行向量组等价。
注:定理2的前提条件“线性方程组Ax=c有解”是必不可少的,因为,两个线性方程组同解包含他们都无解的情形,此时他们的增广矩阵的行向量之间不一定有线性关系。
至此,得到了两个线性方程组同解的充要条件。
3 初等变换与初等矩阵——消元法的实质
定理1的证明如下:
设线性方程组(1)和(2)的增广矩阵的行向量组等价,则存在可逆矩阵P使得PA=B,Pc=d。设x0是(2)的解,则Bx=d,即PAx0=Pc。由于P可逆,所以Ax0=c,(2)的解都是(1)的解。类似可以证明(1)的解都是(2)的解,所以(1)和(2)同解。
4 从同解看系数矩阵的列向量的线性关系——求极大无关组
设矩阵A的列向量为α1,α2,…,αn,即A=(α1,α2,…,αn),A经过初等行变换变为B=(β1,β2,…,βn),其中β1,β2,…,βn为B的列向量,则齐次线性方程组Ax=0与Bx=0同解。这意味着x1α1+x2α2+…+xnαn=0<=>x1β1+x2β2+…+xnβn=0,即向量组α1,α2,…,αn与β1,β2,…,βn有完全相同的线性关系。所以,如果βi1,βi2,…,βir是向量组β1,β2,…,βn的极大无关组,则αi1,αi2,…,αir就是向量组α1,α2,…,αn的极大无关组,反之亦然。这就是我们通常求极大无关组的方法,也是我们在教学中强调的另外一句话:列向量作行变不改变其线性关系,这句话其实是对同解问题的另一种表达。
例4.1求向量组的一个极大无关组,并把不属于极大无关组的向量用极大无关组线性表出。其中,

容易看出,向量组β1,β2,β3,β4的极大无关组为β1,β2,β4,且β3=β1-5β2.由于向量组α1,α2,α3,α4与β1,β2,β3,β4有完全相同的线性关系,所以向量组α1,α2,α3,α4的极大无关组为α1,α2,α4,且α3=α1-5α2.
5 用内积的观点看线性方程组的同解
在欧氏空间,首先来看齐次线性方程组的同解问题,设齐次线性方程组Ax=0的系数矩阵的行向量为α1,α2,…,αm,则方程组可以写成
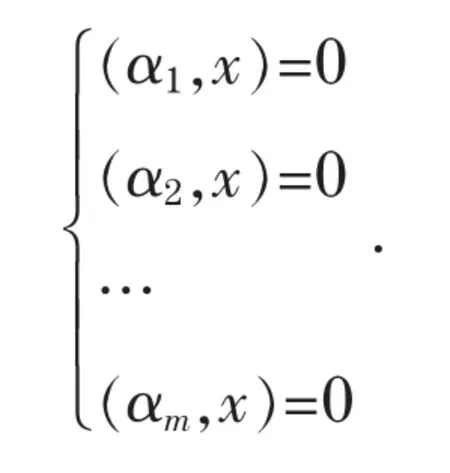
令W=L(α1,α2,…,αm)是由A的行向量组生成的子空间,则Ax=0的解空间就是(正交补)。设齐次线性方程组Bx=0的系数矩阵的行向量为β1,β2,…,βs,U=L(β1,β2,…,βs),则其解空间为。于是齐次线性方程组Ax=0与Bx=0同解的充要条件为,于是,W=U。由于两个生成子空间相等的充要条件是它们的生成元等价,所以得到结论:齐次线性方程组Ax=0与Bx=0同解的<=>其解空间相等<=>系数矩阵的行空间相等<=>系数矩阵的行向量组等价。
考虑到非齐次线性方程组解的结构,容易看出,Ax=c与Bx=d同解的充要条件是它们有一个公共解,且它们的导出组同解。于是在有解的前提下:Ax=c与Bx=d同解的充要条件是它们有一个公共解且系数矩阵A和B的行向量组等价。
例5.1条件如例4.1,求出子空间W=L(α1,α2,…,αm)的正交补空间。

基础解系为η1=(0,7,-18,16,3),η2=(1,8,-23,15,0),所以。
6 已知解,求方程组
纵观线性方程组的求解过程,就是一步步求解同解方程组的过程。最后得到的解事实上也是一个线性方程组(一种简单形式的线性方程组)。基于这样的观点,我们还可以解决这样的问题:求一个线性方程组,使得它的解是一组已知的向量。
例6.1α1,α2,α3,α4如例5.1所给,求以α1,α2,α3,α4为解的一个齐次线性方程组。
解:首先由例4.1知该向量组的极大无关组是α1,α2,α4,所以齐次线性方程组的基础解系为α1,α2,α4。再由例5.1,可知与α1,α2,α4等价的向量组为β1,β2,β4,所以,以它们为基础解系的齐次线性方程组同解,其中,。再写出β1,β2,β3以为基础解系的齐次线性方程组的全部解:

即
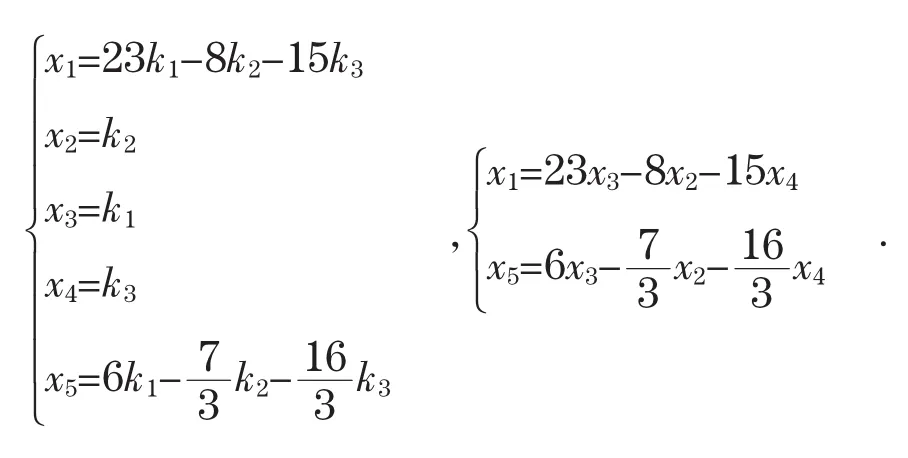
于是所求的齐次线性方程组为

注:由例5.1,W=L(α1,α2,α3,α4),W┸=L(η1,η2),而齐次线性方程组系数矩阵的行空间与解空间正交,所以,当系数矩阵的行向量为α1,α2,α3,α4,其解空间为W┸=L(η1,η2)。同理,当系数矩阵的行向量为η1,η2时,该齐次线性方程组的基础解系就是α1,α2,α3,α4的极大无关组α1,α2,α4。所以,所求的齐次线性方程组的系数矩阵为
例6.2求出以向量α1,α2,α3,α4为解的一个非齐次线性方程组。其中α1=(7,-8,2,1),α2=(8,-10,3,1),α3=(6,-6,1,1),α4=(2,-2,2,0)。
解:α1-α4,α2-α4,α3-α4为导出组的解,首先求出导出组的基础解系即向量组α1-α4,α2-α4,α3-α4的极大无关组为η1=α1-α4,η2=α2-α4。再求出与η1=(5,-6,0,1),η2=(6,-8,1,1)等价的向量组ξ1=(5,-6,0,1),ξ2=(1,-2,1,0)。于是所求的非齐次线性方程组的所有解为
[1]王萼芳,石明生.高等代数[M].(3版).北京:高等教育出版社,2013.
[2]同济大学.线性代数[M].(5版).北京:高等教育出版社,2007.
On the Teaching of Two System s of Linear Equations w ith Same Solutions
LIMaoqin
(School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China)
It is discussed that how to teach students to understand and master the problems about same solutions of two systems of linear equations.Firstly,the sufficient condition of same solutions problem is introduced by comprehending the elim ination.Secondly,the necessary condition of it is given by understanding elementary transformations and elementary matrices.Then,we give a w ay to find out maximal independent system s from the concept of the same solutions.Lastly,w e explore how to deal w ith the same solution problem s by scalar product in Euclidean spaces.
system of linear equations;same solution;row vector;column vector;maximal independent system; scalar product
10.13853/j.cnki.issn.1672-3708.2016.03.012
(责任编辑:耿继祥)
2016-01-22;
2016-05-15
李毛亲(1958-),女,山西太原人,副教授,硕士,主要从事运筹学及教学研究。
