次对合矩阵及其性质

周　涛

(重庆师范大学涉外商贸学院 数学与计算机学院, 重庆 401520)



次对合矩阵及其性质

周涛

(重庆师范大学涉外商贸学院 数学与计算机学院, 重庆 401520)

摘要：根据次对合矩阵的定义, 从一个实例出发, 讨论了实次对合矩阵的存在性, 最后给出了次对合矩阵的若干性质.

关键词：次单位矩阵; 次对合矩阵; 对角矩阵; 次对角矩阵; 张量积

1准备知识

本文用E表示单位矩阵；Jn表示次对角线元素为1，其余元素全为0的n阶方阵，称为n阶次单位矩阵, 在不引起混乱的情况下,也简记为J, 显然有J-1=J；A*表示矩阵A的伴随矩阵;A∈Pn×n表示数域P上的n阶方阵; N表示全体自然数之集;把对角矩阵

简记为diag{λ1,λ2,…,λn}.

定义1[1]对A∈Pn×n,若A2=E则称A为对合矩阵; 若A2=J,则称A为次对合矩阵.

定义2[2]设A是n阶方阵，若存在n阶矩阵B，使得AB=BA=J，则称B为矩阵A的次逆，记为A(-1)．

由定义1、2显然有, 若A是次对合矩阵, A一定是可逆矩阵. 若A是次可逆矩阵, 则一定有AJ=JA；且容易证明次可逆矩阵一定可逆.

定义3[3]设矩阵A=(aij)m×n,B=(bij)p×q，则mp×nq矩阵

称为矩阵A和B的张量积，记为A⊗B．

引理1[4](Laplace定理)设在行列式D中任意取定了k(1≤k≤n-1)个行, 由这k行元素所组成的一切k级子式与它们的代数余子式乘积之和等于行列式D.

2实次对合矩阵的存在性讨论

在文献[1]中, 给出了一些实次对合矩阵的有关结论. 但是在讨论中, 发现次对合矩阵并不像对合矩阵那么简单, 显然存在任意节的实对合矩阵, 但并不是任意阶实次对合矩阵都存在, 首先，我们很容易得到下面这个结论.

结论1不存在2阶实次对合矩阵.

由此可知, 不是任意阶实次对合矩阵都存在, 那么阶数n满足什么条件, 才存在实次对合矩阵呢?

定理1设A∈Rn×n(即n阶实方阵), 当n=4k+2或n=4k+3(k∈N)时, A一定不是次对合矩阵, 换句话说, 不存在4k+2,4k+3(k∈N)阶实次对合矩阵.

证明当n=4k+3时, 首先讨论n阶次单位矩阵J的特征值, J的特征多项式为

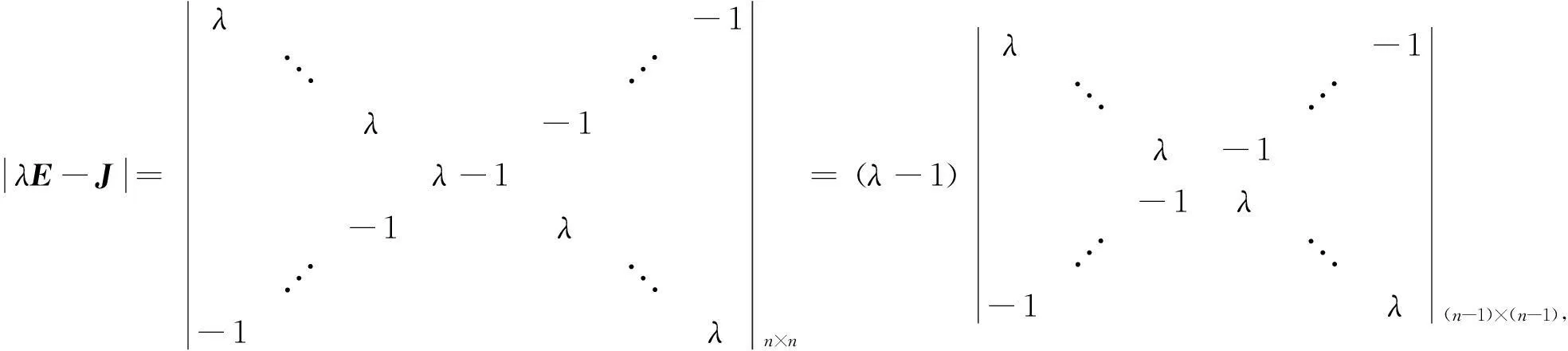
由Laplace定理,

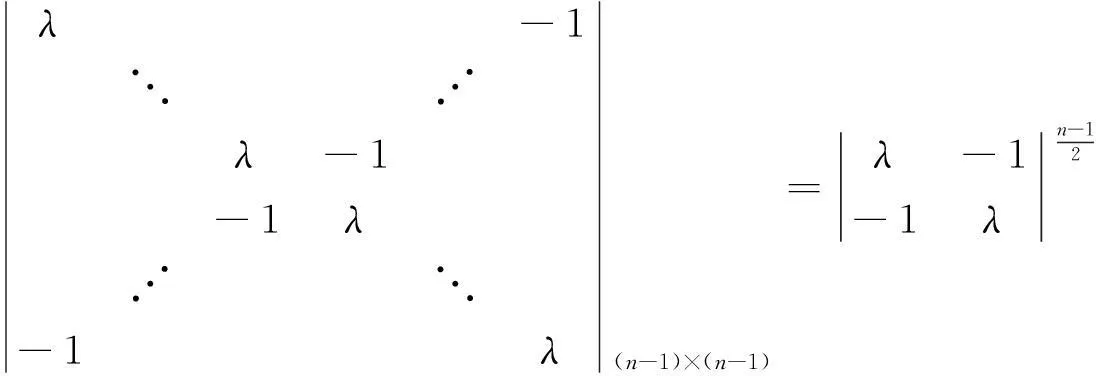
若A2=J, 则A的特征值只能为1,-1,i,-i,其中1，-1的个数之和是2k+2,i与-i个数之和为2k+1, 它们是A的全部特征值, 于是它的特征多项式为

f(λ)=(λ-1)r1(λ+1)(2k+2)-r1(λ-i)r2(λ+i)(2k+1)-r2,

显然f(λ)不是实多项式, 而A是实矩阵,它的特征多项式一定是一个实多项式, 矛盾, 所以不存在4k+3阶实次对合矩阵.

当n=4k+2时, 用同样的方法可得J的特征值为1(2k+1重), -1(2k+1重), 于是,若A2=J,可得到A的特征多项式不是实系数多项式, 与A是实矩阵矛盾.

综上, 不存在4k+2,4k+3(k∈N)阶实次对合矩阵.

由定理1知, 不存在4k+2,4k+3(k∈N)阶实次对合矩阵, 那么对于其他阶数的方阵,实次对合矩阵是不是存在？下面以4阶为例, 说明这样的实次对合矩阵是存在的.

例1求一个4阶实次对合矩阵.

则有T-1JT=diag{1,1,-1,-1}.

另一方面,容易得到

于是记

则A2=J, 即A即是一个4阶实次对合矩阵.

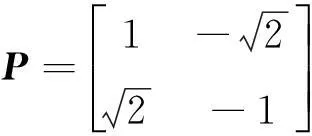
由此可得以下定理:

定理2一定存在4k+1,4k+4(k∈N)阶实次对合矩阵.

以上两个定理不仅给出了实次对合矩阵的存在性, 并给出了在存在的情况下, 次对合矩阵的求法, 显然如果在复数域内, 次对合矩阵的存在性变得更简单了, 即存在任意阶复次对合矩阵. 3次对合矩阵有如下性质.

性质1若A是次对合矩阵, 则AT,A-1都是次对合矩阵.

证明 (AT)2=(A2)T=JT=J;(A-1)2=(A2)-1=J-1=J.

性质2 设A是n阶方阵, 若n=4k,4k+1时, A*也是次对合矩阵.

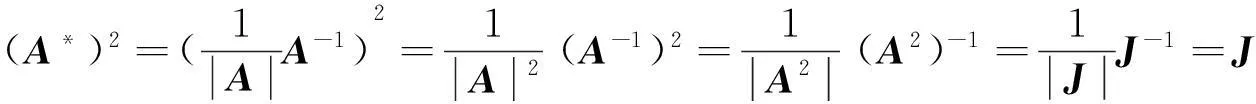
所以A*是次对合矩阵.

性质3若A是次对合矩阵，T是次可逆矩阵，则B=T-1AT是次对合矩阵.

证明由T可逆知: TJ=JT, 又因为A是次对合矩阵, 所以A2=J. 于是B2=(T-1AT)2=T-1A2T=T-1JT=T-1TJ=EJ=J,所以B是次对合矩阵.

性质4设A,B都是n阶方阵, 且AB=BA,

1)若A,B都是次对合矩阵, 则AB是对合矩阵;

2)若A是次对合矩阵, B是对合矩阵, 则AB是次对合矩阵.

证明1)、2)证明方法相同, 这里只证1), 由条件知: A2=J,B2=J,且AB=BA,于是

(AB)2=A(BA)B=A(AB)B=(AA)(BB)=J2=E,

所以AB是对合矩阵.

推论设A,B都是n阶方阵, 且AB=BA,

1)若A,B都是次对合矩阵, 则(AB)k(k为正整数)是对合矩阵;

2)若A是次对合矩阵, B是对合矩阵, 则ABk(k为正整数)是次对合矩阵.

性质5设A,B分别是m,n级次对合矩阵，则A⊗B是mn级次对合矩阵.

证明因为A2=Jm,B2=Jn，于是(A⊗B)2=A2⊗B2=Jmn，故A⊗B是mn级次对合矩阵.

参考文献

[1]陈湘赟. 次对称矩阵的一些性质[J]. 盐城工学院学报，2007，20 (4):17-18.

[2]刘玉, 陈创鑫. 次可逆矩阵及其性质[J]. 大学数学,2010,26(3): 177-180.

[3]许甫华, 张贤科. 高等代数解题方法[M]. 2版.北京：清华大学出版社，2014：504-505.

[4]北京大学数学系几何与代数教研室前代数小组.高等代数[M].3版. 王萼芳, 石生明，修订.北京：高等教育出版社， 2007：89-92.

Sub-involutory Matrix and Its Properties

ZHOU Tao

(School of Mathematics and Computer, Foreign Trade and Business College of ChongqingNormalUniversity,Chongqing401520,China)

Abstract:According to the definition of sub-involutory matrix and on the basis of an example, discuss the existence of the sub-involutory matrix, and give some properties of sub-involutory matrix.

Key words:sub-identity matrix; sub-involutory matrix; diagonal matrix; sub-diagonal matrix; tensor product

收稿日期：2015-11-15

作者简介：周涛(1986—)，男，河南驻马店人，重庆师范大学涉外商贸学院数学与计算机学院讲师.

doi：10.3969/j.issn.1007-0834.2016.02.003

中图分类号：O151.21

文献标志码：A

文章编号：1007-0834(2016)02-0010-03