随机代数Riccati方程的向后误差分析

肖玲莉, 邱本花,赵　冰

(1.郑州科技学院 基础教学部，河南 郑州 450064; 2.中州大学 信息工程学院，河南 郑州 45000)



随机代数Riccati方程的向后误差分析

肖玲莉1, 邱本花1,赵冰2

(1.郑州科技学院 基础教学部，河南 郑州 450064; 2.中州大学 信息工程学院，河南 郑州 45000)

摘要：利用矩阵Kronecker 积的性质和不动点定理，研究了随机代数Riccati方程的向后误差问题，给出了矩阵方程向后误差的上界和下界，并利用隐函数定理，得出了向后误差的一阶近似估计，最后用数值算例验证了结果的精确性.

关键词：随机代数Riccati方程；向后误差；Kronecker 积；不动点定理

0引言

在现代控制理论和其他工程领域，特别是在线性二次型最优控制系统、线性最优滤波系统的分析、综合和设计中,Riccati方程都起着非常关键的作用[1-5].对一般代数Riccati方程向后误差的研究已有大量文献[6-8]，但对随机代数Riccati方程向后误差的研究极少.本文主要对随机代数Riccati方程进行分析，估算出了该方程极大解的向后误差的上下界.

考虑随机代数Riccati方程(SARE):

ATX+XA+CTXC-(XB+CTXD)(R+DTXD)-1(BTX+DTXC)+Q=0，

(1)

其中R+DTXD>0，A,B,C,D,R,Q是常数矩阵，A,C∈Rn×n,B,D∈Rn×m，R∈Sm，Q∈Sn.

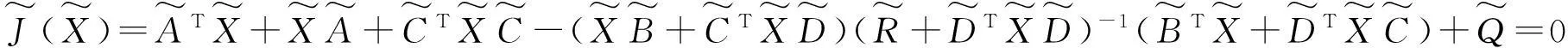
(2)

其中

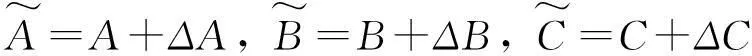
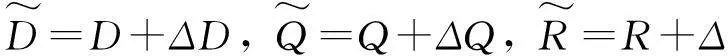
定义方程的向后误差为

(3)

其中Ax，Bx，Cx，Dx，Qx，Rx是大于0的参数.

vec(XT)=∏vec(X),EYF=P⟺(FT⊗E)vec(Y)=vec(P).

1.1方程(2)的等价形式

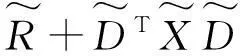
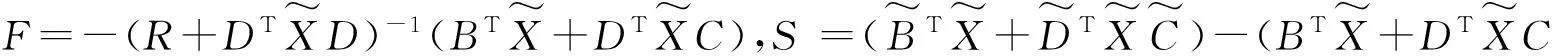
方程(2)等价于

(4)

再利用矩阵关系式

(I+M-1N)-1=I-M-1(I+NM-1)-1N=I-(M+N)-1N,

(M+N)-1NM-1=M-1N(M+N)-1.

得

FTGF+(S+GF)T(R+DTXD+G)-1(S+GF).

(5)

由于

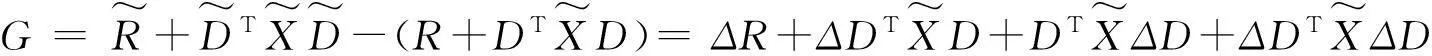
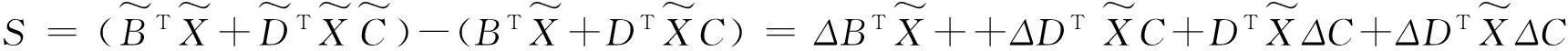
结合(5)式，方程(4)可等价变形为

(S+GF)T(R+DTXD+G)-1(S+GF)=-E,

即

FTΔRF+ΔQ-(S+GF)T(R+DTXD+G)-1(S+GF)=-E.

(6)

其中

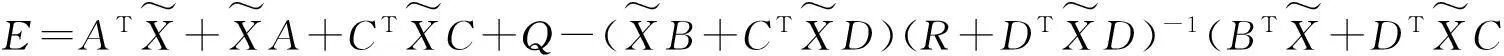
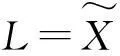
方程(6)等价于

L+LTΔC+FTΔDTL+LTΔDF+FTΔRF+ΔQ=-E+ћ(ΔX),

(7)

其中

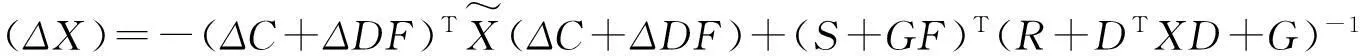
由引理1知， 方程(7)可以写成如下的非线性形式

T·g=-vecE+vec (ћ(ΔX)),

(8)

记

T=(AxT1,BxT2,CxT3,DxT4,QxT5,RxT6),

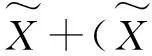
T3=I⊗LT+(LT⊗I)∏,T4=FT⊗LT+(LT⊗FT)∏,

T5=I⊗I,T6=FT⊗FT.

(9)

由(9)式中T的表达式可知T是行满秩矩阵， 故矩阵T存在广义逆， 即存在T†满足T†T=TT†=I.

考虑方程

g=T†[-vecE+vec (ћ(ΔX))],

(10)

显然满足(10)的g也一定满足方程(7). 因此， 若存在一个g*=

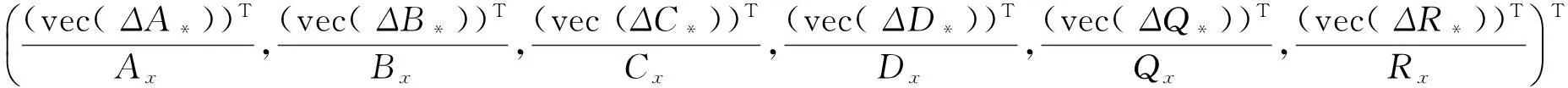
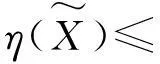
对(7)式两边取范数得

(11)

其中ρ，t定义如下

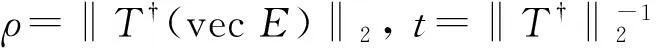
(12)

由于

(13)

且

‖S+GF‖≤ ‖ΔBTX+ΔDTL+ΔRF+DTXΔC+DTXΔDF‖+‖ΔDTXΔC‖+‖ΔDTXΔDF‖≤

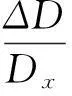
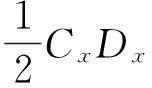
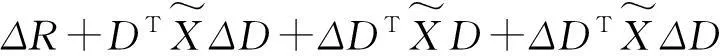
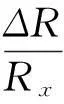
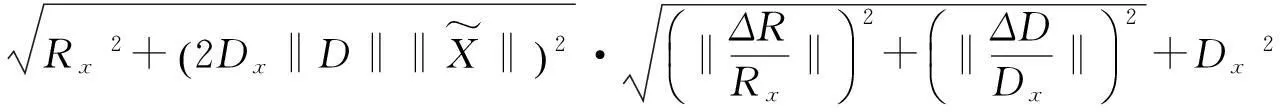
r3‖g‖+r4‖g‖2,

(15)

其中

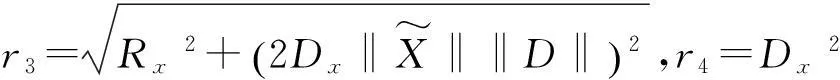
记

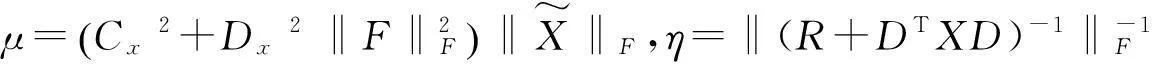
将(14)和(15)式代入(13)式， 得

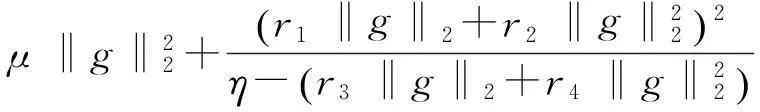
结合(11)式， 得到

其中ρ，t由式(12)定义.

考虑方程

整理变形得

(r22-μr4)x4+(tr4-μr3+2r1r2)x3+(tr3-ρtr4+ημ+r12)x2-(ηt+ρtr3)x+ρtη=0.

(16)

假设方程(16)的最小正实根为x*， 由不动点定理可知， 至少存在一个g满足(10)式， 且

‖g‖2≤x*.

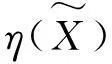
假设存在矩阵ΔAmin,ΔBmin,ΔCmin,ΔDmin,ΔQmin和ΔRmin使得

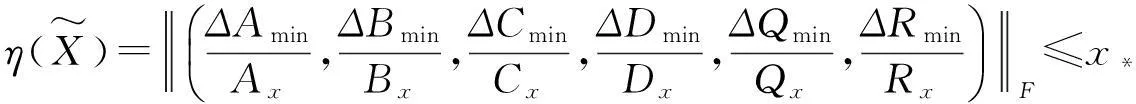
这里x*是方程(16)的最小正实根.由(8)式知矩阵ΔAmin,ΔBmin,ΔCmin,ΔDmin,ΔQmin和ΔRmin满足

Tgmin=-vec (E)+vec( ћ(ΔX)),

(17)

其中gmin=

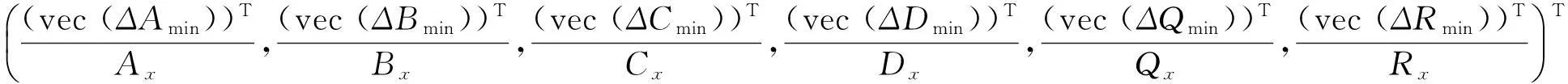
令

T=W(Σ，0)ZT,

(18)

其中

Σ=diag(ξ1,ξ2,…,ξn2),ξ1≥ξ2≥…≥ξn2>0.

W和Z是正交矩阵. 将(18)式代入(17)式中， 得

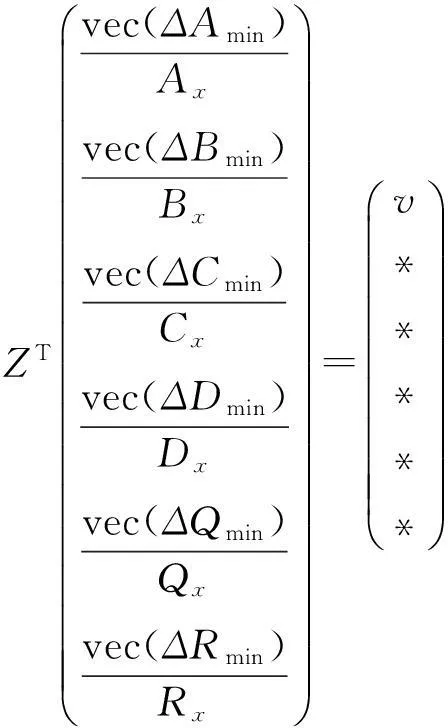
(19)

其中

v=-Σ-1WTvec(E)+Σ-1WTvec(ћ(ΔX)).

(20)

结合(17)～(20)式， 得到

‖T†(vecE)‖2-‖T†‖2‖ћ(ΔX)‖F≥

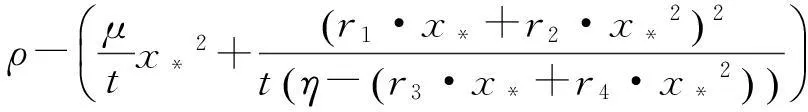
(21)

由于x*是方程(16)的最小正实根， 故有

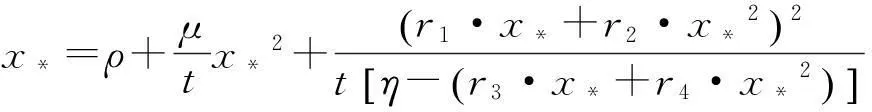
于是(21)式可简化为

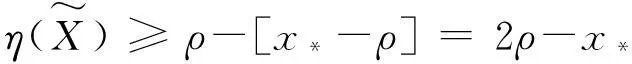
综上， 可以得到下述定理.

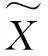
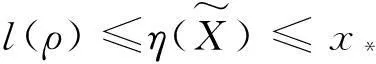
(22)

其中x*是方程(16)的最小正实根，ρ=‖T†(vecE)‖2，l(ρ)=2ρ-x*.

注 释记函数

F(x,ρ)=(r22-μr4)x4+(tr4-μr3+2r1r2)x3+(tr3-ρtr4+ημ+r12)x2-(ηt+ρtr3)x+ρtη，

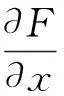
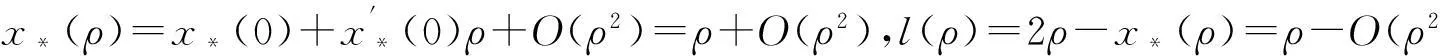
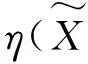
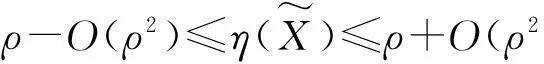
(23)

由于ρ=‖T†(vecE)‖2,且

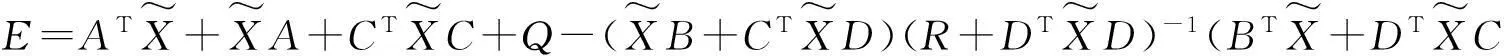
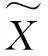
2数值实验

令

方程( 1)的系数矩阵A,B,C,D,R分别为

A=-4I20+3U,B=2I20-3U,C=I20,D=I20+U,R=3U.

Ax=‖A‖F，Bx=‖B‖F，Cx=‖C‖F，Dx=‖D‖F，Qx=‖Q‖F，Rx=‖R‖F.

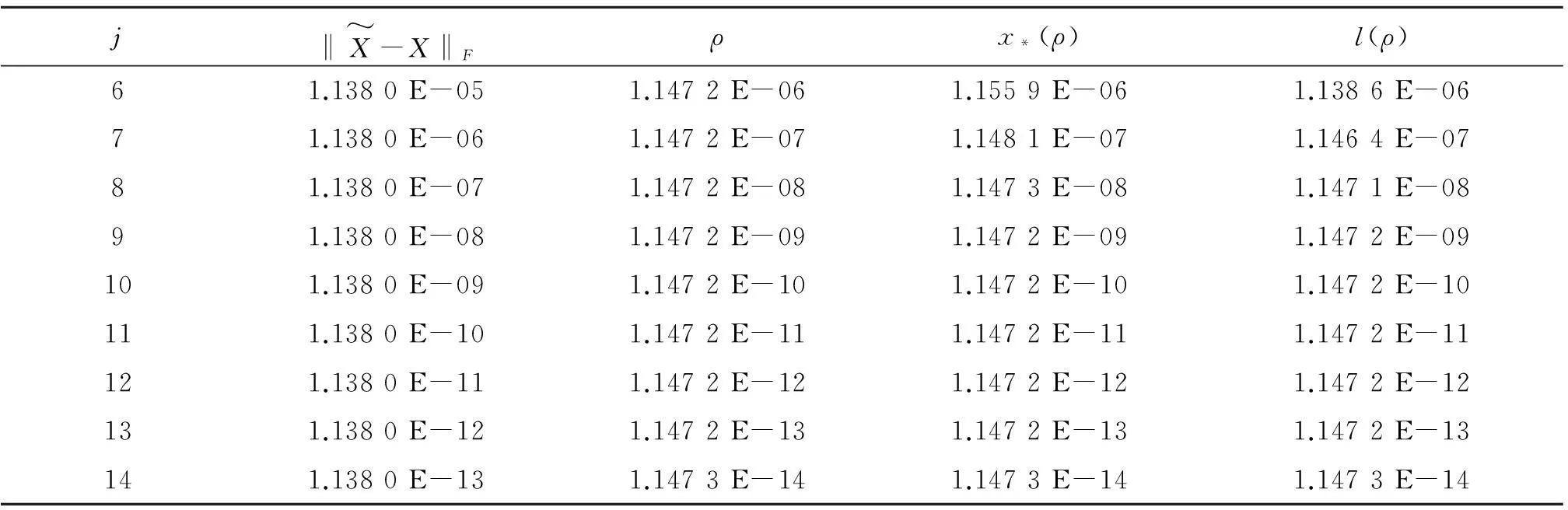
表1　一套实验数据和相应的模拟结果

3结论

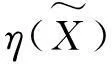
参考文献

[1]BOUHTOURI A E, HINRICHSEN D, PRITCHARD A J. On the disturbance attenuation problem for a wide class of time invariant linear stochastic systems[J].Stoch Rep, 1999, 65: 255-297.

[2]DAMM T, HINRICHSEN D. Newton’s method for a rational matrix equation occurring in stochastic control [J].Linear Algebra Appl, 2001, 332: 81-109.

[3]HINRICHSEN D, PRITCHARD A J. Stochastic H∞[J]. SIAM J Control Optim, 1998, 36: 1504-1538.

[4]GUO C H, HIGHAM N J. ITErative solution of a nonsymmetric algebraic Riccati equation[J]. SIAM journal on matrix analysis and applications, 2007, 29(2): 396-412.

[5]RAMI M A, ZHOU X Y. Linear matrix inequalities, Riccati equations, and indefinite stochastic linear quadratic controls [J]. IEEE Trans Automa Contr, 2000, 45:1131-1143.

[6]RIGAL L, GACHES J. On the computability of a given solution with the data of a linear system[J]. J Assoc Comput Mach, 1967, 14: 90-101.

[7]HIGHAM N J. Perturbation theory and backward error forAX-XB=C[J]. BIT Numerical Mathematics, 1993, 33(1): 124-136.

[8]KIGSTRIIM B. A perturbation analysis of the generalized Sylvester equation (AR-LB,DR-LE)=(C,F)[J]. SIAM J Matrix Anal AppZ, 1994, 15: 1045-1060.

[9]HORN R A, JOHNSON C R. Topics in matrix analysis[M]. New York: Cambridge UP, 1991.

Backward Error Analysis on the Stochastic Algebraic Riccati Equation

XIAO Lingli1, QIU Benhua1, ZHAO Bing2

(1. Department of Basic Courses, Zhengzhou University for Science and Technology , Zhengzhou 450064, China;2.DepartmentofInformationEngineering,ZhongzhouUniversity,Zhengzhou450000,China)

Abstract:By using the properties of Kronecker product and the fixed point theorem, the normwise backward error of the stochastic algebraic Riccati equation is studied. The upper and lower bounds of the backward error are given, and the first-order approximate estimates of the backward error are obtained by using the implicit function theorem, finally the accuracy of the result is verified with a numerical example.

Key words:stochastic algebraic Riccati equation； backward error； Kronecker product； fixed point theorem

收稿日期：2015-12-16

基金项目：郑州市科技局软科学项目(20141153)：河南省基础与前沿项目(152300410170)

作者简介：肖玲莉 ( 1990—)，女，河南信阳人，郑州科技学院基础教学部教师.

doi：10.3969/j.issn.1007-0834.2016.02.005

中图分类号：O224

文献标志码：A

文章编号：1007-0834(2016)02-0017-07