利用行列式、矩阵求解线性方程组
2017-05-15付美鑫
付美鑫
(长春汽车工业高等专科学校,长春 130607)
利用行列式、矩阵求解线性方程组
付美鑫
(长春汽车工业高等专科学校,长春 130607)
行列式、矩阵在线性代数中占有十分重要的地位,尤其对于求解线性方程组,不仅使计算简便,更使结果一目了然。本文主要讨论利用行列式、矩阵求解线性方程组的方法。
行列式;矩阵;线性方程组
对于线性方程组的求解,随着未知量的增加和方程个数的增加,计算也越来越难,基本的消元法已不能满足一般的线性方程组的求解。但是利用行列式、矩阵求解,可以相对简化计算,对于更复杂的线性方程组,也可以按照此方法通过计算机来实现。以下介绍如何用行列式、矩阵来求解线性方程组。
1 行列式法求解线性方程组
行列式法求解线性方程组,主要是利用克莱姆法则进行计算。
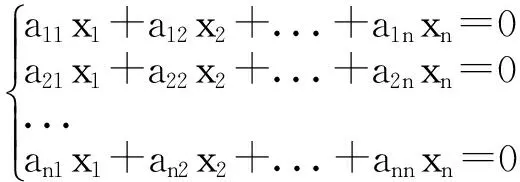
克莱姆法则:n个未知量,n个方程的线性方程组
(1)
这里要注意的是n个未知量,n个方程,这是因为对于行列式而言,都是n行n列的,其次要注意的是必须满足系数行列式D不等于0,当系数行列式D=0时,则该方程组至少有两个解或者无解。
于是
2 利用矩阵计算线性方程组
2.1 逆矩阵法解方程组

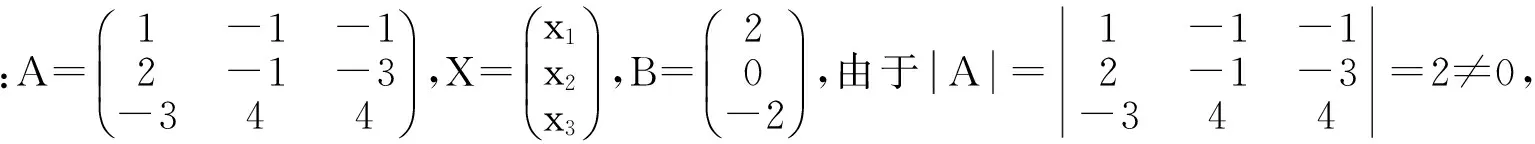
该方法适用于未知量和方程数相等的线性方程组,也适用于方程数小于未知量的情况。该方法是将线性方程组的增广矩阵通过行变换化为行最简形,得到同解方程组,从而确定约束未知量和自由未知量。这里约束未知量是指行最简形主元为1对应的未知量,其余的称为自由未知量,然后设自由未知量为任意常数,用自由未知量表示约束未知量,从而得到方程的通解。
解法一:将非齐次线性方程组的增广矩阵化为行最简
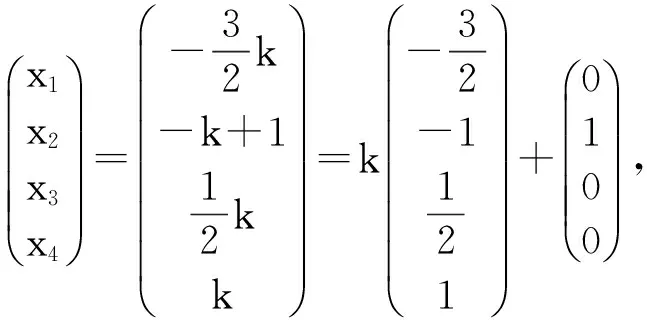
该题也可以用线性方程组解的结构来做,非齐次线性方程组的解等于对应齐次线性方程组的通解加上非齐次线性方程组的一个特解。
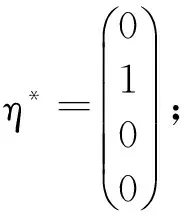
故齐次方程组的通解为
从而原非齐次线性方程组的通解为
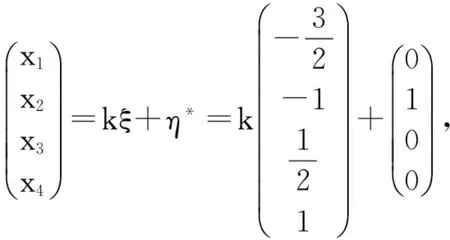
[1] 林清.矩阵在解线性方程组中的应用[J].科技研究,2014,(11):85-86.
[2] 谭高山,汪忠志.线性代数课程教学的实践与思考[J].安徽工业大学学报(社会科学版),2014,(04):92-97.
[3] 贾敬堂,李玉海,史裕曙.高职教学行列式的计算方法及应用[J].邯郸职业技术学院学报,2013,(03):76-79.
[4] 李文友.研究线性方程组的简便方法[J].天中学刊,2002,(02):54-55.
Solving linear equations by using determinant and matrix
FU Mei-xin
(Changchun Automotive Industry College, Changchun 130607, China)
Determinant and matrix occupy very important position in linear algebra, especially for solving linear equations, which not only makes the calculation simple, but also make the results at a glance. This paper mainly discusses the method of solving linear equations by using determinant and matrix.
Determinant; Matrix; Linear equations
2016-12-06
付美鑫(1988-),女,助教,硕士。
O151
B
1674-8646(2017)03-0072-02
