卷积码识别算法浅述
2016-07-07丁峤,徐卫
丁 峤,徐 卫
(1.解放军理工大学,南京 210007;2.空军通信网络技术管理中心,北京 100843)
卷积码识别算法浅述
丁峤1,徐卫2
(1.解放军理工大学,南京 210007;2.空军通信网络技术管理中心,北京 100843)
摘要:本文介绍了信道编码识别技术的发展概况,给出了常规识别算法、基于校验矩阵识别算法和基于欧几里德识别算法三种卷积码识别算法的工作原理,对比分析了三种算法的性能。
关键词:卷积码;编码识别;校验矩阵;欧几里德算法;算法性能
徐 卫,空军通信网络技术管理中心高级工程师,主要从事通信网络管理方面的技术工作。
1 引言
通信侦察使用专门的侦察设备搜索、截获无线电通信信号,通过对信号进行处理、分析和识别,从而获取大量通信对抗情报,乃至重要的军事情报。由于不同通信系统的业务要求和信道条件差异较大,因此,不同的通信系统通常采用不同的信道编码方案,这对于诸如通信侦察这样的非合作通信来说,要获取无线电信号中所携带的信息,知道该信号所采用的信道编码方案是其中的必要条件之一,编码分析识别技术在通信侦察领域应运而生。此外,编码分析识别技术还可以应用于未来智能通信领域、无线电监测与管理等领域[1]。
2 信道编码识别技术发展概况
当前信道编码分析识别技术研究主要集中在对线性分组码和卷积码的盲识别上。
二进制线性分组码的盲识别方法又可分为通过解线性方程来计算校验多项式的识别方法和基于码组正交空间的盲识别方法。利用低码率二进制线性分组码的码重分布特征来估计编码参数[2],数据矩阵求秩的方法在无误码情况下能够准确地估计出线性分组码码长、码组偏差,但是当误码率较高时,由于矩阵求秩的限制,不能有效估计出编码参数,并且,当码长较长时,也不能有效估计出编码参数。
RS码的盲识别方法是基于伽罗华域傅立叶变换来实现的,它是利用RS码在伽罗华域中的零谱连续特征求出码根,得到编码参数。卷积码的盲识别方法可进一步分为一般卷积码的盲识别和删除卷积码的盲识别方法。当前编码盲识别技术尚处于发展中,仍存在许多局限和不足。本文主要介绍卷积码的盲识别算法。
3 常见卷积码识别算法
3.1 常规识别算法
进行卷积码识别最直接的算法是求解线性方程组。为叙述简单,我们以码率为 的卷积码为例。设卷积码是[4]
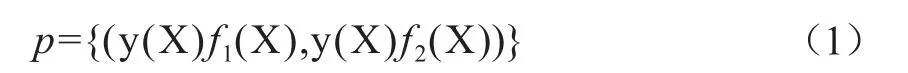
式中,y(X)=y0+y1X+y2X2+…,是信息源数据序列;f1(X),f2(X)是生成多项式。p(X)=(p1(X),p2(X))∈p,其中,pi(X)= pi , 0+ pi , 1X+ pi , 2X2+…,i = 1 , 2。该方法需要先估计约束长度L=max(degf1(X),degf2(X))。如果能保证采集到的不含误码的卷积码的片段序列足够长N≥3(L+1),即要获取的卷积码码流比特数大于2N=6(L+1),则可以求解如下的线性方程组:
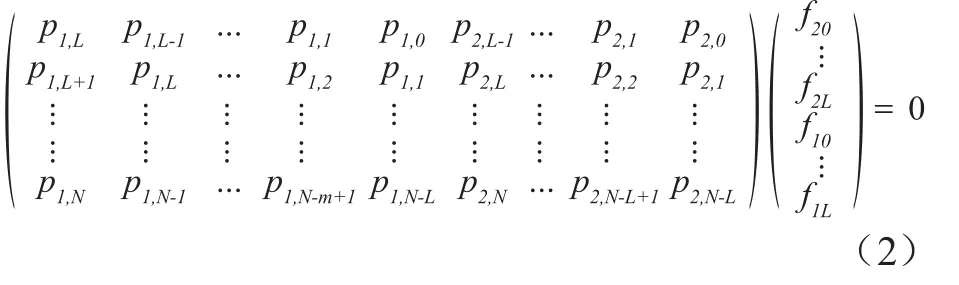
常规做法是高斯消元法,但是会存以下弊端:
首先,高斯消元法是不容错的,即要求方程组(2)中的系数矩阵中的每个系数不能有错误。但在实际通信中,信道误码在所难免,采集到的数据很难保证没有差错。
其次,为保证方程组(2)的可解性,要求卷积码序列长度N≥3(L+1)。由于L也是未知的,所以要设置一个较大的估计值,通常是实际约束长度的数倍,而且未知参数L与N是相同数量级,所以必须采集足够长的数据。同时方程组(2)的可解性还与信源有关,方程组(2)有惟一解的概率只有50%[4]。
第三,当卷积码的总约束长度较大时,识别过程非常耗时,因此无法在实际中应用。
因此,采用常规识别算,如何提高识别效率是重中之重。
3.2 基于校验矩阵的识别算法
卷积码序列G与校验矩阵H存在如下校验关系[5]

校验矩阵多项式的最高阶数根据实际应用设定为k,卷积码输出路数n,容易得到校验矩阵多项式系数的齐次线性方程组
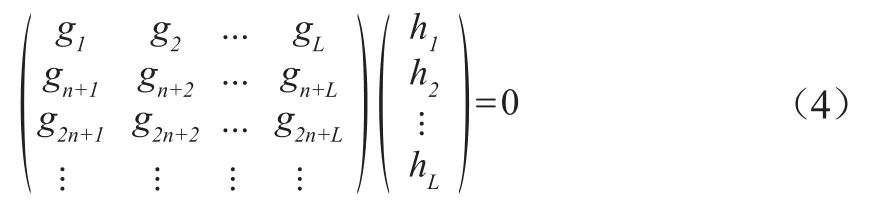
式中,gi为接收序列中第i位;L=n(k+1)。文献[6]针对式中的模型给出了相应的求解算法,将1/2码率卷积码校验矩阵的求解模型转化为关键模方程表示[7],求解该算法即转化为在集合φ(n)中寻找元素(h1(x),h2(x),k),使得k达到最小且(h1(0),h2(0))≠(0,0),φ(n)的定义如下
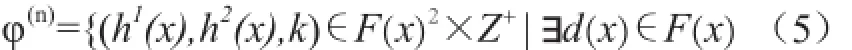
其中,F(x)为二元域上的多项式环。
3.3 基于欧几里德算法的识别算法
欧几里德算法又称辗转相除法[5],是一个迭代算法,可以用于计算两个多项式a(x)和b(x)的最大公约数d(x),然后找到一个表示a(x)和b(x)之间的线性联系,使其等于d(x),即找到方程

本方法即是应用欧几里得算法在有限域上的算法来求解卷积码生成多项式的。对于一个1/2码率的卷积码的识别,接收到的码字多项式是已知的c1(x)和c2(x),目标是寻找多项式g1(x)和g2(x),使得
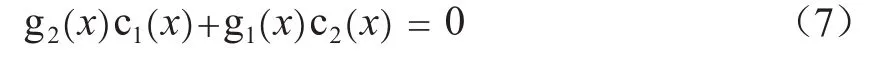
由于接收到的数据只是卷积码编码数据的一部分,并且,编码序列在传输过程中,也会遭受噪声的影响,使得c1(x)和c2(x)不一定满足式(7),所以需要对欧几里德算法进行修正,修正后的欧几里德算法过程如下:
第一步:参数初始化

第二步:对于i≥1,定义qi(x),ri(x)满足ri-2(x)= qi(x)ri-1(x)+ri(x),其中qi(x),ri(x)分别是ri-2(x)除以ri-1(x)所得到的商多项式和余数多项式。
第三步:迭代运算

第四步:终止条件

设此时i=n,可以得到g1(x)=g1,n(x),g2(x)= g2,n(x)。
4 算法性能比较
4.1 正确识别率比较
根据相关文献资料[8]可以得到前述三种算法在识别完全无误卷积码时的正确识别率,如表1所示。由表1可以看出,除了常规算法以外,另二种识别算法都能正确识别接收到的完全无误卷积码,正确识别率可以达到 。

表1 正确识别率比较结果
4.2 抗误码性比较
表2列出了3种算法的抗误码性能[4],从表中可以看出,除了常规算法以外,另外两种识别算法都具有一定的抗误码能力,基于校验矩阵的匹配识别算法抗误码能力与误码发生在截取码流中的位置有关;基于欧几里德算法的识别算法只能抗少量误码。

表2 抗误码性能比较结果
4.3 计算复杂度比较
常规识别算法的计算复杂度是O(N3)(其中N是接收码字长度)、基于校验矩阵的匹配识别算法的计算复杂度随着接收码字长度N的增加而增加,基于欧几里德算法最多需要L×N/2次多项式乘法和加法运算,其中L是生成多项式g1(x),g2(x)的最大阶次,即L=max(degg1(x),degg2(x));N是用于求解的码字序列长度,N≥3(L+1)。在接收码长N一定时,常规识别算法的计算复杂度最高,基于欧几里德算法的计算复杂度最低。
4.4 综合比较
综合上文对三种识别算法在识别1/2码率卷积码时的性能比较可以发现,常规识别算法无论在正确识别率、抗误码性能还是在计算复杂度上都不及其他算法;基于校验矩阵的匹配识别算法计算最简便,但抗误码性能不稳定,而基于欧几里德算法的识别算法正确识别率高、计算复杂度低,但是其抗误码性能有待改进。
5 总结与展望
随着通信对抗逐渐从信号对抗转向信息对抗,信道编码盲识别技术的地位越来越重要。本文简要介绍了现有三种卷积码信道编码的盲识别方法,分析了三种识别算法的算法性能。从分析中可以看到,现有信道编码识别技术尚存在许多局限和不足,需要进一步研究来补充和完善:在识别对象上,现有的研究主要集中在卷积码的研究,其他信道编码体制,如BCH码、RS码、Turbo码以及LDPC等的相关研究资料非常少;目前的卷积码识别方法也存在很多不足,普通卷积码的识别方法仅对1/2码率有效,不能适应高码率的情况,删除卷积码的识别方法不能快速稳定地完成识别,等等。■
参考文献
[1] 杜宇峰.信道编码分析识别技术研究[D].西安:电子科技大学,2012
[2] 刘健,谢锘,周希元.RS码的盲识别方法[J].电子科技大学学报,2009,38(3):363-368
[3] 解辉,王丰华,黄知涛.基于改进欧几里得算法的1/2码率卷积码盲识别方法[J].电子对抗,2010,1:32-36
[4] 宋镜业.信道编码识别技术研究[D].西安:西安电子科技大学,2009
[5] J H van Lint. Introduction to Coding Theory[M].Beijing:World Publishing Corporation,2003.
[6] 周亚建,刘健.(n,n-1,m)卷积码的盲识别[J].北京邮电大学学报,2010,33(3):135-138
[7] 邹艳,陆佩忠.关键方程的新推广[J].计算机学报,2006,29(5):711-718
Analysis of the Recognition Algorithm of Convolutional Code
Ding Qiao1, Xu Wei2
(1.PLA University of Science and Technology, Nanjing, 210007; 2.Air Force Communication Network Management Center, Beijing, 100843)
Abstract:Overview of the development of the recognition of channel coding technology is presented in this paper, the working principle of three convolutional code recognition algorithms, i.e.conventional recognition algorithm, parity check matrix-based recognition algorithm and Euclidean-based recognition algorithm is given, comparative analysis of three algorithms’-performance is presented in this paper.
Keywords:Convolutional encoding; Coding Recognition; Parity check matrix; Euclidean algorithm;Algorithm performance
doi:10.3969/J.ISSN.1672-7274.2016.06.004
中图分类号:TN97,TN92
文献标识码:A 文章编码:1672-7274(2016)06-0011-03
作者简介:丁 峤,解放军理工大学通信工程学院通信工程专业学生。
