基于有限域的LDPC卷积码构造算法
2016-10-24穆丽伟韩国军
穆丽伟, 韩国军, 方 毅
( 1.华南师范大学物理与电信工程学院, 广东省量子调控工程与材料重点实验室,广州 510006;2.广东工业大学信息工程学院,广州 510006;3.广东省广电检测仪器工程技术研究中心,广州 510006)
基于有限域的LDPC卷积码构造算法
穆丽伟1,3*, 韩国军2, 方毅2
( 1.华南师范大学物理与电信工程学院, 广东省量子调控工程与材料重点实验室,广州 510006;2.广东工业大学信息工程学院,广州 510006;3.广东省广电检测仪器工程技术研究中心,广州 510006)
采用有限域方法研究获得具有快速编码特性的规则、时不变LDPC(Low-Density Parity-Check,低密度奇偶校验)卷积码的构造算法. 首先给出基于有限域GF(q)所构造的准循环(QC)LDPC码的基矩阵结构特性;然后提供了一种新的代数构造及其对应的修正的矩阵结构;最后,根据QC与LDPC卷积码之间的环同构关系,获得了具有快速编码特性的LDPC卷积码的多项式矩阵结构. 代数构造方法简化了整个构造过程. 而LDPC卷积码的快速编码特性减小了编码复杂度,简化了编码器结构. 用基于置信传播(BP)的译码算法在加性高斯白噪声(AWGN)信道上获得的仿真结果表明,与其他结构化LDPC卷积码相比,文中所构造的码具有更好的性能.
LDPC卷积码; 代数构造; 有限域; 快速编码; BP算法
众所周知,与低密度奇偶校验(Low-Density Parity-Check,LDPC )分组码相比,LDPC卷积码有许多优势. 首先,它们可对输入比特流进行连续编译码;其次,在置信传播(Belief Propagation,BP)的译码算法下具有更好的性能;最后,其编译码器结构更简单. 自从1999年时不变LDPC卷积码[1]出现后,关于该码构造、编译码方法、编译码器的实现和性能分析等领域的研究,已经吸引了研究人员的注意. LDPC卷积码可分为2类:时变[2-4]和时不变码[5]. 由于时不变码可以简化构造过程以及编译码器结构,故本文致力于研究时不变LDPC卷积码的构造算法.
LDPC卷积码可用多项式矩阵表示. 当多项式矩阵中的每个矩阵元素为1个单项式时,LDPC卷积码有大环[6],此时,认为LDPC卷积码是好码. 由单项式构成的LDPC卷积码矩阵常由随机搜索算法获得. 该算法常被用于获得具有大环[6-8]或好的距离特性的码[9]. 代数构造算法[10-11]也常被用于构造LDPC卷积码,该算法还被用于构造单项式结构的LDPC卷积码.
本文采用代数方法获得了有限域GF(q)上具有快速编码特性的规则、时不变LDPC卷积码的单项式矩阵. 首先,给出构造LDPC卷积码基矩阵所需要的2个条件. 然后,给出具体的构造方法. 最后,通过修正该具体构造的算法,获得具有快速编码特性的LDPC卷积码. 与现有的具有单项式矩阵结构的其他LDPC卷积码[6,10]相比,本文所提出的LDPC卷积码在小的约束长度和错误平台下,具有良好的性能.
1 研究方法
描述时不变LDPC卷积码的多项式矩阵及其对应的二元矩阵结构,回顾基于有限域构造QC LDPC码的约束条件.
1.1时不变LDPC卷积码的矩阵结构
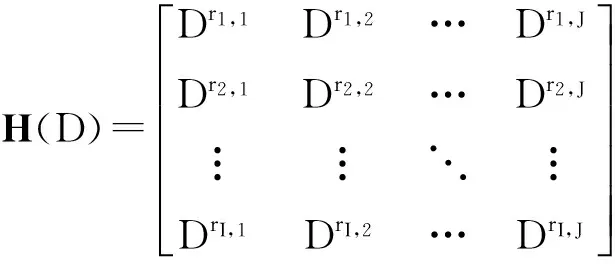
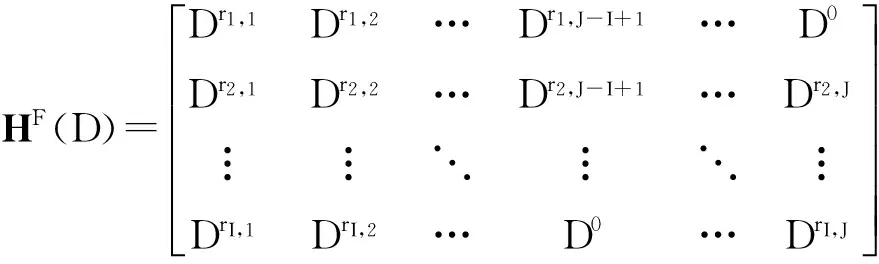
最大编码记忆ms,码率R=(J-I)/J的(ms,I,J)时不变LDPC卷积码的(I,J)多项式矩阵为:

(1)
该矩阵中每个输入元素是单项式,变量D为卷积码的延迟算子,D的幂ri,j(ri,j∈+,1≤i≤I,1≤j≤J)表示与序列中起始码元相比,1个码元延迟了多少时间单元. 该矩阵的最大编码记忆{ri,j},约束长度vs=(ms+1)J.
矩阵H(D)对应的半无限长二元奇偶校验矩阵如下:

(2)
其中,Hi(i=0,1,…,ms)是I×J二元子矩阵,即:

该二元矩阵H是规则矩阵,每列有I个1,从第(ms·I+1)行开始,每行有J个1.
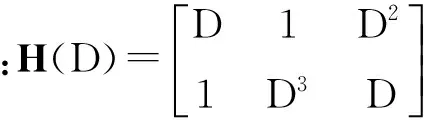
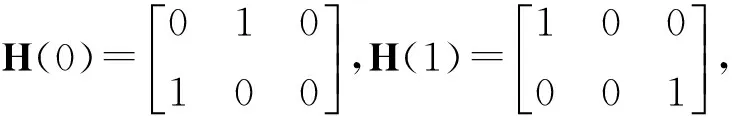
.
图1画出了LDPC卷积码多项式矩阵与二元矩阵之间的关系. 只要多项式矩阵H(D)中D的幂满足rj,n- ri,n=rj,m- ri,m,H(D)对应的二元矩阵H则会有4环.
1.2QC LDPC码基矩阵与LDPC卷积码
考虑有限域GF(q),q是素数的幂. 假设α为有限域GF(q)上的基本元. 令α≡0,α0=1,α,…,αq-2代表 GF(q)上所有元素且αq-1=1. 众所周知,基于有限域乘群构造的QC LDPC的基矩阵:

(3)
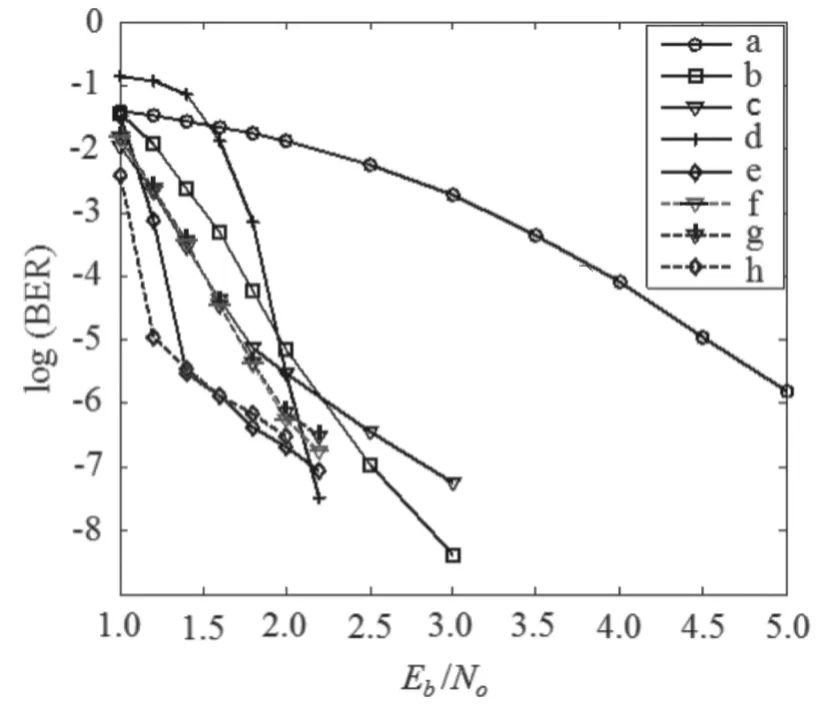
该矩阵必须满足α-乘行约束条件[12]:(1)αkwi和αlwi至少在J-1位置不同,0 图1 多项式矩阵H(D) 根据QC和卷积LDPC码之间的环同构关系,LDPC卷积码的多项式矩阵H(D)可由QCLDPC码获得,并且它的二元矩阵的最小环长取对应的QCLDPC最小环下届[10]. 根据前文所述,可推断出基于有限域所构造的基矩阵W满足如下2个特性:(1)基矩阵W的每个矢量wi中至多只有1个0元素;(2)基矩阵W的任意2个矢量wi和wj至少有J-1个位置不同,并且rj,n-ri,n≠rj,m-ri,m,i≠j,n≠m. 根据上述2个推断性质,本文提出一种新的代数方法用以构造基于有限域GF(q)的(I,J)基矩阵W,具体表示如下: (4) 其中,每个元素αri,j=αJ-I·αi·αj+αq-2,乘和加执行模q运算. 该基矩阵W中每行或每列元素各不相同,元素差值rj,n-ri,n=αJ-I·αn·αj-i,rj,m-ri,m=αJ-I·αm·αj-i. 显然,rj,n-ri,n≠rj,m-ri,m. 由此可知,基矩阵W满足α-乘行约束条件. 用延迟算子D代替基矩阵中的α[13],可获得规则、时不变LDPC卷积码的多项式矩阵形式 (5) (6) 以确保其具有快速编码特性. 在AWGN(Additive White Gaussian Noise)信道上,用基于置信传播(Belief Propagation, BP)的译码算法进行仿真,给出矩阵HF(D)所对应的具有快速编码特性的LDPC卷积码的仿真结果. 最大译码迭代次数为50. 除了最小环长为(59,2,6)的LDPC卷积码,其他被仿真码的最小环长均为6. 图2给出了基于不同有限域构造的不同码率的LDPC卷积码的译码性能,图中虚线数据来自文献[6]108和[10]2978-2981. 对于(54,4,6)码,最大编码记忆ms=50,行重I=4,列重J=6,约束长度vs=(ms+1)·J=306,在Eb/N0=2.2dB时,误码率(BER) 约3×10-7,并且没有误码平台. 本文中,Eb是传输每比特位信息所需要的平均能量,N0是AWGN信道上的单边功率谱密度. 然而,由搜索算法获得的约束长度vs=290的(57,3,5)LDPC卷积码[6]108,在E0/N0=2.2dB时,BER约为1.4×10-6. 而由代数方法构造的约束长度vs=295的(58,3,5)LDPC卷积码[10]2978,在E0/N0=2.2dB时,BER约为2.2×10-6. 显然,在相似的约束条件下,本文的(50,3,5)LDPC卷积码比文献[6]和[10]的(57,3,5)码和(58,3,5)码更好. 由图2也可看出,约束长度为vs=1 440,码率R=3/6的(239,3,6)LDPC卷积码优于文献[10]2981构造的约束长度为vs=1 950、码率R=2/5的(389,3,5)LDPC卷积码. a:(59,2,6)码, vs=360 ,GF(26);b: (40,3,6)码, vs=246,GF(26);c: (44,3,5)码, vs=225,GF(26);d: (50,4,6)码, vs=306,GF(26);e: (239,3,6)码, vs=1 440,GF(35);f: (57,3,5)码, vs=290,GF(61)[6];g: (58,3,5)码, vs=295,GF(61)[10];h: (389,3,5)码, vs=1 950,GF(421)[10]. 图2AWGN信道上基于不同有限域构造的不同码率的LDPC卷积码性能 Figure2PerformanceofproposedLDPCconvolutionalwithdifferentratesanddifferentfinitefieldsoverAWGNchannels 图3给出了不同有限域GF(q)上,(I,J)=(3,6)的LDPC卷积码性能. 本文提出的(160,3,6)LDPC卷积码,在Eb/N0>2dB时, 比文献[10]2981的Fig.12中所构造的(187,3,5)码性能要好,在Eb/N0>1.5dB时,比文献[6]108的Fig.9所构造的(204,3,5)码性能要好. 由性能比较结果可知,在高信噪比区,与其他具有类似结构的码相比,本文所提出的LDPC卷积码在小约束长度下具有好的译码性能,并且误码平台较低. 更值得一提的是,本文所提出的码具有快速编码特性可节省硬件资源[14]. a:(47,3,6)码, vs=288,GF(72);b:(110,3,6)码, vs=666,GF(112);c:(120,3,6)码, vs=726,GF(53);d:(160,3,6)码, vs=966,GF(132);e:(204,3,5)码, vs=1 025,GF(241)[6];f:(187,3,5)码, vs=940,GF(211)[10]. 图3AWGN信道上基于不同有限域构造的码率R=0.5的LDPC卷积码性能 Figure3PerformanceofLDPCconvolutionalcodeswithrate0.5overdifferentfinitefieldsGF(q)overAWGNchannels 本文提出了一种新的具有快速编码特性的规则和时不变LDPC卷积码. 根据有限域乘群构造QC LDPC码所需要的2个α-乘约束条件,以及QC与卷积LDPC码之间的环同构关系,给出了构造结构化LDPC卷积码基矩阵的条件,并提出了1种代数构造方法. 对所获得的多项式矩阵进行修正后,最终生成具有快速编码特性的LDPC卷积码单项式矩阵. 仿真结果表明,本文提出的LDPC卷积码在小记忆和小约束长度下有很好的译码性能和较低的误码平台. 显然,该特性可节省硬件资源. 而且,与时变LDPC卷积码相比,该码的时不变特性和快速编码特性减小了编码复杂度. 另外,与搜索算法构造时不变LDPC卷积码的构造过程相比,本文提出的方法更简单. [1]FELTSTROM A J, ZIGANGIROV K S. Time-varying periodic convolutional codes with Low-Density Parity-Check Matrix[J]. IEEE Transactions on Information Theory, 1999, 45(6): 2181-2191. [2]GROSJEAN L, RASMUSSEN L K, THOBABEN R, et al. Systematic LDPC convolutional codes: asymptotic and Finite-Length anytime properties[J]. IEEE Transactions on Communications, 2014, 62 (12): 4165-4183. [3]LENTMAIER M, MITCHELL D G M, FETTWEIS G P,et al. Asymptotically good LDPC convolutional codes with AWGN channel thresholds close to the Shannon Limit[C]∥International Symposium on Turbo Codes and Iterative Information Processing(ISTC). Brest:[s.n.], 2010: 324-328. [4]KUDEKAR S, RICHARDSON T, URBANKE R L. Spatially coupled ensembles universally achieve capacity under belief propagation[J]. IEEE Transactions on Information Theory, 2013, 59 (12): 7761-7813. [5]BALDI M, CANCELLIERI G, CHIARALUCE F. Array convolutional Low-Density Parity-Check codes[J]. IEEE Communicaions Letters, 2014, 18(2): 336-339. [6]ZHOU H, GOERTZ N. Girth analysis of Polynomial-Based Time-Invariant LDPC convolutional codes[C]∥ International Conference on Systems, Signals and Image Processing (IWSSIP). Vienna: IEEE, 2012: 104-108. [7]ROY E, CARDINAL C, HACCOUN D. Recursive convolutional codes for Time-Invariant LDPC convolutional codes[C]∥IEEE International Symposium on Information Theory Proceedings (ISIT). Texas: IEEE, 2010: 834-838. [8]CARDINAL C, HE Y, HACCOUN D. A new approach for the construction of powerful LDPC convolutional codes[C]∥IEEE Vehicular Technology Conference (VTC). Singapore: IEEE, 2008: 1176-1180. [9]CHEN T H, CHEN K, LIN M C. A construction of LDPC convolutional codes with close distance bounds[C]∥IEEE International Symposium on Information Theory and its Applications (ISITA). Victoria: IEEE, 2014: 90-94. [10]TANNER R M, SRIDHARA D, SRIDHARAN A, et al. LDPC block and convolutional codes based on circulant matrices[J]. IEEE Transactions on Information Theory, 2004, 50 (12): 2966-2984. [11]PUSANE A E, SMARANDACHE R, VONTOBEL P O, et al. Deriving good LDPC convolutional codes from LDPC block codes[J]. IEEE Transactions on Information Theory, 2011, 57(2): 835-857. [12]LAN L, ZENG L Q, TAI Y Y, et al. Construction of Quasi-Cyclic LDPC codes for AWGN and binary erasure channels: a finite field approach[J]. IEEE Transactions on Information Theory, 2007, 53 (7): 2431. [13]MU L W, LIU X C, LIANG C L. Construction of LDPC convolutional codes over finite fields[J]. IEEE Communications Letters, 2012, 16(6): 898. [14]ZHAO Y,LAU F. Implementation of decoders for LDPC block codes and LDPC convolutional codes based on GPUs[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 25(3): 663-672. 【中文责编:成文英文责编:李海航】 Construction of LDPC Convolutional Codes Based on Finite Fields MU Liwei1,3*,HAN Guojun2,FANG Yi2 (1.Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Physics and Telecommunication Engineering,South China Normal University, Guangzhou 510006, China; 2. School of Information Engineering, Guangdong University of Technology,Guangzhou 510006, China; 3. Guangdong Provincial Engineering Research Center for Optoelectronic Instrument, Guangzhou 510006, China) A new algebraic construction of regular, time-invariant low-density parity-check (LDPC) convolutional codes with fast encoding based on finite fields is proposed in this paper. It is first specified the structure properties of a base matrix which is associated with a quasi-cyclic (QC) LDPC code constructed based on finite fields GF(q). A concrete algebraic construction and its modified form of the matrix are then given. Finally, according to the ring isomorphism relationship between a QC code and a convolutional LDPC code, the polynomial matrix corresponding to an LDPC convolutional code with fast encoding is developed. The algebraic construction simplifies the construction process significantly. In particular, the fast encoding property can both reduce the encoding complexity and simplify encoder structure. Simulation results show that the proposed LDPC convolutional codes have more excellent performance in comparison with the existing counterparts under belief propagation (BP) decoding algorithm over additive Gaussian white noise (AWGN) channels. LDPC convolutional codes; algebraic construction; finite fields; fast encoding; BP algorithm 2016-02-27 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(61401164,61501126,61471175);广东省自然科学基金项目(2014A030310308) 穆丽伟,讲师,Email:liweimuscnu@163.com. TN911.22 A 1000-5463(2016)04-0016-05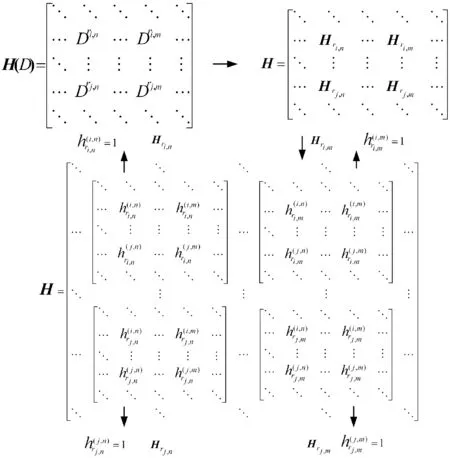
2 具有快速编码特性的LDPC卷积码

3 结果与讨论

4 结论
