大约束长度卷积码编码器的改进与实现*
2018-07-26张涛涛王满喜杨志飞
张涛涛,王满喜,荣 辉,杨志飞
(1.电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003;2.中国洛阳电子装备试验中心,河南 洛阳 471003)
0 引 言
对于卷积码而言,并没有可用的代数结构构造好的卷积码编码器。考虑到生成多项式为G(X)=1+X+X2+X4+X8+X10的(15,5)BCH 码 的 最小距离dg=7,对偶码的生成多项式是h(X)=(X15-1)/g(X)=X5+X3+X+1且dg=4。符合生成多项式g(D)=1+D+D2+D4+D5+D8+D10且码率为R=1/2的卷积码有dfree≥min(7,8)。生成矩阵为 G(D)=[1+D+D2+D4+D51+D2]。可以看出,该编码器的最小自由距离为dfree=7,约束长度为5。类似的构造可以产生码率为1/2的卷积码,然而构造这类卷积码有两个困难。第一个难题是寻找具有最大自由距离的大约束长度的卷积码,第二个难题是此限与循环码的最小距离有关。该难题已由Juestesen解决[1]。Jusetesen的构造限dfree≥dg,但它涉及到关于g(X )根的条件相当复杂,且在二进制情况下,仅仅可用来构造奇数n值的卷积码。Tanner的构造得到限dfree≥dmin,其中dmin是相联系的循环码的最小距离[2]。
一般构造大约束长度的卷积码要考虑编码器的性能。卷积码编码器的纠错能力与自由距离之间存在紧密联系。具体来讲,编码器的性能与卷积码的自由距离之间存在正相关关系。也就是说,编码器的性能会随自由距离的增加而得到改善。因此,要改善编码器的性能,就要从卷积码的自由距离入手,通过分析对比大约束长度卷积码编码器的自由距离,达到寻找好的大约束长度卷积码编码器的目的。一旦卷积码的码率确定了,就可以把卷积码的自由距离和距离谱作为寻找好的卷积码编码器的指导。维特比译码和序列译码的性能主要受卷积码的列距离特性的影响[3]。对于序列译码,卷积码的列距离dl应该随着l增加,至少是非减少的[4-6],由此得到具有良好距离特性的卷积码。
1 已有的搜索算法
大多数情况下,搜索大约束长度卷积码的工作量随着卷积码约束长度的增加而迅速增加。利用计算机搜索好的大约束长度的卷积码是非常耗时的运算,因此计算机搜索只能被限定在较短的约束长度。但是,即便对于小的约束长度,穷搜索的方法也是不可行的[7-8]。因此,需要提出新的筛选规则寻找好的卷积码。Bahl、Cullum、Frazer和Jelinek提出了一种的基于维特比算法寻找dfree和Adfree的计算机搜索方法[9],并由Larsen修改[10]该算法,假设接收到的序列全是零,把在栅格中的搜索限制在以一个非零信息分组开始的路径,采用0量度代表一致,+1代表不一致,搜索具有最小量度的路径。一旦在零状态的幸存路径的量度低于或等于其他所有路径,算法就可以停止。所以,在全零状态下的量度就等于dfree,这是因为没有一条其他幸存的路径能以更小的量度汇合到全零状态。对于恶性编码器,由于状态图中的零环路,在全零状态下的幸存路径可能无法达到最小的量度。该算法能够计算约束长度为20的卷积码的dfree和最小自由距离为dfree的个数Adfree。对于更大的约束长度,算法要存储的空间数随着约束长度的增加呈指数倍数增加而无法满足,因此必须尝试其他方法来寻找dfree。
2 改进的搜索算法
对于较大的约束长度,目前还没有通用的计算dfree的方法。传统的利用计算机搜索大约束长度的卷积码的算法在文献[11-12]中已有介绍,能做到的最大约束长度不超过30。为了能够找到约束长度在30以上的卷积码,需找到一种新的方法寻找更大约束长度的卷积码。
单次寻找大约束长度最优卷积码的算法流程如图1所示。

图1 计算机搜索卷积码的堆栈算法流程
通过对卷积码自身特性和堆栈算法的研究,提出了快速寻找有限数量好的大约束长度的卷积码方法。
(1)随机设计首位和末位分别为1,生成多项式重量不同时为偶的编码器。
(2)检验(1)中设计的编码器的距离分布特性。
(3)验证(1)中设计的编码器的自由距离是否符合预估的上限和下限。
对于码树图中的节点,需要设置一个结构体。该结构体中应该包含有分裂到该节点的状态、该节点的码重、当前节点的量度和当前的状态到全零状态所需的最少分裂次数。算法开始时,放置一个初始状态为1,码重为2,当前的状态到全零状态所需的最少分裂次数为编码器的约束长度,节点的量度为码重和当前状态到全零状态所需最少分裂次数的和。对栈顶的节点进行分裂,每次分裂都是分别进行0和1的分裂。如果分裂后的节点的码重满足设定的上限,则把该节点存储在堆栈,把堆栈的顶节点覆盖,并根据每个节点的量度进行完全排序,使较快回到全零状态的节点排在栈顶,为下一次的分裂做好准备。排序的目的主要是为了分裂较快回到全零状态的节点。如果当前的节点到达树的终点且节点的码重未超过设定的上限,则存储该节点至另一块内存空间。如果存储的节点状态点到达了全零且码重不大于设定上限、节点的数目小于设定的存储数目,总的计算量小于Clim,则继续分裂节点;否则,输出存储的节点。
该算法能够停下来的二个条件:
(1)存储满足条件的节点等于设定的数目;
(2)总的计算量超过了Clim。
一旦该算法满足上述结束条件,该算法就停止。只要是一个堆栈,堆栈的容量是确定的,就有可能出现堆栈满的情况。考虑到存放在堆栈底部的节点被选择作为最优路径上的节点的可能性非常小,通常在堆栈满的情况下,用堆栈顶部的进行0分裂的节点覆盖当前的栈顶节点,而进行1分裂后的节点覆盖堆栈底部的节点。因此,该堆栈成为首尾相连的循环堆栈。每进行一次分裂都要进行排序。为了方便排序和堆栈的栈顶指向,需要设置一个堆栈指针始终指向栈顶。由于排序需要耗费大量的时间,堆栈的长度不易较大。为了使码树能够充分分裂,堆栈的长度也不易过小。综合以上两方面考虑,堆栈的大小应该根据卷积码的约束长度取一个较为合适的值。利用该搜索算法找到的部分具有较大约束长度的卷积码如表1所示,其中生成多项式使用十六进制表示。
3 仿真测试
卷积码的性能必须通过加噪声的信道进行检验,以检验编码器在不同信道比条件下的误码率。采用费诺译码算法在受扰信道中检验,以测定大约束长度卷积码在噪声干扰情况下对误码率的改善情况。图2给出了约束长度为60和32的大约束长度卷积码在不同信噪比下出现错误帧的概率。可以看出,当约束长度固定时,随着信噪比的增加,错误帧的概率降低;当信噪比固定时,随着约束长度的增加,错误帧的概率明显得到改善。
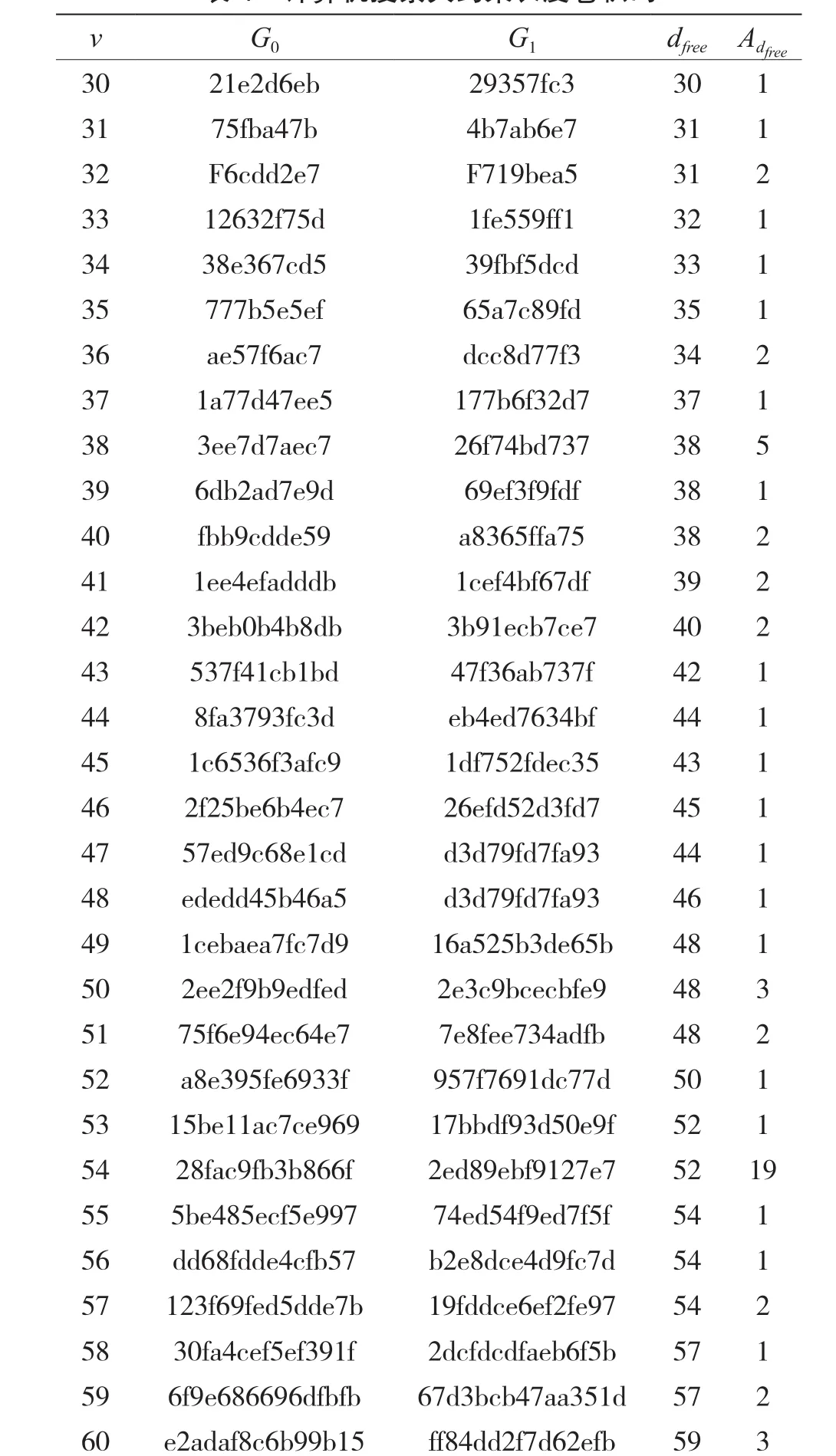
表1 计算机搜索大约束长度卷积码

图2 不同信噪比下不同约束长度卷积码性能对比
4 结 语
本文提出了一种改进的大约束长度卷积码搜索算法,利用该搜索算法可以找到约束长度大于30的卷积码编码器。利用费诺译码算法对不同约束长度的卷积码编码器的性能进行检验,结果表明,通过该搜索算法找到的大约束长度卷积码的在同等信噪比的情况下的误码率较低。
