(n,1,L)卷积码的逻辑运算译码方法
2018-11-19杨雪梅毕春艳
杨雪梅,毕春艳
(四川大学锦江学院 电气与电子信息工程学院,四川 眉山 620860)
0 引 言
卷积码是1955年由Elias等人提出的。在设备复杂度相同的条件下,它的性能优于分组码,纠错能力随约束长度的增加而增强[1-2]。目前,卷积码最实用的(n,k,L)卷积码是k=1的(n,1,L)卷积码[3],已广泛应用于实际通信系统中,如2G、3G和商业卫星通信系统等。例如,为了实现前向差错控制,GSM移动通信系统在下行和上行链路中都采用了(2,1,5)卷积码,IS-95 CDMA系统在下行链路中采用(2,1,9)卷积码,而上行链路中采用(3,1,9)卷积码。
常用的卷积码译码方法还有Viterbi译码[4]。但是,随着约束长度的增大,它的算法和硬件实现复杂度也会增加。此外,还有序列译码[5]和门限译码[6],但性能都较Viterbi译码差。文献[7]提出了一种逻辑代数译码算法,但需要将错误类型分类讨论。本文为(n,k,L)卷积码设计了一种基于逻辑运算的译码方法,原理简单,适合于所有(n,1,L)卷积码的译码。
1 卷积码的编译码原理
1.1 编码原理
一个(n,k,L)卷积编码器由 L·k-1级移位寄存器和n个模2和加法器(异或门)构成的输出发生器组成[3]。每输入k比特,编码输出一个n比特码字,如图1所示。
一个典型的(2,1,3)卷积码的原理图如图2所示,连接矢量为G1=(111)2和G2=(101)2。
(2,1,3)卷积码的两个异或门的编码输出逻辑表示式为:
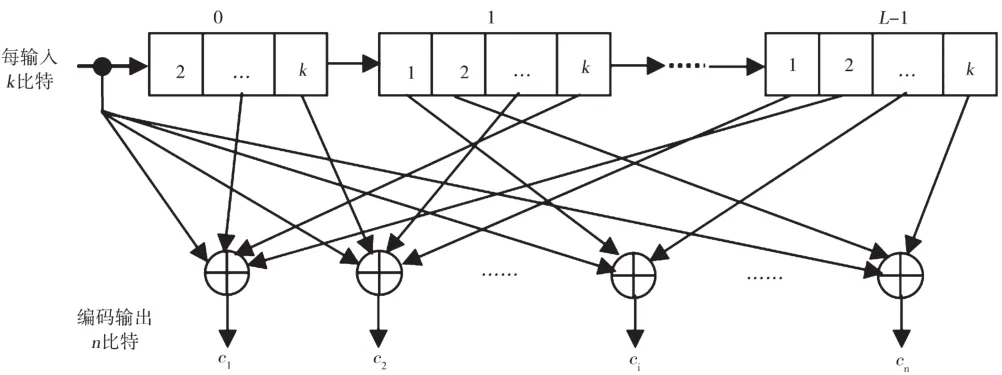
图1 (n,k,L)卷积码编码器

图2 (2,1,3)卷积码编码器
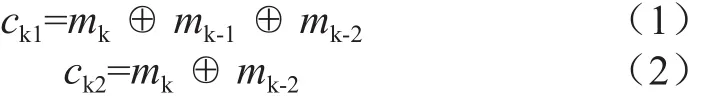
可见,输入1位数字信号,可以得到2位卷积码输出数据。
(3,1,9)卷积码连接矢量和异或门的编码输出逻辑表示式为:可见,输入1位数字信号,可以得到3位卷积码输出数据。

1.2 基于逻辑运算的译码原理
卷积码译码过程中,不仅要从现在时刻收到的码组中提取译码信息,而且要从以前或以后的多个时刻(与约束长度有关)收到的码组中提取有关信息并纠错。
目前,卷积码译码方法有很多,可以分为两大类:一类是是门限译码[5],另一类是基于最大似然原理的译码,包括Viterbi译码[4]和序列译码[6]。
逻辑运算的算法原理主要是根据异或运算的因果互换关系进行编码逆运算从而实现译码,属于最大似然译码。
以(2,1,3)卷积码为例,它的译码器结构如图3所示。

图3 (2,1,3)卷积码的译码器
利用异或运算的可逆性,由编码方程式可得计算重建信息码元mk的译码方程:
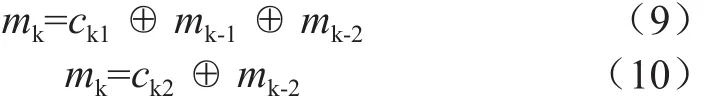
可见,异或逆运算后有2个mk。若2个mk相同,则译码正确;若不同,表明接收到的子码ck有错,或前面某一次译码中mk-n可能出现误码。此时,需检查可能情况进行纠错和判决,排除错误,最终确定输出译码值。其中,纠错和判决的思想采用择优保留的原则。因此,译码器中异或门的输出最终会进入最大似然译码算法进行判决,实现最终的译码。
同理,(n,k,L)卷积码有n个码采用逻辑运算译码后会得到n个mk。若n个mk相同,则译码正确;若不同,根据最大似然思想进行判决,实现译码。在随机错误干扰下,发送的编码信号不容易成片出现。n越多,越有利于使用最大似然算法进行译码,译码纠错越容易,出现误码的几率相对减小。
例如,在(3,1,9)卷积码中,在进行逻辑运算译码后得到3个mk,根据最大似然思想,有:
(1)若有3个mk相同,则判决该mk为译码值;
(2)若3个mk不相同,此时可能出现错误。为了避免误码,需假设不相等位置的mk情况继续译码,选择误码最优的结果;
若在接收子码ck中有连续2个以上错误,则译码可能出现误码,但后续译码也可进一步发现误码,此时需要通过相关算法进行纠正。
2 实现与仿真
通过卷积码编码方程,利用matlab仿真平台得到其发送子码。若发送信号序列为110100111,如表1所示。

表1 编码举例
在matlab仿真平台上,对几种常用的卷积码如(2,1,5)、(3,1,9)等基于逻辑运算译码进行仿真,并通过高斯白噪声信道随机加错,检查其误码特性。译码流程图如图4所示。
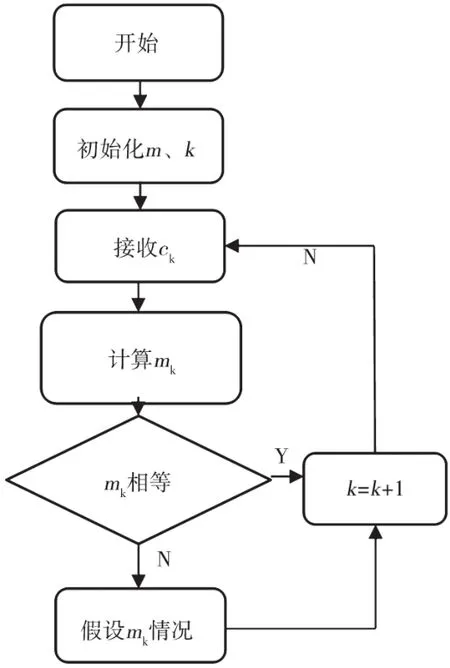
图4 (n,1,L)卷积码逻辑运算译码流程
随机产生一串二进制数字序列,测试长度为1 000,在不同信噪比SNR下,(2,1,5)和(3,1,9)卷积码的误码率如表2所示。
由表2可知,(2,1,5)和(3,1,9)卷积码均能在逻辑运算译码方法下实现译码。约束长度不同,检错纠错能力也有所不同。但是,算法或程序尚存在不成熟之处,需进一步研究改进性能。

表2 SNR与误码率对照表
3 结 论
利用逻辑异或运算的可逆性,将接收子码与移位寄存器中数据根据编码规则进行异或逆运算,得到n个发送数据,并根据最大似然思想完成对(n,k,L)卷积码的逻辑运算译码功能,并通过matlab仿真验证了其功能。该算法简单,容易实现,对(n,k,L)卷积码n>2时均适用。
