构造辅助圆巧解一类与弦有关的垂直问题

李　波

(四川省苍溪中学校，628400)

构造辅助圆巧解一类与弦有关的垂直问题

李波

(四川省苍溪中学校，628400)

随着课改的推进,对直线和圆的考查,主要以直线和圆的位置关系为主,题目难度适中,既着重对基础知识的考查、更注重对基本技能的考查．求解直线与圆相交的问题，常用方法有几何法与代入消元法,两者相辅相成,相互统一;针对与相交弦有关的垂直问题,笔者巧妙地构造了辅助圆,将直线与圆的问题转化为圆与圆的问题使问题的解答得以简化.下面看具体的几个例子．

一、建立等式,求参数

例1已知圆C:x2+y2+x-6y+m=0

和直线l:x+2y-3=0交于P,Q两点,且OP⊥OQ(O为坐标原点),求圆C的圆心坐标与m的值

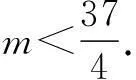
如图1,设以PQ为直径的圆的方程为C1:x2+y2+Dx+Ey+F=0,由OP⊥OQ知,点O在圆C1上,所以F=0.由联立方程组

得(D-1)x+(E+6)y-m=0,即圆C与圆C1的交线PQ为

(D-1)x+(E+6)y-m=0.

又P,Q在直线x+2y-3=0上,所以

评注圆的一般方程里含有参数,一定要记得考虑D2+E2-4F>0,最终算出来的参数,一定要代回去检验．在圆中,与弦有关的垂直问题,必有一个直角三角形,可以考虑以斜边为圆的直径构造辅助圆,这样就可以将问题转化为圆与圆相交的问题．

上述试题是本校的一道月考题,在2000份试卷中,几乎所有的考生都使用代数法,将题中的垂直问题转化为两根之和与两根之积的代数问题,但有一个考生利用题中的垂直关系,巧妙地构造辅助圆来解决．

二、以形助解,求最值

例2已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0)B(m,0)(m>0).若圆C上存在点P,使得∠APB=90°,则m的最大值为 ()

(A)7(B)6(C)5(D)4

解如图2,设以AB为直径圆的方程为x2+y2=m2.由∠APB=90°知,圆x2+y2=m2与C:(x-3)2+(y-4)2=1相交．由

得6x+8y-m2-24=0,

易知,当直线6x+8y-m2-24=0与圆C:(x-3)2+(y-4)2=1相切时,m有最小值和最大值,所以圆心C(3，4)到直线6x+8y-m2-24=0的距离

解得m2=16或m2=36.因为m>0,所以m=4或6,显然m的最大值为6．

评注由圆的性质知,直径所对的圆周角为直角,因此垂直问题可以考虑构造辅助圆.又因为点的存在问题即为图象相交,因此本题将问题转化为已知圆心,在圆与圆相交的条件下,求半径最值的问题,借助图象,数形结合便可快速求得半径的最大值,最小值．

三、合情推理,化切为弦

例3如图3，已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点.

(2)求证:直线AB恒过定点.

解(1)如图3,由QA,QB分别切⊙M于A,B两点,知MA⊥QA,MB⊥QB,由此可得,以MQ为直径的圆必过A、B两点,又,A、B两点在⊙M上,所以直线AB为两圆的交线．

设Q点的坐标为(t,0),则MQ为直径的圆的方程为

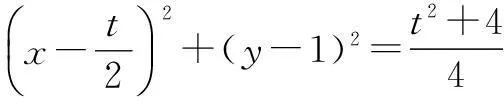
整理得x2+y2-tx-2y=0.

得交线AB的方程为tx-2y+3=0,所以圆心M到直线AB的距离为

评注过圆外一点作圆的切线，必有两条切线.利用切线与半径的垂直关系,可以考虑构造辅助圆,运用圆与圆相交的知识,求出两切点所在的直线方程．

四、寻找关系,求轨迹

例4如图4所示,已知P(4,0)是圆x2+y2=36内的一点,A,B是圆上两动点,且满足∠APB=90°, 求矩形APBQ的顶点Q的轨迹方程．

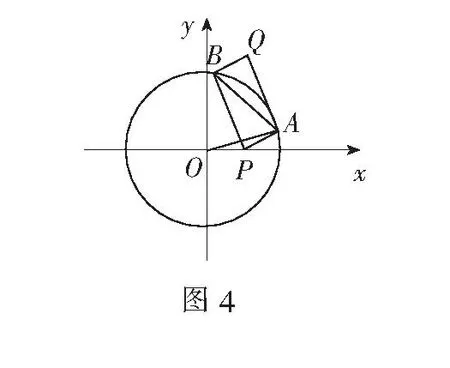
解设点Q的坐标为(x0,y0),P(4,0)，则以PQ为直径的圆的方程为(x-x0)(x-4)+(y-y0)y=0，整理得x2+y2-(4+x0)x-y0y+4x0=0.由联立方程组

得AB的方程(4+x0)x+y0y-36-4x0=0.

因为PQ的中点在交线AB上，所以

例5已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点．

(1)求线段AP中点的轨迹方程;

(2)若∠PBQ=90°,求线段PQ中点的轨迹方程．

解(1)略.

评注根据题中垂直条件,可以考虑辅助圆,在利用圆与圆相交的知识得到交线方程．同时需要考虑圆过定点,圆心在交线上,即可求出轨迹问题．

解题是数学永恒的主题,数学的解题历程是一项富有挑战性的活动,每一次的解题思维过程都会给我们留下深刻的解题体验和感悟.新课标明确提出了使学生获得数学的基本知识、基本技能、基本思想、基本活动经验的目标要求.对于一个数学问题,需要我们发散思维,善于联系,多角度深入思考,可以得到不同的解法,从而训练思维的灵活性,优化思维品质.