例说一类递推数列问题的求解方法

黄建荣

(江苏省泰兴市第四高级中学，225411)

例说一类递推数列问题的求解方法

黄建荣

(江苏省泰兴市第四高级中学，225411)

在数学竞赛或高考中，经常会出现形如an+1=λan+kqn+c的数列问题.这种题型结构复杂，变化较多，学生往往思维堵塞，难以理清头绪，找不到解题的切入点.解决这类题目主要思想方法是化归思想，即将其转化为常见的等差或等比数列，但是由于其错综复杂，使得转化比较困难.现通过例题对它的三种特殊类型进行解析.

一、形如an+1=λan+kqn(c=0,λ≠q)

例1已知数列{an}各项均为正，a1=2,an+1=2an+3·5n,求数列{an}的通项公式.

分析本题的解法是利用待定系数法，构造一个新的等比数列.

解设an+1+k·5n+1=2(an+k·5n),

则an+1=2an+2k·5n-k·5n+1

=2an+(2k-5k)·5n

=2an-3k·5n,

比较系数得k=-1.

∴an+1-5n+1=2(an-5n)(n≥1),

∴an-5n是以a1-5=-3为首项，2为公比的等比数列，

∴an-5n=-3×2n-1,

∴an=5n-3×2n-1.

评注本题在求解中注意到λ≠q这个因素，通过待定系数法构造了一个新的等比数列.要注意的是在用待定系数法设定的等式中左边5的幂指数是n+1,右边5的幂指数是n,与相应项的下标一致，2是原递推关系中an的系数λ.

例2已知数列{an}前n项和为Sn满足：2Sn=an+1-2n+1+1,且a1,a2+5,a3成等差数列，求数列{an}的通项公式.

解在2Sn=an+1-2n+1+1中，令n=1,得2S1=a2-22+1,即a2=2a1+3.

令n=2，得2S2=a3-23+1,即a3=6a1+13.

∵a1,a2+5,a3成等差数列，

∴2(a2+5)=a1+a3,

∴4a1+16=a1+6a1+13,

∴a1=1,a2=5.

∵2Sn=an+1-2n+1+1,

∴2Sn+1=an+2-2n+2+1.

两式相减，得2an+1=an+2-an+1-2n+1,

∴an+2=3an+1+2n+1.

(*)

设an+2+k·2n+2=3(an+1+k·2n+1),则

an+2=3an+1+k·2n+1,

与(* )比较得k=1，

∴an+2+2n+2=3(an+1+2n+1)(n≥1).

又a2+22=9,a1+21=3,

∴a2+22=3(a1+21),

∴a2+2n是以a1+21=3为首项，3为公比的等比数列，

∴an+2n=3×3n-1=3n,

∴an=3n-2n.

二、形如an+1=λan+kqn(c=0,λ=q)

例3已知数列{an}各项均为正，a1=2,an=2an-1+2n+1(n∈N*,n≥2),求数列{an}的通项公式.

分析在本题的递推关系中，λ=q,解题时可以在等式两边同除以qn,构造一个新的等差数列.

解∵an=2an-1+2n+1,

等式同边同时除以2n,得

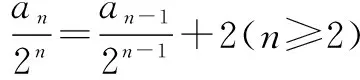
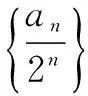
∴an=(2n-1)·2n.

评注注意本题中λ=q，等式两边同时除以qn(有时也可以是qn-1,qn+1)，譬如这一题也可以这样解：

∵an=2an-1+2n+1,

等号两边同时除以2n+1,得

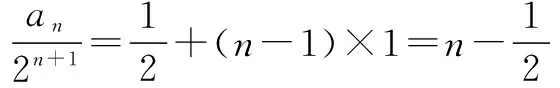
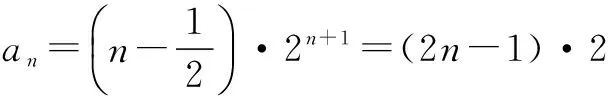
例4已知数列{an}中，前n项和为Sn,且Sn+1=4an+2,n∈N*,a1=1.

(1)设数列{bn}满足bn=an+1-2an,求证{bn}是等比数列；

(2)求数列{bn}的通项an.

解(1)∵Sn+1=4an+2,

∴Sn+2=4an+1+2.

两式相减，得

Sn+2-Sn+1=4an+1-4an,

即an+2=4an+1-4an,

∴an+2-2an+1=2(an+1-2an)(n≥1),

即bn+1=2bn.

∵S2=4a1+2,∴1+a2=4+2,

∴a2=5,

∴b1=a2-2a1=3,

∴{bn}是等比数列.

(2){bn}是以3为首项，2为公比的等比数列，

∴bn=3×2n-1,∴an+1-2an=3×2n-1,

∴an+1=2an+3×2n-1.

等式两边同时除以2n+1,得

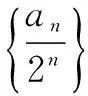
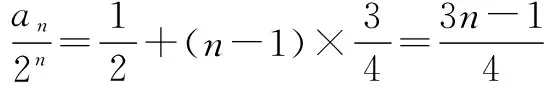
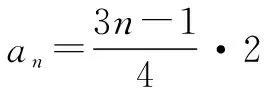
三、形如an+1=λan+kqn+c(c≠0,λ=q)

例5数列{an}满足an+1=2an+2n-1(n∈N*),a1=2,求数列{an}的通项an.

分析注意本题中c≠0,λ=q，先将常数-1放入数列中，构成一个新的递推公式，得到形如bn+1=λbn+qn(λ=q)的递推关系；再根据λ=q情形的处理方法，两边同除以qn+1，构造一个等差数列.

解由an+1=2an+2n-1,设

an+1+m=2(an+m)+2n,

则an+1=2an+2n+m，

与原递推关系比较，得m=-1，

∴an+1-1=2(an-1)+2n(n≥1).

等式两边同时除以2n+1,得

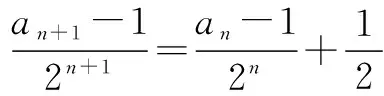
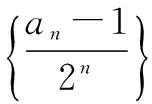
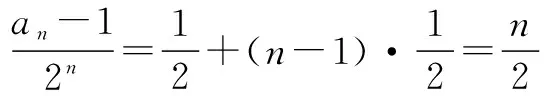
∴an=n·2n-1+1.

点评本题分两步，第一步处理常数-1，第二步等式两边同时除以2n+1，构造新的等差数列.

例6数列{an}满足an=2an-1+2n+1(n∈N*,n≥2),a3=27.

(1)求a1,a2的值；

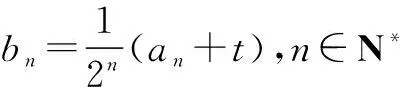
解(1)∵an=2an-1+2n+1,

令n=2,得a2=2a1+4+1=2a1+5.

令n=3,得

a3=2a2+9=2(2a1+5)+9

=4a1+19=27.

∴a1=2,a2=9.

(2)设an+m=2(an-1+m)+2n,

则an=2an-1+m+2n,∴m=1，

∴an+1=2(an-1+1)+2n.

等式两边同时除以2n,得