数学实验让课堂更有数学味——以“正方体表面的涂色问题”教学为例

石桂花



数学实验让课堂更有数学味
——以“正方体表面的涂色问题”教学为例

石桂花

数学家欧拉曾说：“数学这门科学需要观察，也需要实验。学生应重走人类掌握数学的历程，从直观具体的实验阶段走入抽象理论阶段。”审视目前使用的数学新教材，新增了实践与综合应用、直观与几何、几何变化、概率与统计等内容，这些内容的完成同样离不开实验。下面以苏教版教材六年级上册的思考题“正方体表面的涂色问题”教学为例，展示我们的研究过程和思考。

一、游戏导入，发现问题

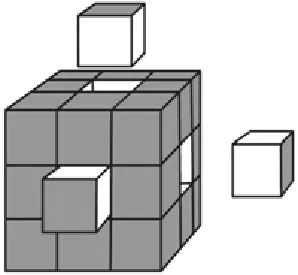
师：（展示一个由27个小正方体拼成的大正方体，表面被涂上颜色）同学们，这节数学课咱们来做点有趣的事情，玩魔方，怎么样？我给大家带来了一个大号的魔方。你知道它是由多少个这样的小正方体拼成的吗？是怎么算的？

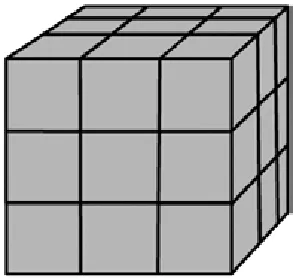
生1：这个魔方可以一眼就看出来，是由3×3× 3=27（个）小正方体组成的。

师：你说的3是指什么？

生1：3是指正方体的一条棱边有3个小正方体，它的棱长就是3个单位，所以可以这样计算。

师：说得真清楚。这个魔方就是一个棱长为3个单位的大正方体，它的表面，也就是6个面全部被涂上了蓝色。（把魔方举得更高给大家看，手不小心抖动了一下，魔方瞬间散掉了）啊呀，坏了！魔方散落了就玩不成了，怎么办呢？

生2：把它捡回来拼好，可以继续玩！（教师捡起散落的魔方拼摆好并展示在实物投影仪上）

生3：老师拼错啦，好多个位置都不对，那个3个面涂色的要拼在最上边的最外面。

生4：那个2面涂色的不能放在边上，要挪过去。

……

师：放错了呀！大家的意思是说这27个小正方体并不是6个面都被涂成了蓝色，不能随意摆放，对吧？那每一个小正方体可能有几个面被涂色？

生5：我看出来了，有3个面涂色、2个面涂色、1个面涂色的。（师随机板贴）

生6：我觉得，露在外面的至少都会有1个面涂色，最多的会有3个面涂色，它们在棱角顶点处。但是如果躲在正中间，就可能1个面也没涂上颜色。而且中间肯定藏着正方体，没有它摆在中间的话，上面这一个会塌陷下去，对吧？（师板贴没有涂色这种情况）

师：大家同意他们的观点吗？还有没有其他情况？

学生认真地观察投影仪上的正方体，都说“没有了”。

师：看来，要想还原这个魔方，就要考虑这里的每一个小正方体涂色的情况和它所摆放的位置以及个数。这就是我们这节课要研究的“正方体表面的涂色问题”。

设计意图：利用“散落的魔方玩不成了怎么办”的问题情境，引发学生的认知冲突，促使学生产生好奇心、求知欲和研究的兴趣。

二、分层研究，探索规律

（一）研究3×3×3的情况，初步感知规律

师：那这里的每一个小正方体表面的涂色情况和它所摆放的位置以及个数是怎样的呢？这个问题看起来还真有点复杂，怎么办呢？

生7：老师，要是我也有这样一个正方体可以看一看、数一数，就容易解决了。

生8：是的，要是能玩上一会儿，就会找到答案的。

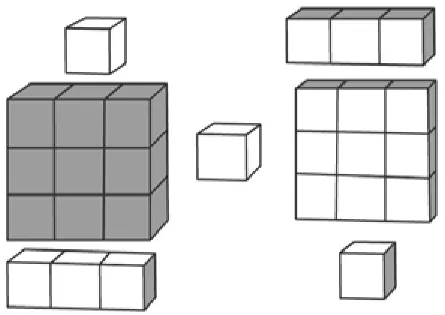
师：你们的建议真好！请大家拿出老师准备的表面涂色的3×3×3的魔方，同桌两人为一组开展研究，并请填写好实验记录单（如下所示）。

学生两人小组利用魔方学具帮助思考，开展合作研究，并认真地填写实验记录单，研究时间3分钟。

师：同学们研究得怎么样了？谁愿意来说说你们组的发现？

生9：我们把魔方转来转去，看了很久，又数了好几遍，发现3面涂色的在棱角顶点处，有8个。（板书：顶点处，8个）

师：为什么是8个？

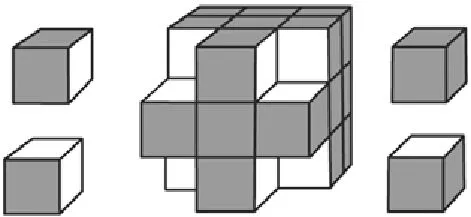
学生拿着魔方讲述理由。随着学生的描述，课件一个一个动态剥离棱角顶点处的小正方体，学生跟着课件寻找3面涂色的小正方体的位置以及个数。

师：其他4个顶点处的情况，大家可以自己想象一下。真了不起，大家找到了3面涂色小正方体的位置和个数。

生10：我们把魔方摸了又摸，转了又转，发现2面涂色的在大正方体的棱上。

学生拿着魔方讲述理由。随着学生的描述，课件一个一个动态剥离每条棱上的小正方体，让学生直观地看到2面涂色的小正方体的位置和个数。

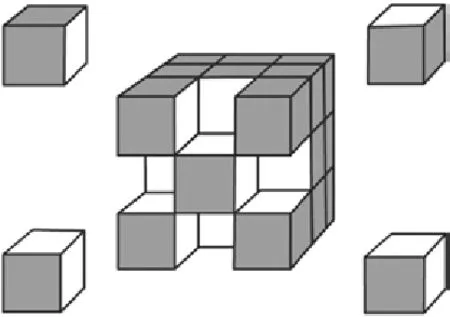
师：明明每条棱上有3个小正方体，为什么只有1个是2面涂色的？

生11：每条棱上是3个，但减去已经在棱角顶点上的3面涂色的2个，就只剩下中间这1个了。12条棱一共就有12个小正方体。

师：你的思路很清晰，说得也很清楚。看着课件再加上想象，2面涂色的12个找全了吗？那1面涂色的位于大正方体的什么位置？有几个？

生12：1面涂色的在每个面的中间，每个面上有1个，有6个面，所以有6个。

学生拿着魔方讲述理由。随着学生的描述，课件一个一个动态剥离前面、上面、右侧面中间的小正方体，学生清楚地看到1面涂色的小正方体的位置和个数。

师：怎么每个面只有1个1面涂色的小正方体呢？

生13：咱们看着魔方算一下就知道了。用棱长分别减去上下、左右两个已分别涂色的，就剩下中间位置的正方体，只有1个。

师：你很善于观察，善于总结，你的这个发现很重要。

生14：老师，我有更重要的发现，没有涂色的在正中心，只有1个呢。

师：哟，正中心的你都能看见，你有透视眼吗？

生14：不是。我刚才拿着魔方数了一下，发现看得见的小正方体只有8+12+6=26（个），还有1个不见了，所以肯定就藏在正中心，也就是没有涂色的只有1个！

师：你是通过计算算出来的，这是个好主意。其他同学得到的都是这样的结果吗？

生15：我是拿着魔方数的，确实缺少1个。然后自己想象，应该是有1个藏在正中心。

师：哦，是吗？边观察边想象可是解决问题的好办法。究竟是不是这样，我们一块看看：（课件动态演示）去掉前面一层，后面一层，上面一层，下面一层，左面一层，右面一层，中间就只剩下这1个啦！

师：要学好数学，解决问题后一定要验证答案。那你们的答案正确吗？怎么验证？

生16：算一算或者数一数就知道了，8+12+6+1 =27（个）。

生17：由27个小正方体组成的大正方体表面涂上颜色后，小正方体表面的涂色情况是这样的，3面涂色的有8个，2面涂色的有12个，1面涂色的有6个，没有涂色的有1个。

设计意图：通过实验操作发现的方式，学生经历“实物直观—观察发现—总结规律”的过程，把抽象的数学规律（每一个小正方体涂色的情况和它所摆放的位置以及个数）与直观的实物操作结合起来思考，对3×3×3的正方体表面涂色规律的探索自然水到渠成，教学做到了抽象与形象、做与思的结合。

（二）研究4×4×4的情况，总结发现规律

师：大家真是了不起，运用观察、操作等方法成功地解决了棱长为3个单位的正方体表面的涂色问题是与小正方体所在的位置有关，还与棱长有关。你们还想研究棱长为几个单位的正方体表面的涂色情况？（学生随意说：4个，5个，20个，100个）现在你们还需要提供正方体来研究吗？

生18：不用了，我们可以画一个立体图形，再加上自己的想象，就能找出规律。

师：大家的研究思路果然非常清晰。那我们再来研究棱长为4个单位的正方体表面的涂色情况。（课件出示棱长为4个单位的正方体）我指出几个位置的小正方体，请大家告诉我，它是几个面涂色的情况。

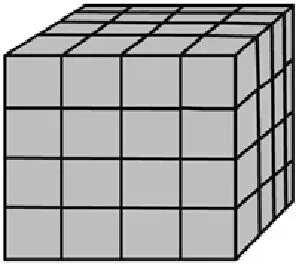
教师任意指这个正方体中的几个小正方体，学生分析涂色情况。

师：你们答得又快又好。那这一次我们抛开学具，拿出4×4×4的图纸，充分运用你的想象力，说出3面涂色、2面涂色、1面涂色以及没有涂色的小正方体分别在什么位置，各有多少个。

学生4人小组进行讨论交流，并填写好实验记录单。

师：哪一组汇报你们的发现？

生19：我们组发现3面涂色的还在棱角顶点处，有8个。（课件演示）2面涂色的还在大正方体的棱上，一条棱上有4-2=2（个），12条棱就有12×2=24（个）。

师：为什么会有24个？这个计算方法适合棱长为3个单位的正方体吗？（在学生计算认同后板书算式：（4-2）×12=24（个））现在我们看第三个问题，1面涂色的小正方体有几个？我们需要每个面都去计算吗？那如何计算呢？

生20：我们不需要每个面都计算，只需要观察大正方体1个面的规律就可以推算出6个面的情况。

师：是的，研究这个问题不必面面俱到，只要研究大正方体的1个面就可以了。（课件出示棱长为4个单位的正方体1个面的情况）

生20：从左往右看，本来每条棱上有4个，减去顶点处的2个3面涂色的，这一排就只有2个。从上往下看，本来也是4个，减去2个2面涂色的，也只有2层了。中间涂色部分所含的小正方体个数就是这个面1面涂色的正方体的个数。

师：你能用这个方法验证棱长为3个单位的正方体1个面的涂色情况吗？猜想一下棱长为5个单位的正方体1个面上有几个1面涂色的？（课件分别出示棱长为3、5个单位的正方体1个面的情况）

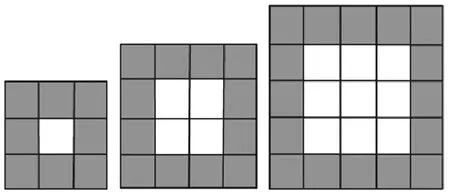
学生看图，想象后回答。

师：那没有涂色的又有几个呢？你是如何知道的？

生21：不需要找规律，64-8-24-24=8，是8个。

生22：我在脑子里用“剥”的方法想象了一下，也能知道有8个。左面去掉一层，右面去掉一层，上面去掉一层，下面去掉一层，前面去掉一层，后面去掉一层，剩下1个棱长为2个单位的正方体了。所以有2×2×2=8（个）。

生23：我只要“剥”去一层，看横截面中间的小正方体的个数就知道了。

师：你们真棒，刚学的方法就能学以致用了。大家也在脑子里“剥”上一“剥”。有困难的同学可以观看大屏幕上的演示一起验证。

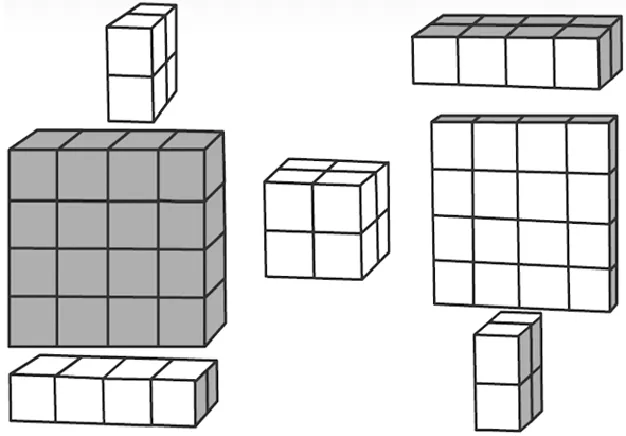
生24：我通过看课件演示明白了，没有涂色的小正方体藏在正中心。因为上下、左右、前后都被涂色了，剩下一个长、宽、高都是2个单位的正方体，只要用（4－2）×（4－2）×（4－2）=8，就是没有涂色的小正方体的个数。

师：大家能用这个规律验算棱长为3个单位的正方体表面的涂色情况吗？

学生验证后都点头表示可以。

师：同学们真了不起，又发现了棱长为4个单位的正方体表面的涂色情况。那刚才还有同学说想研究5个、100个甚至更多，我们继续往下一个一个研究吗？

学生纷纷摇头，大声说“不用了，不用了”。

师：那你们发现了正方体表面涂色问题的哪些规律呢？如果是棱长为N个单位的正方体，请你说说它表面的涂色情况又会是怎样的。（板书：N3（N×N× N））

生25：我来说最容易的3面涂色的情况。因为所有的正方体都是8个顶点，而3面涂色的在棱角顶点处，所以棱长为N个单位的正方体3面涂色的有8个。（板书：8）

师：祝贺大家发现了正方体表面涂色问题的第一个规律。棱长为N个单位的正方体2面涂色的有几个，你发现规律了吗？

生26：2面涂色的小正方体在棱上，与棱长有关系。棱长为4个单位的大正方体，2面涂色的有（4－2）×12=24（个）。那棱长为N个单位的大正方体，就用棱长N减去棱角顶点处的2个，再乘上12条棱就行了。（板书：（N-2）×12）

生27：棱长为N个单位的大正方体1面涂色的小正方体个数，从左往右看，本来每条棱上有N个，减去顶点处的2个3面涂色的，这一排就只有（N－2）个。从上往下看，本来也是N个，减去2个3面涂色的，也只有（N－2）层了。涂色部分所含的小正方体个数就是中间这个正方体的个数，等于（N－2）2个，有6个面，所以就是（N－2）2×6。（板书：（N－2）2×6）

师：那没有涂色的小正方体有多少个？

生30：没有涂色的在大正方体的正中心，也和棱长有关系。因为上下、左右、前后都被涂色了，中间就剩下一个长、宽、高都是（N－2）的正方体，只要计算（N－2）3，就能得到没有涂色的小正方体的个数。（板书：（N-2）3）

师：太佩服你们了，正方体表面的涂色问题这么难的一件事，被你们用实验研究的方法发现了规律，变成了一件非常容易的事，难怪老子说“世上无难事，只怕有心人”。

设计意图：数字资源呈现的实验活动要适量、适度。因而在学生的认识积累到一定程度时，要及时让学生的形象思维向抽象思维转化，实现活动的内化和思维的发展。因此，在总结“棱长为N个单位的正方体表面的涂色情况”的规律时，教师就采用了这一教学策略，促进了学生思维的发展。

三、总结下课，布置作业

师：同学们，就快下课了，你能说说你今天的收获吗？（学生积极地反馈这节课的收获，教师随机板书：实验探究、分类计数、数形结合、空间想象）

师：老师给每个4人小组都准备了一套由64个小正方体拼成的大正方体，表面涂上了红色。但是也散落了，装在了学具袋里。请你们将它恢复原状，看哪组同学合作得又快又好。

学生拿出学具袋，马上忙活起来：先将所有的小正方体分4类摆放，确认每种情况的个数后，再合作拼摆。最短的用时3分55秒，最长的用时5分20秒，都准确无误地还原了大正方体。

接下来课件出示：在一个正方体的表面涂上颜色，再把它切成棱长为1厘米的小正方体，已知2面涂色的小正方体有96个，求大正方体的棱长是多少厘米？

……

设计意图：在学生获得正方体表面的涂色规律后，教师并没有急于让学生简单地套用公式解决问题，而是让学生在总结归纳学习方法后，通过动手操作的方式将规律和方法内化。这样能让学生在记忆中对知识留下“刻痕”而不是“划痕”，同时培养学生的团队合作意识和能力。（本文系基金项目：湖南省教育科学“十二五”规划2015年度湖南省教育科学研究基地专项课题《信息化时代小学数学学科建设实践研究》成果，课题批准号：XJK015BJD038）

（作者单位：湘潭市雨湖区风车坪学校）