弦切角定理简化对带电粒子在磁场中运动的理解

◇　四川　龙　飘

弦切角定理简化对带电粒子在磁场中运动的理解

◇四川龙飘

带电粒子在匀强磁场中的运动分析是近几年高考的热点．要分析解决此类问题的关键是确定，在洛伦兹力作用下带电粒子的运动轨迹,一旦轨迹确定许多问题便可迎刃而解．众所周知,带电粒子在匀强磁场中的运动有以下2个基本结论:

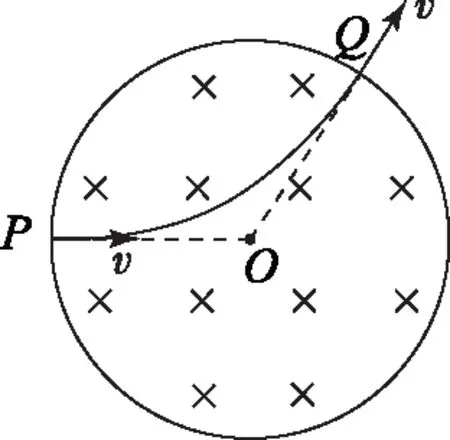
图1

结论1若带电粒子运动方向沿半径方向射入具有圆形边界的匀强磁场,则其射出磁场时的速度方向反向延长线必过圆心(如图1)．

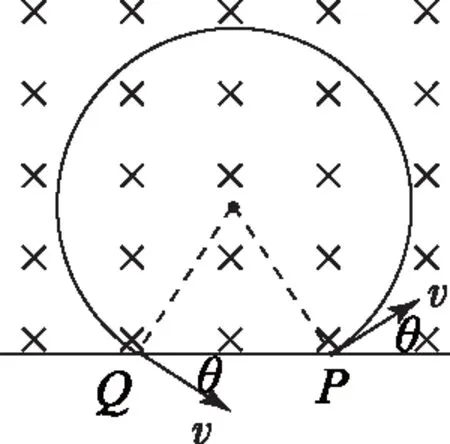
图2

结论2若带电粒子运动方向沿匀强磁场的直线边界射入，又从该边界射出,则其轨迹入射速度方向和出射速度方向与边界的夹角相等(如图2)．

以上2个结论对找出带电粒子在磁场中运动轨迹,分析解决相关题型非常重要．教材并没有给出严谨的证明,因此很多学生无法完整理解和应用这2条结论．本文从纯数学的角度对以上2个结论进行论证．

图3

1结论1的证明

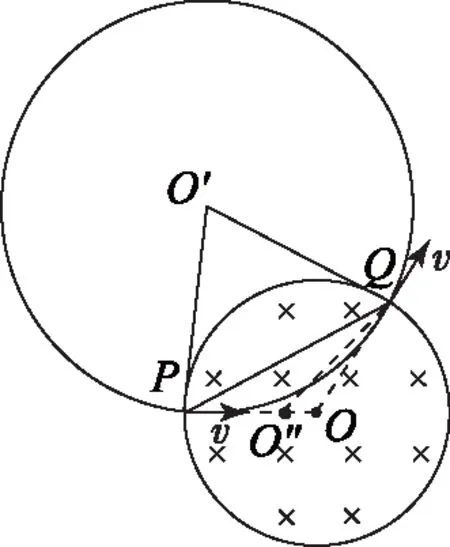
图4

如图3,带电粒子沿半径方向从P点射入圆形边界匀强磁场,并从Q点射出．如图4,将其运动轨迹圆弧以及圆弧所形成的完整的圆形补全则得到圆O′,连接PO′、QO′可知PO′=QO′,延长P点速度方向交圆心O点且O′P⊥OP．

反向延长Q点速度方向,设交PO所在直线于O″,即O′Q⊥O″Q．连接PQ,在等腰△O′PQ中∠O′PQ=∠O′QP,得∠QPO=∠PQO″,即△PQO″为等腰三角形．若过O″点作O″M⊥PQ交PQ于M,则O″M为PQ中垂线所在直线．因为PQ为圆O的一段弦,则PQ中垂线必过圆心O,即交点O″必与圆心O重合．故结论1成立．同时也可知O′Q、O′P为圆O上弦P、Q两点的切线,进而得出:在同一圆中一条弦与圆弧两交点切线分别形成的弦切角相等．

2结论2的证明

根据以上得出的“在同一圆中一条弦与圆弧两交点切线分别形成的弦切角相等”,便可证明结论2．

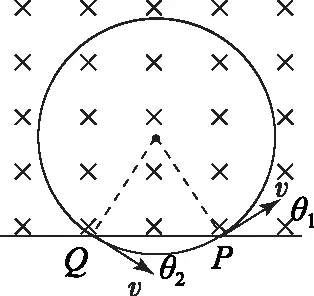
图5

如图5所示,同样的将在磁场外与磁场内圆弧轨迹相吻合的圆弧补充完整,则PQ为圆轨迹的一段弦,入射磁场速度方向和射出磁场速度方向所在直线分别与轨迹圆相切于P、Q两点,则θ1与θ2分别为同一圆中一条弦与圆弧两交点切线分别形成的弦切角,则有θ1=θ2．结论2成立．

3结论的运用

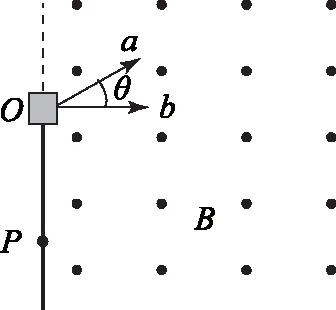
图6

Aa、b均带正电;

Ba在磁场中飞行的时间比b的短;

Ca在磁场中飞行的路程比b的短;

Da在P上的落点与O点的距离比b的近

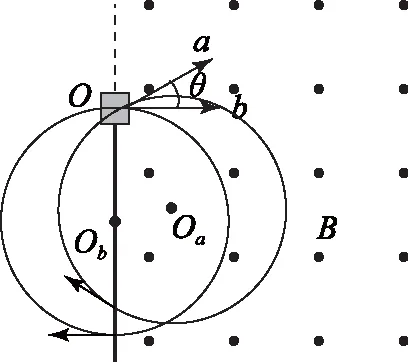
图7

分析由左手定则可知，选项A正确.经过同一匀强磁场直线边界,入射磁场时速度方向与边界的夹角必定与射出磁场速度方向与边界夹角相等．由此得a离子射出磁场边界的点到O的轨迹为运动轨迹圆的一段弧,而垂直入射的离子射出的速度方向也应与边界垂直,所以射出点到O的距离为圆形轨迹的直径,因为这2个离子相同且初速度相同，由此可知二者运动轨迹半径相同．故选项D正确．

在讲解以上2条结论时，教师可以启发学生通过以上证明得到弦切角相关性质，从而巩固对此结论的理解,使学生将物理与数学知识互相渗透，从而可以更加快速地解答有关带电粒子在磁场中运动轨迹类的问题．

(作者单位：西华师范大学)