块严格γ -链对角占优矩阵的新判据

蒋建新

(文山学院 数学学院，云南 文山 663000)



块严格γ -链对角占优矩阵的新判据

蒋建新

(文山学院 数学学院，云南 文山 663000)

摘要：通过对分块矩阵的指标集进行划分，利用块严格γ -链对角占优矩阵的定义和性质，并使用不等式的放缩方法，得到判定块严格γ -链对角占优矩阵只与元素有关的条件.

关键词：块H-矩阵；块对角占优矩阵；块严格γ -链对角占优矩阵

块对角占优矩阵在数学、系统理论等诸多领域有着广泛的应用，但如何简便的判别一个矩阵是否是块对角占优矩阵一直是人们关注的问题，关于这类问题许多学者都进行了研究[1-4]. 学者们对于这些矩阵的判定，主要思想是构造只与矩阵元素有关的判据，从而使操作性更高. 但对块对角占优矩阵新的子矩阵块γ -链对角占优矩阵的判定，除了定义外，并没有给出其它的判定定理. 本文利用研究其它块对角占优矩阵判据的思想，研究块严格γ -链对角占优矩阵的新判据.

1　预备知识

设Cn×n表示复(实)矩阵的集合，分块为

Aii是非奇异的ri阶方阵，1≤i≤n，且

定义2 对于分块矩阵A，若存在γ ∈[0,1]，使对∀i∈N，有成立，称A为块γ-链对角占优矩阵；若上式中的等号是严格的，则称A为块严格γ -链对角占优矩阵[6].

引理1 对于分块矩阵A，若A为块严格γ -链对角占优矩阵，则A是块H-矩阵[6].

2　块严格γ -链对角占优矩阵的判定

本部分通过对分块矩阵的指标集进行划分，利用块严格γ -链对角占优矩阵的定义和性质，并使用不等式的放缩方法，得到了判定块严格γ -链对角占优矩阵的只有元素有关的条件.

定理1 设A=(aij)∈ Cn×n，若存在γ ∈[0,1]，使A满足下列条件之一，A即为块γ -链对角占优矩阵. 则

其中

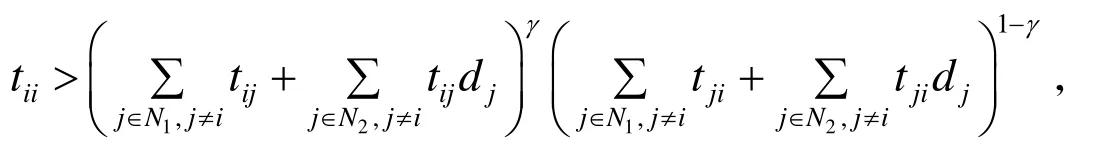
证明：先证条件1)

如果条件1)成立，则di>0 (i∈N2)，且. 由di的定义知

对任意的i∈N1，有

对任意的i∈N2，有

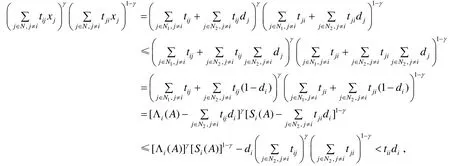
其次证条件2)

如果条件2)成立，则di>0 (i∈N2)，且

. 由di的定义知

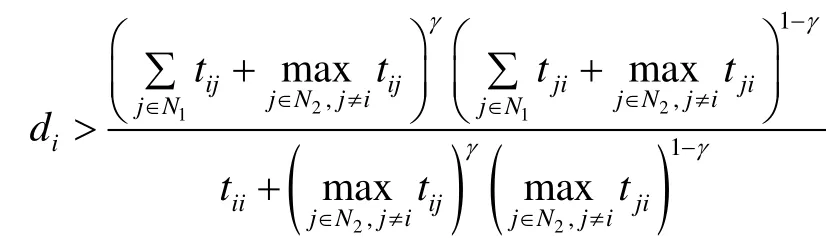
对任意的i∈N1，有

对任意的，有

. 所以XAX是块严格γ - 链对角占优矩阵. 即A是块γ - 链对角占优矩阵，进一步是块H-矩阵.

注：本文定理1中给出的两个新的判断矩阵是否是块γ -链对角占优矩阵的估计式，与文中定义2相比，只与矩阵的元素有关，易于计算.

参考文献：

[1] 高会双. 块H矩阵的判定和应用[J]. 重庆师范大学学报: 自然科学版, 2015(2): 99-103.

[2] 崔晓梅, 许 洁. 块广义严格对角占优矩阵的判定准则[J]. 吉林化工学院学报, 2014(7): 82-83.

[3] 高会双, 韩贵春, 肖丽霞. 块α对角占优矩阵的讨论[J]. 纯粹数学与应用数学, 2014(1): 53-59.

[4] 李艳艳. 非奇异块α1对角占优矩阵新的实用简介判据[J]. 文山学院学报, 2012(6): 37-41.

[5] 黄庭祝, 杨传胜. 特殊矩阵分析及应用[M]. 北京: 科学出版社, 2006: 1-4.

[6] 薛 媛, 刘建州. γ -链对角占优矩阵与H-矩阵的判定[J]. 工程数学学报, 2015(5): 709-718.

(责任编辑：饶 超)

New Criterion for Block Strictlyγ-diagonally Dominant Matrix

JIANG Jianxin
(School of Mathematics, Wenshan University, Wenshan 663000, China)

Abstract:Classified by block matrices of the index set， by using some definition and properties of block γ -diagonally dominant matrix, using inequality scaling method, it got the conclusion that judging block strictly γ -diagonally dominant matrix was just related to the elements.

Key words:Block H- matrix; Block diagonally dominant matrix; Block strictly γ -diagonally dominant matrix

中图分类号：O151.21

文献标志码：A

文章编号：2095-4476(2016)05-0009-03

收稿日期：2016-02-29

作者简介：蒋建新(1981— ), 男, 甘肃天水人, 文山学院数学学院讲师.