倾转旋翼机模态转换的鲁棒H∞增益调度控制

蔡系海,付　荣,曾建平

(厦门大学航空航天学院,福建厦门361005)

倾转旋翼机模态转换的鲁棒H∞增益调度控制

蔡系海,付荣,曾建平*

(厦门大学航空航天学院,福建厦门361005)

摘要：研究了某小型倾转旋翼无人机模态转换阶段的飞行控制问题．基于鲁棒H∞控制,给出了一种模态转换飞行的增益调度方法,其设计条件具有线性矩阵不等式(LMI)的形式．针对模态转换飞行阶段存在的操纵冗余问题,给出了一套实用的舵效分配策略．通过对该飞行器转换模态纵向动力学系统进行仿真研究，结果表明,该方法可以确保飞行器能准确地按照预定轨迹完成模态转换飞行,并对模型中存在的气动参数摄动具有较好的鲁棒性,且能够有效地抑制阵风等外部扰动．

关键词：倾转旋翼无人机;控制分配;增益调度;鲁棒H∞控制

倾转旋翼机是一种独特的飞行器,它在常规固定翼飞机的基础上安装了可倾转的旋翼，因此,它既具有像直升机一样垂直起降、悬停和低空低速飞行的能力,又具有像固定翼飞机一样的高速和远距离巡航能力[1]．鉴于这些优势,该机型引起了国内外研究人员的广泛兴趣,并取得了一系列成果．20世纪50年代由贝尔直升机公司设计的XV-3验证了倾转旋翼机的原理[2]．在XV-3的基础上,1973年该公司又设计了方案验证机XV-15,该机型可以验证倾转旋翼机方案的可行性和任务的适应性[3]．1983年该公司和波音公司开始研制军用型V-22“鱼鹰”[4]倾转旋翼机．为进一步探索倾转旋翼技术,土耳其学者Cetinsoy设计了一架油电混合动力的具有变形机翼的倾转四旋翼无人机,在综合考虑旋翼倾转受力、油量变化和机翼变形的影响后,建立其非线性动力学模型,分析了该机的控制策略．Kendoul等学者针对拥有1对能够纵向和横向偏转旋翼的倾转旋翼无人机,验证了使用双旋翼进行悬停的可行性,并使用back-stepping方法设计了无人机的增稳和轨迹跟踪控制器．近10年来,我国开始重视倾转旋翼机的研究,并在旋翼/机翼气动干扰[7-8]、旋翼/短舱/机翼耦合气弹稳定性[9]、倾转过程飞行控制方法[10]等方面取得了阶段性成果．

倾转旋翼机因其独特的构造使其气动特性和稳定性会随着倾转角的改变发生显著的变化,其变化过程不仅是时变的,还是强非线性、强耦合的,整个模态转换飞行阶段存在严重的操纵冗余问题．国外虽已有这些方面的研究,并取得了大量的实验数据[3],但因涉及过多的倾转旋翼飞行器核心技术机密,并没有太多资料可查阅．

本文以某小型倾转旋翼无人机纵向系统模型为研究对象,采用传统增益调度方法完成飞机模态转换飞行控制．考虑到气动参数摄动和阵风干扰,在各工作点设计了鲁棒H∞控制器[11]．针对该类飞行器既具有拉力矢量操纵又存在气动舵操纵的复杂特性,给出了一套实用的舵效分配方案．最后,通过数字仿真验证该控制方案的有效性．

1倾转旋翼无人机纵向模型

1.1转换模态纵向动力学方程

图1　无人倾转旋翼机机体轴示意图Fig.1Body axis of tilt rotor unmanned aerial vehicle

倾转旋翼无人机含有直升机模态、固定翼模态和介于两者之间的转换模态3种不同的飞行方式．如图1所示,该飞行器在常规固定翼飞机机翼内侧装有可倾转的栅板,并在两侧栅板上安装旋翼.随着栅板的倾转,旋翼的方向发生改变，从而改变飞机的飞行模态．

以油门中值δpe、升降舵偏δz和倾转角中值δte为输入,以速度V、迎角α、俯仰角ϑ、俯仰角速率q以及高度H为状态量,倾转旋翼无人机纵向动力学方程为

(1)

其中,m为飞行器的质量,Iz为俯仰转动惯量,Fxt和Fyt为机体所受到合力在机体轴系xt和yt轴的分量,Mz为合力产生的俯仰力矩,可表示为

Mz=MzJ+MzX+MzS.

其中MzJ、MzX和MzS分别为机体气动力、旋翼拉力以及栅板气动力产生的俯仰力矩．

倾转旋翼机所受的合力包括机体气动力、旋翼拉力、机身重力以及栅板气动力．机体阻力Q、升力L以及机体气动力产生的俯仰力矩MzJ分别为：

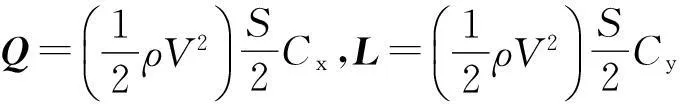
其中,Cx、Cy分别为机体对应的阻力系数和升力系数,ρ为给定高度的大气密度,S为机翼面积,mz为机体俯仰力矩系数,bA为平均气动弦长．

左右旋翼所产生的拉力TL和TR,以及旋翼产生的俯仰力矩MzX分别为：

TL=14.75δpL-0.819,

TR=14.75δpR-0.819,

MzX=-TLcos(τLyT)-TRcos(τRyT)．

其中,δpL、δpR分别表示左右油门,τL、τR分别表示左右栅板倾转角大小,yT为旋翼拉力作用点相对重心的垂向位置．

栅板气动力和力矩表达形式与机体气动力及力矩表达式基本一致,只是对应的力和力矩系数不一样,限于篇幅不再一一列出．

倾转旋翼机根据旋翼的状态分为3种飞行模态,不同的飞行模态对应的控制输入也不相同．当飞机处于直升机模态时,纵向主要以δpe和δte控制为主;处于固定翼模态时,纵向控制操纵变量主要以δpe和δz为主;处于模态转换阶段时,固定翼气动舵和直升机的旋翼拉力矢量2套操纵机制同时存在,即整个飞行过程中存在操纵冗余．倾转角τ=0°时为固定翼飞机模态,τ=78°时为直升机模态．在模态转换飞行阶段,以τ的变化引导飞机模态的转换．为了模态转换平稳安全,本文采取定高模态转换飞行．δpe和δte可以表示为：

在设计控制器时,为解决转换飞行阶段的操纵冗余问题,给出以下假设:

1.2线性不确定性模型

(2)

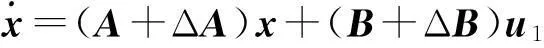
(3)

为了简化控制器设计,根据假设1,引入虚拟控制输入,则式(3)可改为

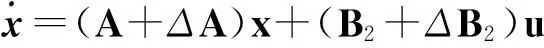
(4)

(5)

式中,E、Fa和Fb是适维已知矩阵,反映了不确定参数的结构信息,Σ为适维不确定矩阵,且满足

其中I为单位矩阵．

参考文献[12]方法,倾转旋翼无人机纵向线性化不确定性模型(4)的结构参数矩阵可选为

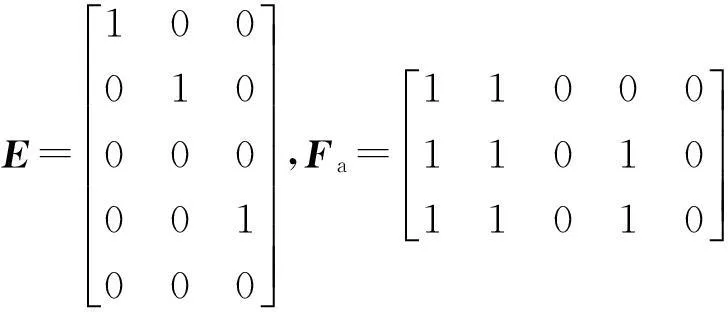
注1相比于区间描述法,上述参数不确定性刻画的保守性较小．该方法的关键是找出引起参数摄动的外界因素σ和摄动参数之间的关系．这时不确定矩阵就是关于σ的一些函数,摄动结构阵E、Fa、Fb均为一些低阶矩阵,可有效减小计算量．

1.3鲁棒H∞控制问题

飞机在飞行过程中会受到许多环境因素的影响,从而影响飞行品质,在这里统一把这些因素以及未建模动态视为系统的外部扰动,则系统(3)可改进为

(6)

其中,B1为扰动输入矩阵,w为外部扰动信号．

对于任意给定的h>0,设w满足

对给定的加权阵Q≥0和R>0,标量γ>0,H∞控制是指设计控制器u=Kx,使闭环系统内稳定,且对于任意给定的h>0,有

(7)

加权矩阵可用来调节干扰抑制效果和控制输入指令之间的关系,γ(>0)越小意味着系统对w的抑制性能越好．定义被控输出信号为

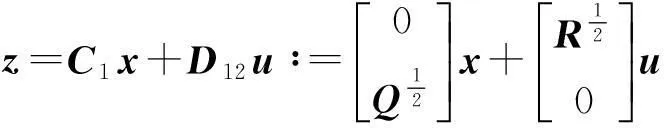
(8)

联立方程(6)和方程(8),可得广义被控对象为

(9)

2倾转旋翼无人机鲁棒H∞增益调度设计

倾转旋翼无人机随着倾转角的改变动力学特性发生较大变化,而增益调度(gain-scheduling)控制被认为是处理该类控制问题十分有效的方法[13]．

增益调度的基本思想是:先选取能够覆盖整个飞行包线的工作点,并通过小扰动线性化得到各工作点处线性模型;然后使用线性控制理论设计相应的控制器使其满足一定的飞行品质标准;最后将所得控制器采用切换或插值拟合的方法拟合成一个含有调参变量的全局控制器,进而实时调节控制器增益以适应飞机动力学模型的变化．根据上文对倾转旋翼无人机模型的分析,针对各工作点的线性化模型,本文采用鲁棒H∞增益调度的设计方法．

2.1鲁棒H∞增益调度设计

在综合考虑了倾转旋翼无人机模态转换飞行阶段存在参数摄动、外部干扰和本身复杂的气动特性情况下,设计鲁棒H∞增益调度控制器，使得该飞行器能按照预定的轨迹完成模态转换飞行,并能有效地处理参数不确定问题和抑制外部扰动．整个飞行过程以倾转角τ为调参变量,控制系统结构图如图2所示.

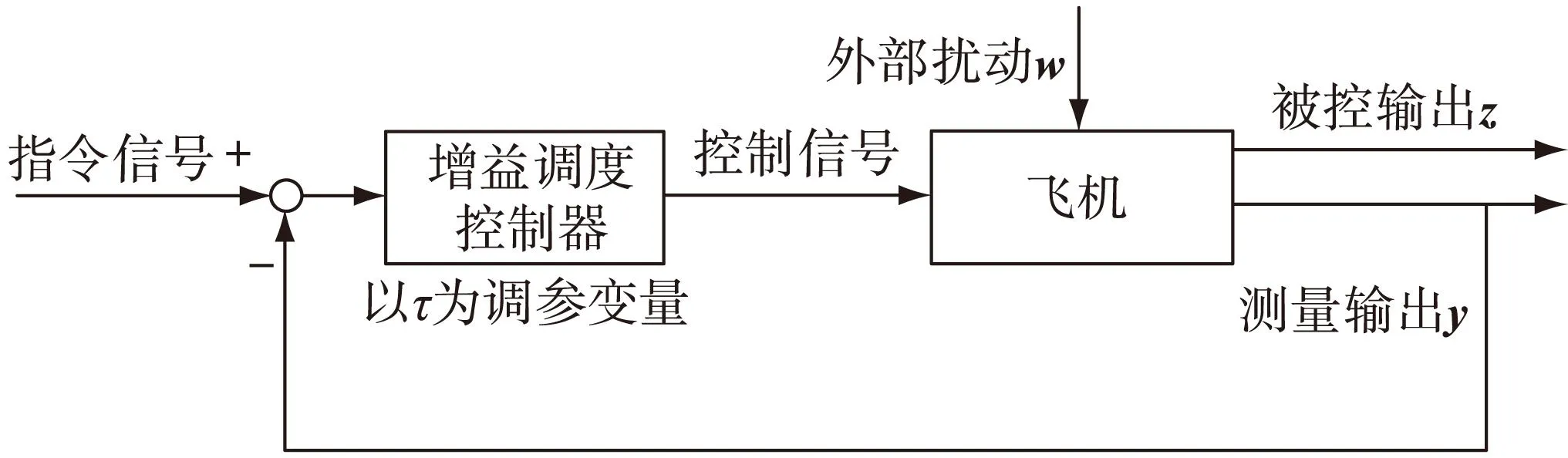
图2　控制系统结构图Fig.2Block diagram of control system

引理1[14]设Y为对称矩阵,N1,N2为适维常值矩阵,Σ为适维不确定性矩阵,且满足ΣTΣ≤I,则以下命题等价：

1) Y+N1ΣN2+(N1ΣN2)T<0，

应用引理1和有界实引理,可建立广义被控对象(9)的鲁棒H∞增益调度控制的可解性条件．

定理1给定扰动抑制水平γ>0,如果存在正定对称矩阵X和W,正常数ε,使得不等式

<0

(10)

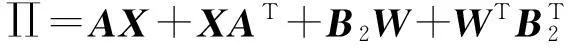
进而,如果X*,W*是矩阵不等式(10)的一个可行解,则K=W*(X*)-1是系统(9)的一个状态反馈H∞控制器增益矩阵．

证明对于系统(9),采用状态反馈u=Kx,则闭环系统为

(11)

其中,Ac=A+B2K,Cc=C1+D12K,ΔAc=EΣFc,Fc=Fa+FbK．

由有界实引理易知,若存在对称正定矩阵P,使得

(C1+D12K)T(C1+D12K)+PEΣFc+

(EΣFc)TP<0

(12)

成立,则系统(11)内部渐近稳定,且H∞范数小于γ．

由引理1知式(12)等价于

(C1+D12K)T(C1+D12K)+εPEETP+

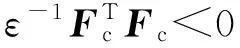
(13)

对上式两端同乘P-1,并令P-1=X,W=KX,则

D12W)T(C1X+D12W)+εEET+ε-1(FaX+

FbW)T(FaX+FbW)<0.

(14)

根据Schur补引理可知,不等式(14)等价于线性矩阵不等式(10)．证毕．

以倾转角τ为控制器增益调参变量,选取s个平衡点作为工作点．按照定理1设计鲁棒H∞控制器,设每个工作点的控制器为

u=Klx，l=1,2,…，s.

(15)

对于所求得的控制器增益Kl,以τ为自变量,利用插值拟合的方法得到全局控制器增益矩阵结构如下:

(16)

2.2控制分配

1) 在τ>60°时,速度较小,升降舵效低,虚拟升降舵指令完全分配给倾转角中值控制无人机的俯仰运动;15°<τ≤60°时,虚拟升降舵指令经过比例分配,产生实际的升降舵指令和倾转角指令,实现对俯仰运动的混合控制;0°≤τ≤15°时,此时飞行速度较大,倾斜角中值控制效率低,完全采用升降舵控制飞机的俯仰运动．

2) 整个模态转换阶段虚拟油门指令产生实际所需的油门中值指令．

设虚拟升降舵将操作效率的Kz(τ)倍由升降舵承担,将操作效率的KTz(τ)倍由δte承担,则可确定操作效率分配系数如下:

KTz(τ)=

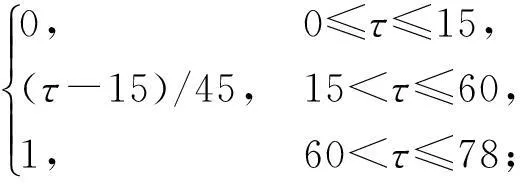
(17)

Kz(τ)=1-KTz(τ).

(18)

(19)

(20)

式(20)中,Kδz、Kδte分别表示虚拟升降舵到升降舵和倾转角中值的传递系数,表示为

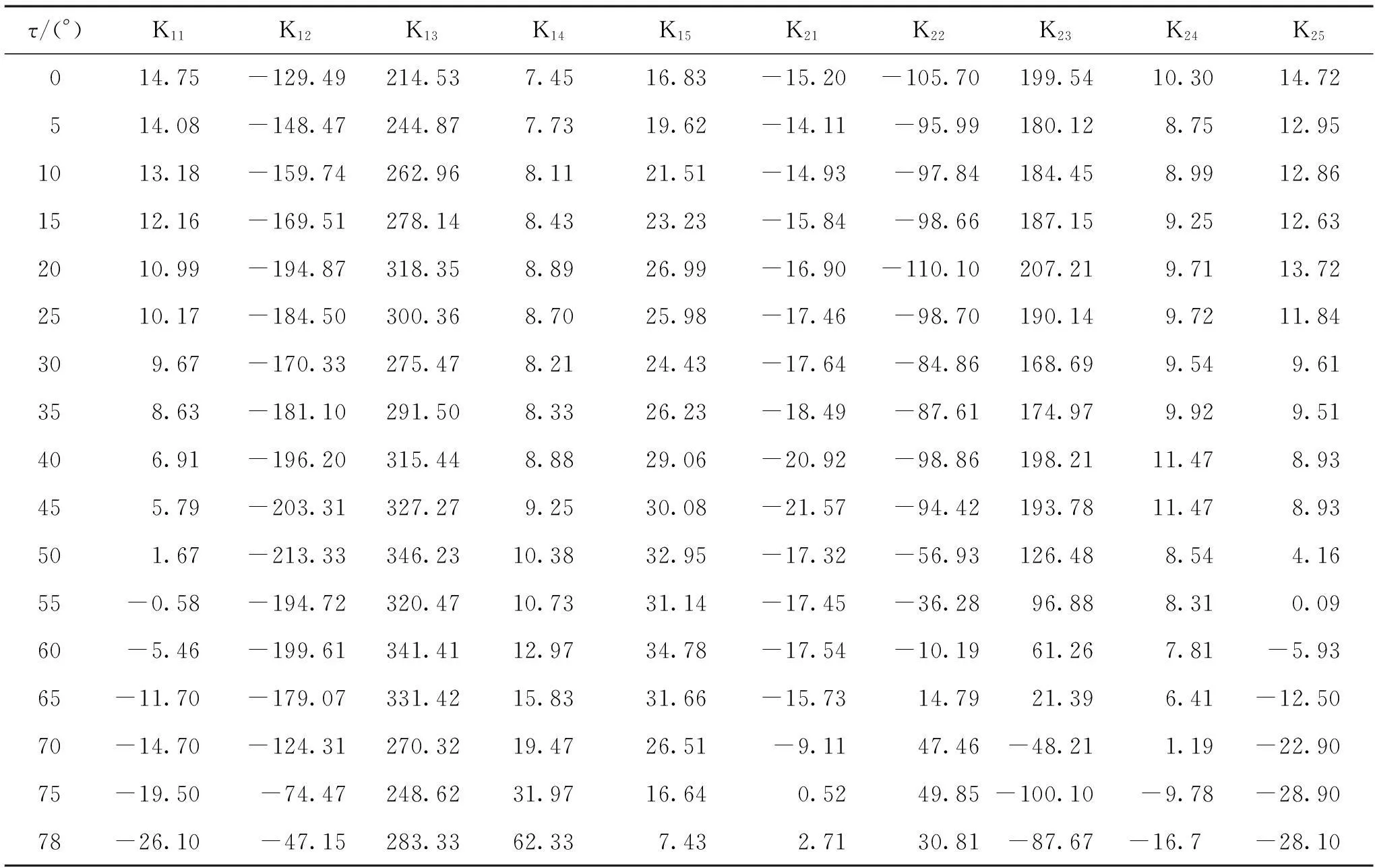
表1　控制器增益调度表

注：τ=78°时对应的模态即为直升机模态，表示由固定翼向直升机模态倾转完成.

3仿真及分析

某倾转旋翼无人机的基本参数如下:m=2kg,Iz=0.051 4kg·m2,bA=0.21m,S=0.233m2,yT=0.055m,ρ=1.225kg/m3．以倾转角τ每倾转5°作为一个工作点,按照定理1设计鲁棒H∞控制器,得到控制器增益调度表，如表1所示.

根据增益调度表,使用插值的方法,以倾转角τ为调参变量,拟合得到控制器增益调参曲线表达式如下:

K11=-1.017×10-4τ3+3.822×10-3τ2-

0.194τ+14.73，

K12=4.491×10-5τ4-5.538×10-3τ3+

0.243τ2-5.422τ-128.6，

K13=-2.831×10-5τ4+3.977×10-3τ3-

0.216τ2+6.578τ+217.1，

K14=1.582×10-5τ4-1.98×10-3τ3+

0.077τ2-0.929τ+9.458，

K15=-1.157×10-5τ4+1.507×10-3τ3-

0.063τ2+1.193τ+15.9，

K21=2.377×10-4τ3-0.018τ2+0.248τ-

15.45，

K22=-4.962×10-5τ4+7.573×10-3τ3-

0.318τ2+4.256τ-110，

K23=4.997×10-5τ4-8.626×10-3τ3+

0.386τ2-5.322τ+201.9，

K24=-2.804×10-4τ3+0.024τ2-0.512τ+

11.23，

K25=-1.345×10-4τ3+3.55×10-3τ2-

0.051τ+13.64.

同时,按照第3部分所给出的分配策略,得到控制分配系数为

将所得到的虚拟操纵舵面指令按给出的控制分配策略分配给实际操纵面,用于驱动飞行器运动,以验证所设计控制器的性能．具体指令为:随着飞机以直升机模式加速前飞,栅板以1(°)/s向前倾转,倾转旋翼机开始从直升机模态向固定翼模态过渡,78s后转入固定翼飞行并短暂飞行10s,再由固定翼模态反向过渡到直升机模态,在t=166s时飞机转换模态飞行完成,倾转旋翼机进入直升机模态且保持3m/s匀速飞行14s,全程仿真时间180s．

此外,整个仿真过程中气动力系数Cx、Cy及力矩系数mz反向引入30%的参数摄动,且在t=50s时加入幅值为2m/s的半正弦阵风,作用时间3s．状态初始值取为:V=3m/s,α=ϑ=0.026 5rad/s,q=0,H=20m．仿真结果如图3～10所示.

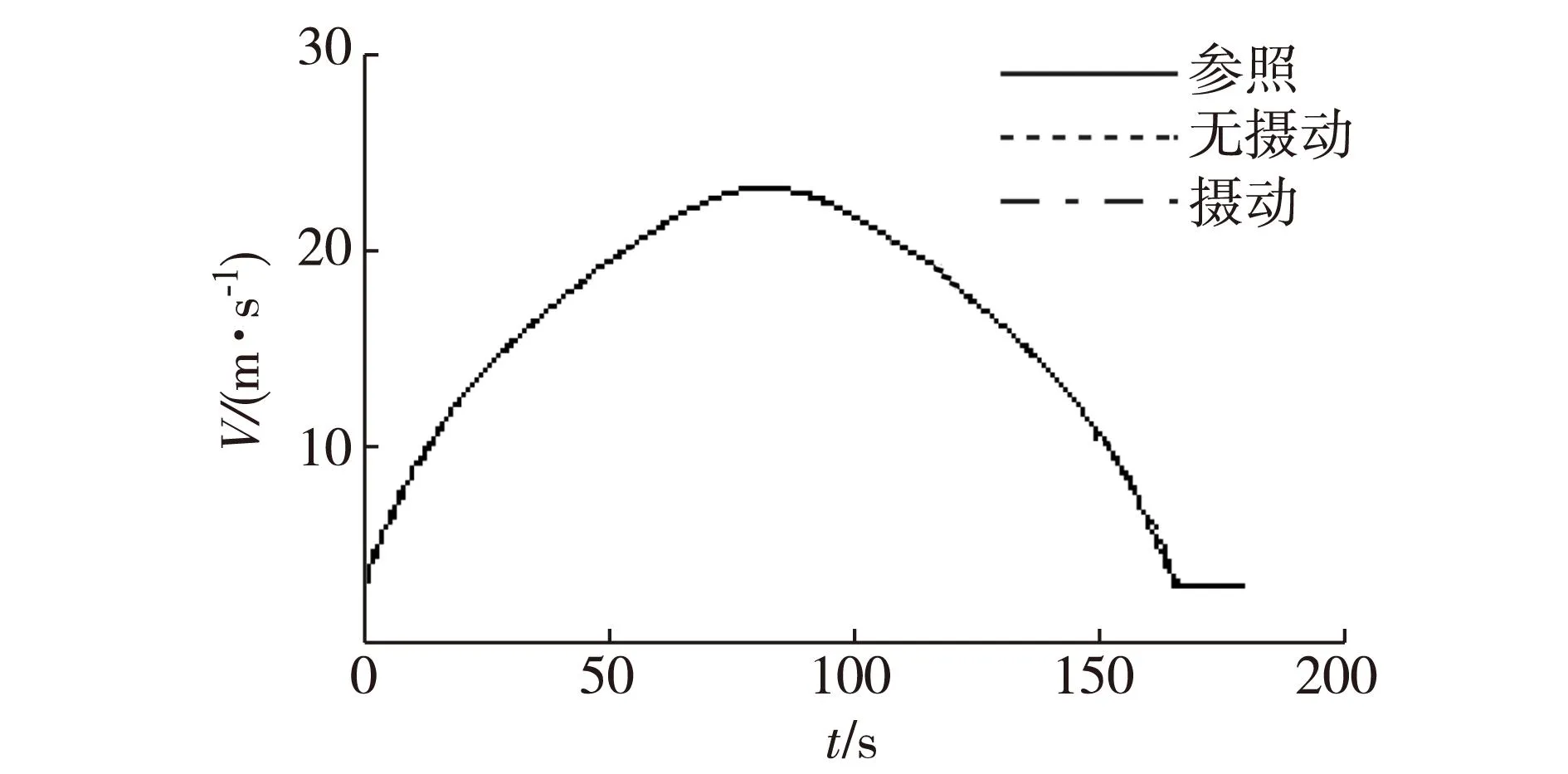
图3　速度指令跟踪曲线Fig.3Velocity command tracking curve

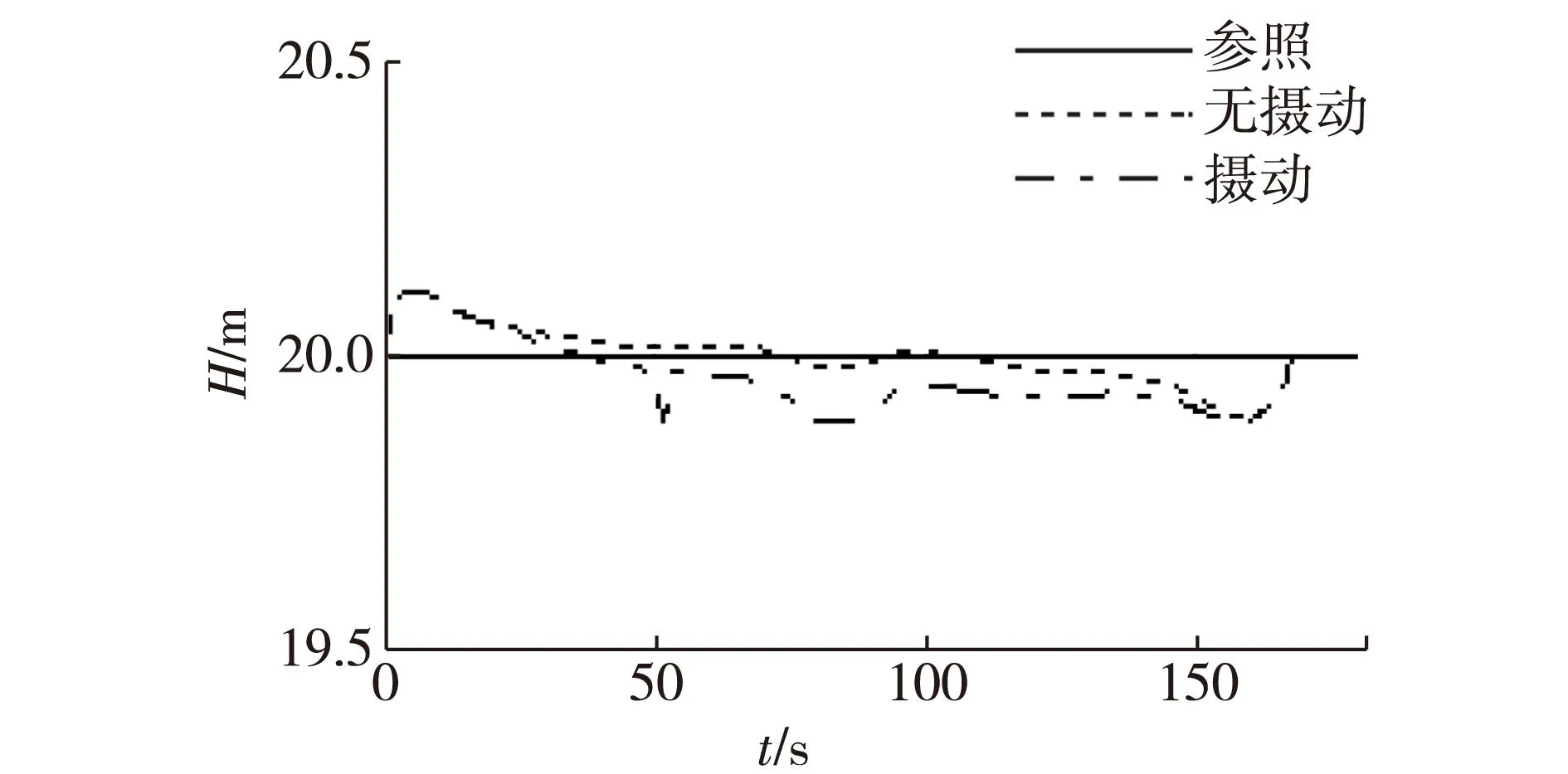
图4　高度指令跟踪曲线Fig.4Altitude command tracking curve

图5　迎角响应曲线Fig.5Angle of attack response curve

图6　俯仰角响应曲线Fig.6Angle of pitch response curve

图7　俯仰角速率响应曲线Fig.7Angle of pitch rate response curve

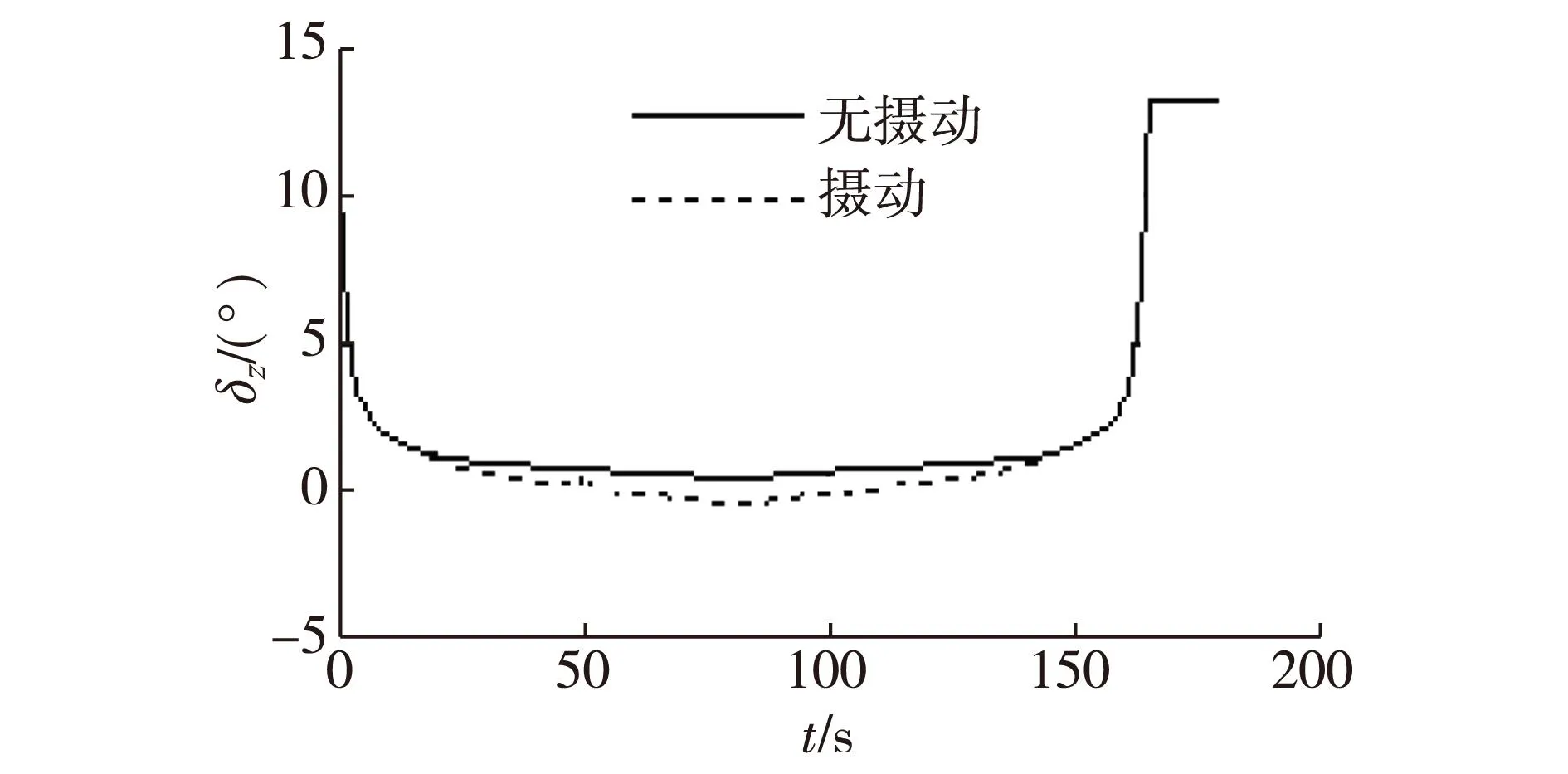
图8　升降舵偏角响应曲线Fig.8Elevator deflection response curve

图9　油门开度响应曲线Fig.9Throttle response curve

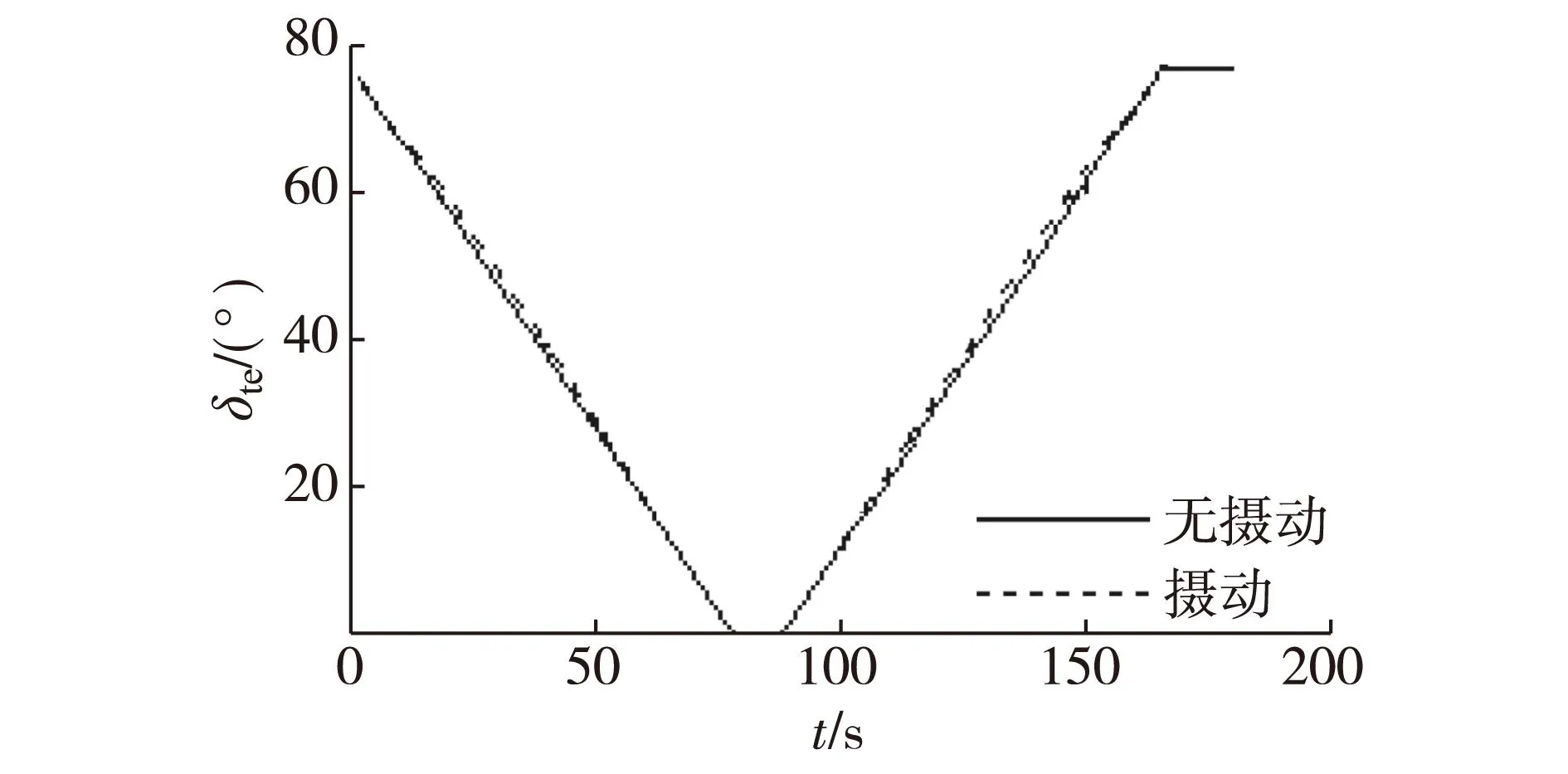
图10　倾转角中值响应曲线Fig.10Tilting angle response curve

针对倾转旋翼无人机纵向运动不含参数摄动和含摄动、阵风干扰的2种情况,图3和图4分别给出了鲁棒控制器作用下V和H的跟踪效果,图5～7分别给出了飞行器α、ϑ和q的响应结果,图8～10分别给出了δz、δpe以及δte控制输入响应．

分析图3～7可知:

1) 当系统模型存在较大的不确定性以及阵风干扰时,系统的动态性能虽然受到一定的影响,但最终速度跟高度的跟踪误差能得到消除;

2) 由于气动参数反向摄动,为了提供足够的气动力,α有所增大,ϑ也相应增加,但变化都在安全范围内,整个过渡阶段平滑稳定,表明本文所设计的控制器具有较好的鲁棒性及抗干扰能力．

分析图8～10可知,δz、δpe以及δte都较合理,表明控制器设计的优良性．

综上分析,本文设计的鲁棒H∞增益调度控制器能有效地处理气动参数摄动和阵风引起的干扰,并能确保倾转旋翼无人机按预定的轨迹完成模态转换飞行．

4结论

本文研究了某小型倾转旋翼无人机模态转换飞行阶段的飞行控制问题,针对该类飞机的强非线性、强耦合和时变等特性,将增益调度策略应用于控制器设计．考虑到模态转换飞行过程中存在着较大的参数摄动和阵风干扰,基于平衡点线性化模型设计了单个工作点的鲁棒H∞控制器,并将控制器求解条件转化为求解线性矩阵不等式(LMI)．此外,为了解决模态转换飞行时存在的操纵冗余问题,文中还给出了一套舵效分配控制方案．仿真实验表明,文中方法设计的倾转旋翼无人机模态转换飞行控制系统满足性能指标要求,对系统模型中的参数摄动具有较好的鲁棒性,可有效抑制阵风等外部干扰．

[1]杨军,吴希明,凡永华等．倾转旋翼机飞行控制[M]．北京:航空工业出版社,2006:1-37.

[2]THOMPSONTH．ThebellhelicopterXV-3andXV-15experimentalaircraft[R]．WashingtonDC:AIAA,1990.

[3]MAISELMD,GIULIANETTIDJ,DUGANDC．ThehistoryofXV-15tiltrotorresearchaircraftfromconcepttoflight[R]．WashingtonDC:NASAAmesResearchCenter,2000.

[4]蔡婧,蔡汝鸿．V-22“鱼鹰”倾转旋翼机研制历程与关键技术[J]．航空科学技术,2013,3(1):11-14.

[5]CETINSOYE．Designandmodelingofagas-electrichybridquadtilt-rotorUAVwithmorphingwing[C]∥Proceedingsof2014IEEEInternationalConferenceonMechatronicsandAutomation.Tianjin,China:IEEE,2014:1193-1198.

[6]KENDOULF,FANTONII,LOZANOR．Modelingandcontrolofasmallautonomousaircrafthavingtwotiltingrotors[C]∥Proceedingsofthe44thIEEEConferenceonDecisionandControl,andtheEuropeanControlConference．Seville,Spain:IEEE,2005:8144-8149.

[7]曹芸芸．倾转旋翼飞行器旋翼对机翼向下载荷计算模型[J]．航空动力学报,2011,26(2):468-147.

[8]郭建东,宋彦国．小型无人倾转旋翼机气动与操纵特性实验研究[J]．空气动力学报,2013,33(1):107-112.

[9]DONGLH,YANGWD,XIAPQ．Multi-bodyaeroelasticstabilityanalysisoftiltrotoraircraftinhelicoptermode[J]．TransactionsofNanjingUniversityofAeronautics&Astronautics,2006,23(3):161-167.

[10]郭剑东,宋彦国．小型无人倾转旋翼机全模式飞行操纵控制[J]．南京航空航天大学学报,2009,41(4):439-444.

[11]张达敏,张霄力．连续区间系统的鲁棒H∞控制:LMI方法[J]．厦门大学学报(自然科学版),2009,48(5):651-655.

[12]李忠建．大包线飞行控制系统鲁棒设计研究[D]．西安：西北工业大学,2000：36-37.

[13]熊治国,董新民．程序调参飞行控制规律的研究与展望[J]．飞行力学,2003,21(4):9-13

[14]俞立．鲁棒控制——线性矩阵不等式处理方法[M]．北京:清华大学出版社,2002:86-91.

Robust H∞Gain-scheduling Control for Mode Conversion of Tilt Rotor Aircrafts

CAI Xihai,FU Rong,ZENG Jianping*

(School of Aerospace Engineering,Xiamen University,Xiamen 361005,China)

Abstract:This paper is concerned with the flight control problem for small tilt rotor unmanned aerial vehicles (UAV) during conversion flights．Based on the robust H∞control,a gain scheduling method is given,and the design condition is in the form of linear matrix inequality (LMI)．Moreover,for the purpose of handling the control-redundancy problem,a set of practical allocation strategies is provided．Finally,aimed at the conversion flight control of the aircraft,a simulation is carried out on the longitudinal dynamical model．It shows that aircraft can complete the conversion-mode flight accurately along the predetermined trajectory,and the controller is not only robust to variations of the aerodynamic parameters,but also valid for the suppression of gust disturbances.

Key words:tilt rotor aircraft;control allocation;gain-scheduling;robust H∞control

doi：10.6043/j.issn.0438-0479.2016.03.014

收稿日期：2015-10-21录用日期：2015-11-20

基金项目：国家自然科学基金(61374037);中央高校基本科研业务费专项(20720150177)

*通信作者：jpzeng@xmu.edu.cn

中图分类号:V 249.1

文献标志码：A

文章编号：0438-0479(2016)03-0382-08

引文格式：蔡系海,付荣,曾建平.倾转旋翼机模态转换的鲁棒H∞增益调度控制.厦门大学学报(自然科学版)，2016,55(3)：382-389.

Citation：CAI X H,FU R,ZENG J P．Robust H∞gain-scheduling control for mode conversion of tilt rotor aircrafts.Journal of Xiamen University(Natural Science)，2016,55(3)：382-389．(in Chinese)