关于单模的顶点和核的一点注记

胡啸晗，杜　妮

(厦门大学数学科学学院，福建厦门361005)

关于单模的顶点和核的一点注记

胡啸晗，杜妮*

(厦门大学数学科学学院，福建厦门361005)

摘要：设G为有限群,k是特征为p的代数闭域(p>0).另设S是单kG-模,V(S)是S的一个顶点,Ker(S)是S的核.在本文中,若Op′(G)⊆Z(G)且每个属于主p-块的单kG-模S均有V(S)⊆Ker(S),则对每个x∈G,令Q=P∩Px,G中存在一个包含Op′(G)的正规子群H,满足Q∈Sylp(H)且|NH(Q)/Q|=|Op′(G)|.另外,设B为G的一个p-块,得到了B为p-根块的一个充分条件.

关键词：单模;顶点;核;p-根块

1背景和主要结论

在本文中,恒设G为有限群,k是特征为p的代数闭域(p>0),P是G的一个Sylowp-子群.另外,文中提及的模均为有限生成左模.

Motose等提出了p-根群的概念.若(kP)G是半单的,其中kP是平凡的kP-模,则称G是一个p-根群.为了研究p-根群与p-幂零群之间的关系,Tsushima提出了p-根块的概念.称G的一个p-块B为p-根块,若eB(kP)G是半单的,其中eB是对应B的块幂等元.在这两个概念提出之后,许多数学家对p-根群进行了深入研究,并取得了大量成果[1-4].特别地,Feit对p-根群进行了详细的介绍(见文献[5]的第6章第6节).

设S是单kG-模且P(S)={H≤G|S是kH-投射模}.称V(S)是S的一个顶点,若V(S)是子群集P(S)中的极小元(见文献[5]中第3章第4节).设Ker(S)={x∈G|xv=v,对任意v∈S}是S的核.在本文中,我们考虑如下条件:

V(S)⊆Ker(S).

(1)

Hida讨论了: 对每个单kG-模S,S均满足条件(1)的情形,并对群G给出了一个抽象群的刻画.

受文献[6]的启发,我们考虑: 对每个属于主p-块的单kG-模S,S均满足条件(1)的情形,并将文献[6]中结论推广到G的主p-块上,得到了如下结论.

定理1若G满足如下两个条件:

(i) Op′(G)⊆Z(G).

(ii) 对每个属于主p-块B0的单kG-模S,均有V(S)⊆Ker(S).

则对于每个x∈G,令Q=P∩Px,G 中存在一个包含Op′(G)的正规子群H,满足Q∈Sylp(H)并且|NH(Q)/Q|=|Op′(G)|.

在文献[3]中,Koshitani给出了G是p-根群的一个充分条件: 若每个单kG-模S均有SNG(Q)为单kNG(Q)-模,其中Q为S的一个顶点,则G是p-根群.我们将上述结果推广到p-块上,得到如下结论.

定理2设B为G的一个p-块.若每个属于B的单kG-模S,均有SNG(Q)为单kNG(Q)-模,其中Q为S的一个顶点,则B为p-根块.

本文未定义的记号和术语可参考文献[5].

2预备知识

为了方便读者,我们给出几个辅助性的引理.

引理1(文献,第四章引理4.12(iii)) 设B0是G的主p-块,则Op′,p(G)=∩S∈B0Ker(S).

引理2(文献[7〗,推论3.7;文献[8〗,引理2)若每个属于主p-块的单kG-模S,均有V(S)⊆Ker(S),则G是p-可解群.

引理4(文献[6〗,定理2.6)下列条件等价.

(i) 对每个单kG-模S,均有V(S)⊆Ker(S).

(ii) G是p-可解群并且对每个x∈G,G中存在一个正规子群H,使得P∩Px∈Sylp(H)且NH(P∩Px)=P∩Px.

引理5(文献[6〗定理2.7)若每个单kG-模S,均有V(S)⊆Ker(S),则G是p-可解群且成立：

(i) 若p为奇数,则G/Op(G)的p-长至多为1.

(ii) 若p=2,则G/O2(G)的2-长至多为2.

引理6(文献[4〗,定理)若每个属于p-块B的单kG-模S,均有V(S)⊆Ker(S),则B为p-根块.

引理7(文献[5〗,第3章推论2.13(i))设H是G的正规p-子群且S为单kG-模,则H⊆Ker(S).

引理8(文献[9〗,定理2.1)若G是p-可解群,则Op′(G)=1当且仅当kG只有一个p-块,即kG作为群环是不可分的.

引理9设G是p-可解群,令B0是G的主p-块,则B0≅k(G/Op′(G))且k(G/Op′(G))只有一个p-块.

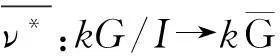
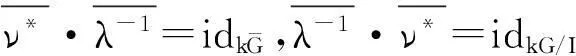
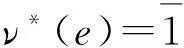
注1在引理9中,对B0≅k(G/Op′(G))的证明,我们采用了与文献[10]的第7章定理12.9及13.6不同的方法.

3主要结论的证明

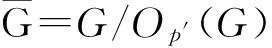
对每个x∈G,令Q=P∩Px,下面证明:G中存在一个包含Op′(G)的正规子群H,满足Q∈Sylp(H)且|NH(Q)/Q|=|Op′(G)|.

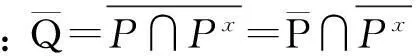
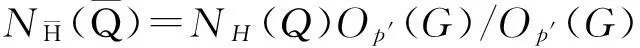
NH(Q)/NH(Q)∩Op′(G)≅Q.

因此,由于Op′(G)⊆Z(G),|NH(Q)/Q|=|NOp′(G)(Q)|=|Op′(G)|.

推论1若Op′(G)=1,则下列条件等价.

(i) 对每个属于主p-块的单kG-模S,均有V(S)⊆Ker(S).

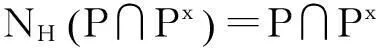
证明由于1=Op′(G)⊆Z(G),应用定理1及引理4,结论成立.

推论2若Op′(G)⊆Z(G)且每个属于主p-块的单kG-模S,均有V(S)⊆Ker(S),则G是p-可解群且下列结论成立.

(i) 若p为奇数,则G/Op′,p(G)的p-长至多为1.

(ii) 若p=2,则G/O2′,2(G)的2-长至多为2.

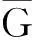
下面,我们给出一个例子来说明存在有限群G满足定理1的结论.

由定理2的证明可知,在主p-块上,定理2的条件比定理1的条件更强.因此,我们有如下推论.

推论3若G满足如下两个条件:

(i)Op′(G)⊆Z(G).

(ii) 每个属于主p-块B0的单kG-模S,均有SNG(Q)为单kNG(Q)-模,其中Q为S的一个顶点.

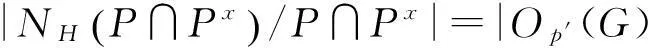
证明应用定理1及定理2的证明,即得结论.

参考文献：

[1]MOTOSE K,NINOMIYA Y.On the subgroupsHof a groupGsuch thatJ(KH)KG⊃J(KG)[J].Math J Okayama Univ,1975,17:171-176.

[2]TSUSHIMA Y.Onp-radical groups[J].J Algebra,1986,103:80-86.

[3]KOSHITANI S.A remark onp-radical groups[J].J Algebra,1990,134:491-496.

[4]HIDA A.Onp-radical blocks of finite groups[J].Proc Amer Math Soc,1992,114:37-38.

[5]FEIT W.The representation theory of finite groups[M].Amsterdam:North-Holland,1982:1-502.

[6]HIDA A.A note on kernels and vertices of simple modules[J].J Algebra,1995,171:917-920.

[7]KNÖRR R.On the vertices of irreducible modules[J].J Algebra,1979,86:487-499.

[8]HAMERNIK W,MICHLER G.On vertices of simple modules inp-solvable groups[J].Mitt Math Seminar Giessen,1976,121:147-162.

[9]FONG P,GASCHÜTZ W.A note on the modular representations of solvable groups[J].J Reine Angew Math,1961,208:73-78.

[10]HUPPERTB,BLACKBURNN.FinitegroupsII[M].Berlin:Springer-Verlag,1982：1-531.

A Note on Vertices and Kernels of Simple Modules

HU Xiaohan,DU Ni*

(School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)

Abstract:Let G be a finite group and k a field of characteristic p>0.And let S be a simple kG-module and V(S) a vertex of S.Also denote by Ker(S) the kernel of S.In this note,we give a group theoretical characterization of G if V(S)⊆Ker(S) for any simple kG-module S in the principal p-block of G.In addition,we obtain that a sufficient condition for p-radical blocks of G.

Key words:simple module;vertex;kernel;p-radical block

doi：10.6043/j.issn.0438-0479.2016.03.009

收稿日期：2015-10-19录用日期：2016-03-02

基金项目：国家自然科学基金(11201385)；福建省自然科学基金(2015J01027)；厦门大学校长基金(20720160003)

*通信作者：duni@xmu.edu.cn

中图分类号:O 152.6

文献标志码：A

文章编号：0438-0479(2016)03-0357-03

引文格式：胡啸晗，杜妮.关于单模的顶点和核的一点注记.厦门大学学报(自然科学版)，2016,55(3)：357-359.

Citation：HU X H,DU N．A note on vertices and kernels of simple modules.Journal of Xiamen University(Natural Science)，2016,55(3)：357-359．(in Chinese)