几乎导出匹配可扩图的一些度条件
2020-05-11杨田羽
杨田羽,王 勤
(1.中国计量大学 经济与管理学院,浙江 杭州 310018;2.中国计量大学 理学院,浙江 杭州 310018)
匹配问题在图论的相关研究中一直是一个热门问题,它不仅包含着一系列丰富的理论问题,还在实际应用中得到进一步的发展[1-2]。1980年,PLUMMER[3]提出了n-可扩图的概念,学者们围绕n-可扩图进行了大量的研究,并取得了一系列研究成果[4-6]。1998年,原晋江[7]提出了导出匹配可扩图的概念。自此,关于图的导出匹配可扩性和导出匹配可扩图的度条件的研究成果层出不穷,例如导出匹配可扩二部图的度条件[8],导出匹配可扩图和导出匹配可扩二部图的度和条件[9,10],结合图的导出匹配可扩性[11]以及极大导出匹配可扩图和极大非导出匹配可扩图的刻画,等等。杨帆等[12]研究了顶点数为2n的连通无爪图的导出匹配可扩性及其最小度条件为2┌-n/2┐+1。王勤等[13]研究了导出匹配可扩无爪图的度和条件。在此基础上,本文利用无爪图导出匹配的性质和几乎导出匹配可扩图的定义,进一步讨论几乎导出匹配可扩无爪图的一些度条件,并探讨二部图的几乎导出匹配可扩性。
1 准备工作
本文研究的图均为简单无向有限图。对于图G,我们分别用V(G)和E(G)来表示图G的顶点集和边集。对任一顶点u∈V(G),用
NG(u)={v∈V(G){u}|uv∈E(G)}
表示顶点u在图G中的邻集。将图G中连接顶点u的边的数目称为顶点u的度,记为dG(u),其中
δ(G)=min{dG(u)|u∈V(G)}
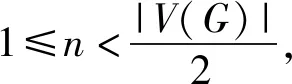
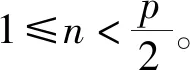
引理1.2[4]若G是一个有偶数个顶点的连通无爪图,则图G有完美匹配。
引理1.3[12]若M是无爪图G的一个导出匹配,则对任一顶点u∈V[G-V(M)],有|N(u)∩V(M)|≤4。
2 主要结果及其证明
定理2.1设图G是一个有2n-1个顶点的无爪图,若对图G中任意不相邻的顶点u和v,有
d(u)+d(v)≥2n+1,
(1)
则图G是几乎导出匹配可扩的。
证明取任意顶点x∉V(G),将x与G中的每个顶点连接,得到x与G的联图,记为G′=G∨{x}。欲证图G是几乎导出匹配可扩的,只需证明图G′是导出匹配可扩的。
已知图G中任意不相邻的顶点u和v满足度和条件(1),有
d(u)+d(v)≥2n+1。
而图G′=G∨{x}中,子图G的所有顶点均与x相连,则对图G′中任意不相邻的顶点u和v,有
d(u)+d(v)≥2n+3。
(2)
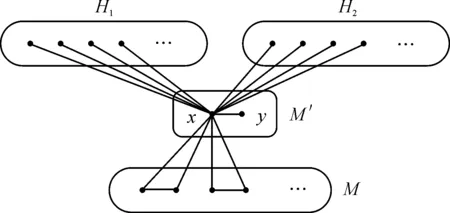
对满足1≤k 情形1M饱和顶点x 若M饱和顶点x,易知|M|=1。由于图G′是2-可扩的,则任一边数为1的导出匹配M可以扩充为G′的一个完美匹配(图1)。 图1 M饱和顶点xFigure 1 The vertex x is M-saturated 情形2M不饱和顶点x 若M不饱和顶点x,则假定存在一点y∈V[G-V(M)],将连接点x和点y的边看作一个匹配M′,且|V(M′)|=2,记H=G′-V(M)-V(M′)。 情形2.1H是连通的 此时,图H是一个有2n-|V(M)|-2个顶点的无爪图。由引理1.2可知,图H有完美匹配M″,从而M包含于G′的完美匹配M∪M′∪M″中(图2)。 图2 M不饱和顶点x且H是连通的Figure 2 The vertex x is M-unsaturated and H is connected 情形2.2H是不连通的 令H1和H2是H的两个分支,假设u∈V(H1),v∈V(H2)(图3)。 图3 M不饱和顶点x且H是不连通的Figure 3 The vertex x is M-unsaturated and H is disconnected 因为图G是无爪图,由引理1.3可知: |NG(u)∩V(M)|≤4, 即匹配M中分别有至多4个顶点与u,v相邻。则顶点u和顶点v在图G′中的度满足: dG′(u)≤|V(H1)|-1+4+|V(M′)| =|V(H1)|+5, dG′(v)≤|V(H2)|-1+4+|V(M′)| =|V(H2)|+5。 从而,顶点u和顶点v的度和满足 dG′(u)+dG′(v)≤|V(H1)|+|V(H2)|+10。 (3) 又因为 (4) 则根据式(2),(3),(4),有 2n+3≤dG′(u)+dG′(v) ≤|V(G′)|-|V(M)|-|V(M′)|+10 =2n+8-|V(M)|。 计算可得|V(M)|≤5,即|M|≤2。因为图G′是2-可扩的,所以匹配M可以扩充为图G′的一个完美匹配。 综上,图G′是导出匹配可扩的,从而图G是几乎导出匹配可扩的,定理2.1得证。 推论2.2设图G是一个有2n-1个顶点的无爪图,若图G的顶点的最小度满足 δ(G)≥n+1, (5) 则图G是几乎导出匹配可扩的。 证明已知图G中的顶点满足最小度条件(5),那么对于图G中任意不相邻的顶点u和v,有 d(u)≥n+1,d(v)≥n+1。 则图G中顶点u和顶点v的度和满足 d(u)+d(v)≥(n+1)+(n+1)=2n+2>2n+1。 由定理2.1可知,图G是几乎导出匹配可扩的。 定理2.3不存在几乎导出匹配可扩的二部图。 证明假设图G是一个有二部划分(A,B)的二部图,|A|+|B|=2n-1,且|A|<|B|。取任意顶点x∉V(G),将x与图G中的每个顶点连接,得到x与图G的联图,记为G′=G∨{x}。现将顶点x与任一顶点y∈A相连的边xy看作图G′的一个导出匹配M。记图H=G′-V(M)见图4)。 图4 二部图G与顶点x的联图G′Figure 4 The graph G′ obtained by joining vertex x to each vertex of G 因为|A|<|B|,所以|A|-1<|B|。易知,图H没有完美匹配。所以图G′不是导出匹配可扩的,因此不存在几乎导出匹配可扩的二部图G。 在本文中,我们通过研究图的完美匹配与几乎导出匹配可扩性的关系,得到了几乎导出匹配可扩无爪图的度和条件和最小度条件,并证明了不存在几乎导出匹配可扩的二部图。若图G是一个顶点数为2n-1的无爪图,我们证明了如果对图G中任意不相邻的顶点u和v,有d(u)+d(v)≥2n+1,那么图G是几乎导出匹配可扩的;并证明了如果图G的最小度δ(G)≥n+1,那么图G是几乎导出匹配可扩的。在后续的研究中,我们可以利用几乎导出匹配可扩图的性质,进一步研究相关极图的刻画,并探讨图的几乎导出匹配可扩性与图的连通性之间的关系。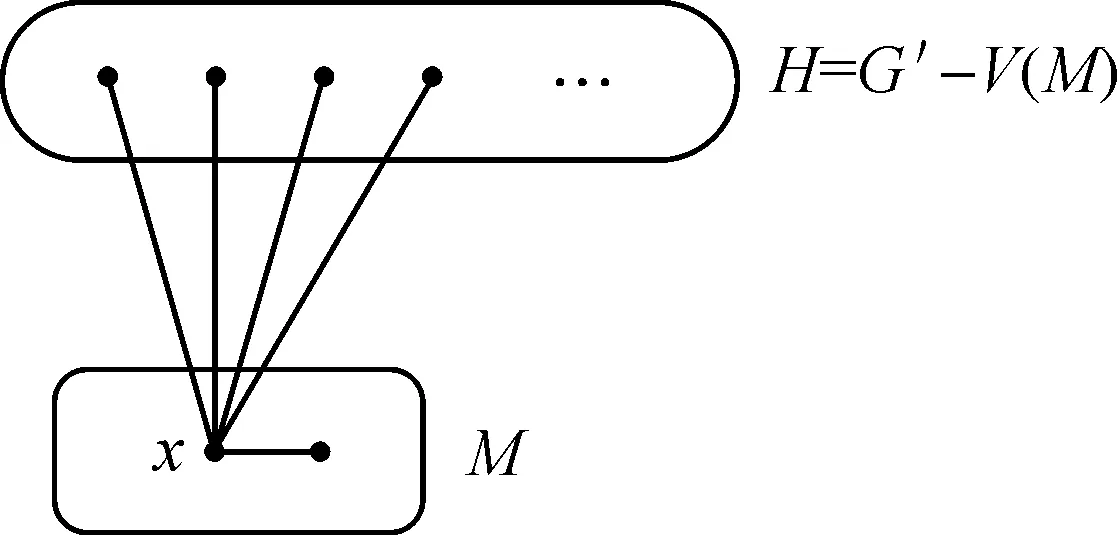
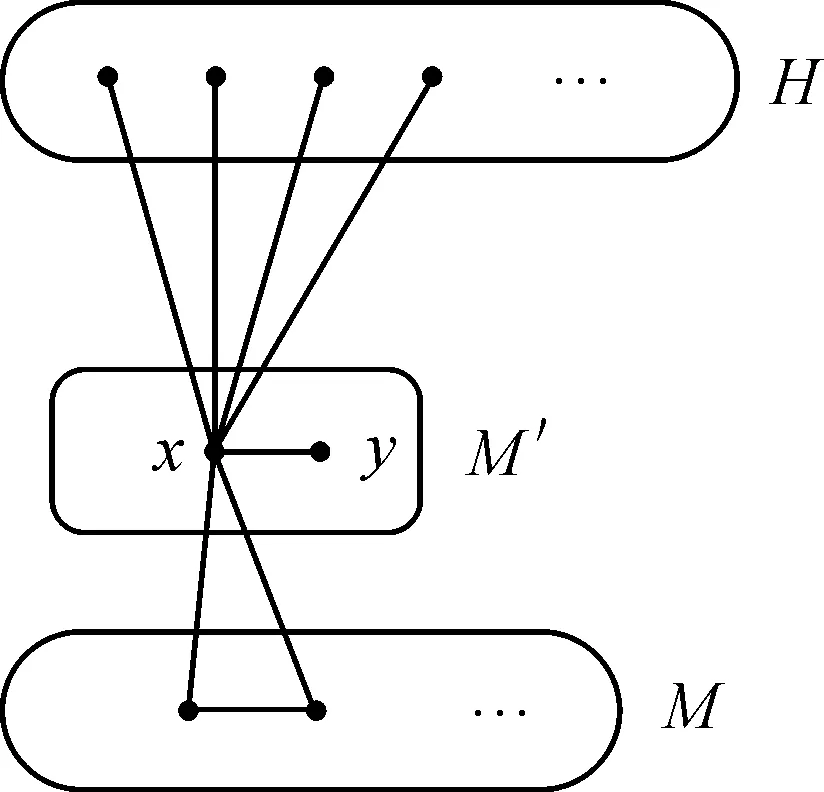
|NG(v)∩V(M)|≤4。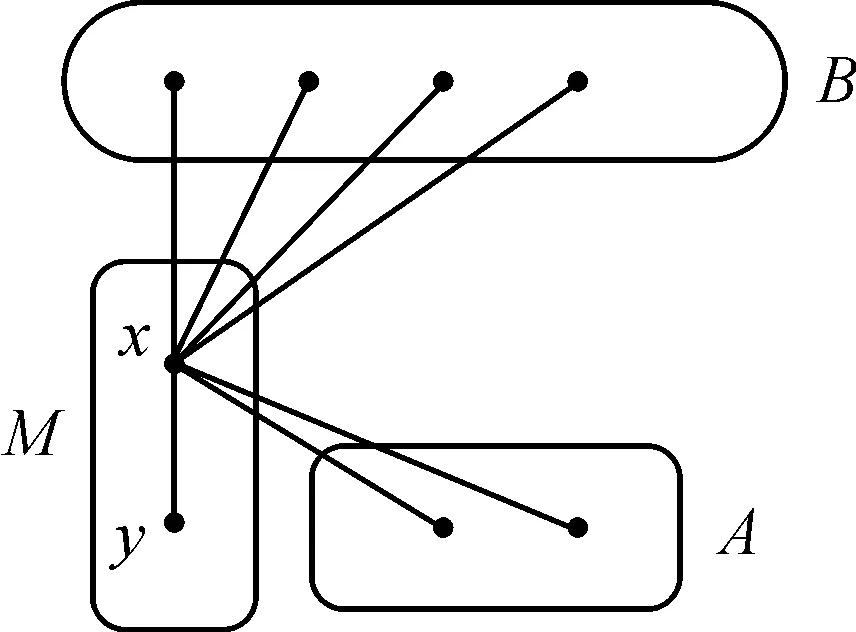
3 结 语
