多扇图的Pebbling数和Graham猜想

王艳秋, 叶永升

(淮北师范大学 数学科学学院，安徽 淮北 235000)



多扇图的Pebbling数和Graham猜想

王艳秋, 叶永升

(淮北师范大学 数学科学学院，安徽 淮北 235000)

图G的pebbling数f(G)是最小的整数n，使得不论n个pebble如何放置在G的顶点上，总可以通过一系列的pebbling移动把1个pebble移到任意一个顶点上，其中一个pebbling移动是从一个顶点处移走两个pebble而把其中的一个移到与其相邻的一个顶点上。Graham猜想对于任意的连通图G和H有f(G×H)≤f(G)f(H)。多扇图Fn1,n2,…,nm是指阶为n1+n2+…+nm+1的联图P1∨(Pn1∪Pn2∪…∪Pnm)。本文首先给出了多扇图的pebbling数，然后证明了多扇图Fn1,n2,…,nm具有2-pebbling性质，最后论述了对于一个多扇图和一个具有2-pebbling性质的图的乘积来说，Graham猜想是成立的。作为一个推论，当G和H都是多扇图时，Graham猜想成立。

运筹学；pebbling数；Graham猜想；pebbling移动；多扇图

0 引言

连通图的一个pebbling是一些pebble在这个图的顶点上的一种放置方式， 一个pebbling移动是从一个顶点上移走两个pebble。扔掉其中的一个而把另一个移到与其相邻的一个顶点上。图G的一个顶点v的pebbling数是最小的数f(G,v)满足从G的顶点上f(G,v)个pebble的任意一种放置开始， 总可以通过一系列的pebbling移动把一个pebble移到顶点v上。 图G的pebbling数记为f(G)，是对G的所有顶点v来说f(G,v)的最大值。

对于pebbling数f(G)已经得到了一些结果(见文献[1～5])，如果除顶点v之外每一个顶点上都只放置一个pebble，则没有一个pebble能够移到v上，另外，如果顶点w与v的距离为d，且2d-1个pebble放置在w上，则也不能把一个pebble移到v上，所以有f(G)≥max{|V(G)|,2d}。这里|V(G)|表示图G的顶点个数，而d为图G的直径。进一步地，从文献[1]知道f(Kn)=n·f(Pn)=2n-1，其中Kn为n个顶点的完全图，而Pn为n个顶点的路。

给定G的一种pebbling，设q为具有至少1个pebble的顶点个数，r为具有奇数个pebble的顶点个数，称G满足2-pebbling性质(或弱2-pebbling性质)， 如果当开始时总的pebble个数为2f(G)-q+1(或2f(G)-r+1)时，总可以把两个pebble移到某个特定的目标顶点上，满足2-pebbling性质的图也满足弱2-pebbling性质。给定G的一种pebbling，G的一个传送子图是一条路x0,x1…xk，使得在顶点x0上至少有两个pebble， 且除了可能xk外的其他顶点上至少有1个pebble。这时可以把1个pebble从x0传送到xk。

下面我们给出多扇图的定义。

联图G1∨G2[2]是指从并图G1∪G2中连接图G1的每个顶点和的G2每个顶点所得到的图。设Pn为n个顶点的路，称联图P1∨Pn为n+1阶的扇形图，记为Fn。 称联图P1∨(Pn1∪Pn2∪…∪Pnm)为n1+n2+…+nm+1阶多扇图，记为Fn1,n2,…,nm。 如图1所示。

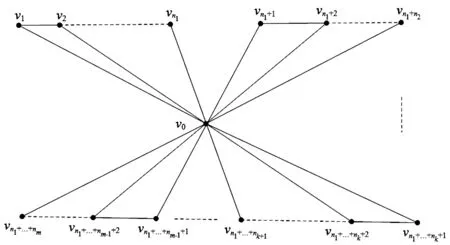
图1 多扇图Fn1,n2,…,nm

Graham猜想指出对任意的连通图G和H有f(G×H)≤f(G)f(H)。现已在很少的几种情形下验证了Graham猜想，其中有1棵树乘以1棵树[3]，一个圈乘以一个圈[1]，一个完全图乘以一个满足2-pebbling性质的图[1]，一个完全二部图乘以1个满足2-pebbling性质的图[4]，一个扇图乘以一个扇图[5]，而且我们已经知道了扇图的pebbling数，以及扇图满足2-pebbling性质，由此，本文给出了多扇图的pebbling数，并证明了多扇图满足2-pebbling性质，最后推导了一个多扇图乘以一个具有2-pebbling性质的图满足Graham猜想，由此可知两个多扇图的乘积也满足Graham猜想。

在本文中，G表示一个简单图，其顶点集为V(G)，边集为E(G)，对G的任意顶点v。P(v)代表v上的pebble的个数。

1 Fn1,n2,…,nm的pebbling数及其2-pebbling性质

在这一部分，我们首先给出Fn1,n2,…,nm的pebbling数，再证明Fn1,n2,…,nm具有2-pebbling性质。

定理1f(Fn1,n2,…,nm)=n1+n2+…+nm+2。

证明 我们把n1+n2+…+nm+1个pebble放在多扇图Fn1,n2,…,nm上，如果p(v0)=0，p(vn1+n2+…+nm)=3，p(v2)=p(v3)=…=p(vn1)=…=p(vn1+n2+…+nm-1)=1，那么目标顶点v1无法得到1个pebble，故F(Fn1,n2,…,nm)≥n1+n2+…+nm+2。下面证明f(Fn1,n2,…,nm)≤n1+n2+…+nm+2。

首先，设目标顶点为v0，即p(v0)=0，则一定存在某个i≥1，使得p(vi)≥2。所以可以从vi处移1个pebble给v0。

其次，设目标顶点为vk，即p(vk)=0，k∈{1,2,…,n1+n2+…+nm}。若p(v0)≥2或p(vi)≥4(i≥1且i≠k)，则{v0,vk}或{vi,v0,vk}构成一传送子图。所以vk可得到1个pebble。否则，p(v0)≤1且p(vi)≤3(i≥1且i≠k)。

(1)当p(v0)=1时，一定存在一个顶点v1，使得P(v1)≥2(i≥1且i≠k)，此时{vi,vo,vk}构成一传送子图。vk可得到1个pebble。

(2)当p(v0)=0时，n1+n2+…+nm-1个顶点上被放置n1+n2+…+nm+2个pebble，故在除去顶点v0,vk之外的顶点中，至少有2个顶点满足2≤p(vi),p(vj)≤3。则vi,vj分别可给v01个pebble，v0获得2个pebble后可移1个pebble给vk。

综上可知，f(Fn1,n2,…,nm)=n1+n2+…+nm+2。证毕

定理2 多扇图Fn1,n2,…,nm满足2-pebbling性质。

证明 记p为多扇图Fn1,n2,…,nm上的pebble个数，q为具有至少1个pebble的顶点个数，r为具有奇数个pebble的顶点个数，且p+q=2(n1+n2+…+nm+2)+1。设目标顶点为vi。若p(vi)=1，则除vi外，其余顶点的pebble个数为

2(n1+n2+…+nm+2)+1-q-1

≥2(n1+n2+…+nm+2)-(n1+n2+…+nm+1)

=n1+n2+…+nm+3>n1+n2+…+nm+2,

因为f(Fn1,n2,…,nm)=n1+n2+…+nm+2，利用这2(n1+n2+…+nm+2)+1-q-1个pebble，可以再往vi上放1个pebble。如果p(vi)=0，则考虑以下情形：

(1)i=0，即目标顶点为v0，而q+r≤2(n1+n2+…+nm)，则

p-r=2(n1+n2+…+nm+2)+1-q-r

≥2(n1+n2+…+nm+2)+1-2(n1+n2+…+nm)=5

从而至少可以从顶点v1,v2,…,vn1+n2+…+nm上移2个pebble到v0上。

(2)i≠0，不失一般性，设目标顶点为v1，即p(v1)=0，

1)如果p(v0)≥4， 那么可以利用v0上4个pebble移2个到v1上。

2)如果2≤p(v0)≤3， 那么可以从v0移1个pebble到v1上， 另外除v0和v1外， 其余顶点的pebble个数为

2(n1+n2+…+nm+2)+1-q-p(v0)≥2(n1+n2+…+nm+2)+1-(n1+n2+…+nm)-3

=n1+n2+…+nm+2=f(Fn1,n2,…,nm)

于是可以利用这2(n1+n2+…+nm+2)+1-q-p(v0)个pebble再往v1上放1个pebble。

3)如果p(v0)=1，那么q+r≤2(n1+n2+…+nm)，除v0和v1外，其余顶点的pebble个数为p-1，具有奇数个pebble的顶点个数为r-1，于是(p-1)-(r-1)=p-r=2(n1+n2+…+nm+2)+1-q-r≥5，由于p-r不可能为奇数，所以p-r≥6。从而至少可移3个pebble到v0，这时利用v0上的4个pebble移2个给v1。

4)如果p(v0)=0，那么q+r≤2(n1+n2+…+nm-1)，于是p-r=2(n1+n2+…+nm+2)+1-q-r≥7，所以p-r≥8，从而至少可移4个pebble到v0，再从v0移2个到v1上。证毕

2 Fn1,n2,…,nm的Graham猜想

设G和H为两个图，G和H的Descartes积G×H是一个图，其顶点集为Descartes积V(G×H)=V(G)×V(H)={(x,y)|x∈V(G),y∈V(H)}，且两个顶点(x,y)与(x′,y′)相邻当且仅当x=x′，且{y,y′}∈E(H)，或者{x,x′}∈E(G)且y=y′。可以用图形来表示出G×H，即在G的每一个顶点处画出一个H的图形，并且把任一H中的每一个顶点和与此H相邻的H中的对应顶点连接起来。用{x}×H(或G×{y})来表示顶点投射到V(G)上为顶点x(或投射到V(H)上为顶点y)的G×H的子图。

首先给出三个引理，然后证明对于一个多扇图和一个具有2-pebbling性质的图的乘积来说，Graham猜想成立。

引理1[1]如果G′是G的一个生成子图，则f(G′)≥f(G)。

引理2[6]设K1,n为一个星形图，则当n>1时，有f(K1,n)=n+2。

引理3[6]设G满足2-pebbling性质，则f(K1,n×G)≤f(K1,n)f(G)。

定理3 设G满足2-pebbling性质，则f(Fn1,n2,…,nm×G)≤f(Fn1,n2,…,nm)f(G)。

证明 由引理1，可知f(Fn1,n2,…,nm×G)≤f(K1,n1+n2+…+nm×G)。 由引理2和引理3，可得到f(K1,n1+n2+…+nm×G)≤(n1+n2+…+nm+2)f(G)。因此，我们有f(Fn1,n2,…,nm×G)≤f(Fn1,n2,…,nm)f(G)。证毕

由多扇图满足2-pebbling性质，可得下面的推论：

推论f(Fn1,n2,…,nm×Fs1,s2,…,st)≤(n1+n2+…+nm+2)(s1+s2+…+st+2)。

[1] Chung F R K. Pebbling in hypercubes[J]. SIAMJ. Discrete Math, 1989, 2(4): 467- 472.

[2] 王力工等,多扇图中保Wiener指数的树[J].湖南师范大学自然科学学报,2012,35(1):17-18.

[3] Moews D. Pebbling graphs[J]. Combin Theory(Series B), 1992, 55: 244-252.

[4] 冯荣权,金珠英.完全二部图乘积上的Graham pebbling猜想[J].中国数学(A辑),2001,31(3):199-203.

[5] FENG R Q, KIM J Y. Pebbling numbers of some graphs[J]. Science in China(Series A), 2002; 45(4): 470- 478.

[6] 胡蔚勇.星形图乘积上的Graham pebbling猜想[J].无锡商业职业技术学院学报,2003,3(2):68-70.

The Pebbling Number of Multi-fan Graphs and Graham’s Conjecture

WANG Yan-qiu YE Yong-sheng

(CollegeofMathematicalScience,HuaibeiNormalUniversity,Huaibei235000,China)

The pebbling number of a graphG,f(G) , is the leastn, no matter hownpebbles are placed on the vertices ofG, a pebble can be moved to any vertex by a sequence of pebbling moves. A pebbling move consists of the removal of two pebbles vertex and the placement of one of those two pebbles on an adjacent vertex. Graham conjectured that for any connected graphsGandH,f(G×H)≤f(G)f(H) . Multi-fan graphFn1,n2,…,nmis a joint-graphP1∨(Pn1∪Pn2∪…∪Pnm) withn1+n2+…+nm+1 vertices. This paper shows thatf(Fn1,n2,…,nm)=n1+n2+…+nm+2 andFn1,n2,…,nmwith the 2-pebbling property. Graham’s conjecture holds of a multi-fan graphs by a graph with the 2-pebbling property. As a corollary, Graham’s conjecture holds when G and H are multi-fan graphs.

operational research; pebbling number; Graham’s conjecture; pebbling move; multi-fan graphs

2013-12-28

安徽省自然科学基金资助项目(1408085MA08; KJ2013Z279)

王艳秋(1989-)，女，安徽淮北人，硕士生，研究方向：图论及其应用；叶永升(1964-)，男，安徽嘉山人，教授，硕士生导师，研究方向：图论及其应用。

O157.5

A

1007-3221(2015)04- 0137- 04