完全二部图K9,n(9≤n≤92)的点可区别E-全染色

杨伟光, 陈祥恩

(西北师范大学 数学与统计学院, 兰州 730070)

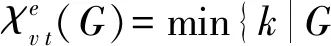
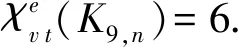
证明: 先证K9,n不存在5-VDET染色. 假设K9,n有1个5-VDET染色f, 所用颜色为1,2,3,4,5, 则需考虑以下4种情形.

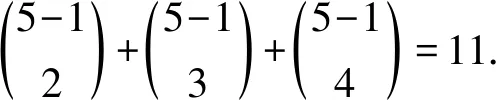
当9≤n≤11时, A1中的2-子集至多有2个不是Y中顶点的色集合, 因此, 在2,3,4,5中至少有2种色包含在每个C(ui)中, 不妨设2,3∈C(ui)(i=1,2,…,9), 则每个C(ui)只能是以下集合之一: {1,2,3},{1,2,3,4},{1,2,3,5},{1,2,3,4,5}, 4个集合不能区分X中的9个顶点, 矛盾.

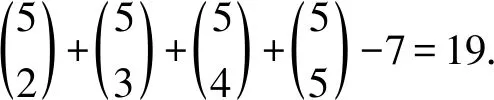
分两种子情形讨论:

① B2中至少有一个子集是Y中顶点的色集合, 不妨设为{1,2,3}. 由{1,2,3}是Y中顶点的色集合, 可得1,2∈C(ui)(i=1,2,…,9), 则每个C(ui)只能是下面集合之一: {1,2},{1,2,3},{1,2,4},{1,2,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,2,3,4,5}, 共8个集合, 矛盾.

② B2中的子集均不是Y中顶点色集合. 下面仅考虑当9≤n≤16时的情形. 此时, 在B2∪B3中至多有7个集合不是Y中顶点色集合.

(i) B1中至少有一个集合是Y中顶点色集合. 不妨设{3,4}是Y中顶点色集合, 可得3∈C(ui)(i=1,2,…,9)或4∈C(ui)(i=1,2,…,9). 不妨设前者成立, 故{1,2},{1,4},{1,5},{2,4},{2,5},{1,2,4},{1,2,5}不是任意点的色集合, 从而

若{1,2,3}不是任意点的色集合, 则B1中的集合均为Y中顶点色集合, 从而在3,4,5中至少有2种色包含在每个C(ui)中, 不妨设 3,4∈C(ui)(i=1,2,…,9), 则每个C(ui)只能是以下集合之一: {1,3,4},{1,3,4,5},{2,3,4},{2,3,4,5},{1,2,3,4},{1,2,3,4,5}, 6个集合不能区分X中的9个顶点, 矛盾. 若{4,5}不是任意点的色集合, 则{1,2,3}是X中顶点的色集合, 又{1,4,5}和{2,4,5}是X中顶点的色集合, 且由假设{3,4}是Y中顶点色集合, 故矛盾.

(ii) B1中集合都不是Y中顶点色集合. 此时B3中至多有4个集合不是Y中顶点色集合， 则{1,2}不是任意点的色集合, 故{1,3},{1,4},{1,5}均不是X中任意点的色集合, 或{2,3},{2,4},{2,5}均不是X任意点的色集合. 否则, {1,3},{2,4}是X顶点的色集合, 则3,4∈C(vj). 故{1,3},{2,3}均不是X中点的色集合； {1,4},{2,4}均不是X中点的色集合； {1,5},{2,5}均不是X中点的色集合. 这3个结论至少有两个是正确的. 假设最多有一个是正确的, 不妨设后两个错误, 则{1,4},{2,5}是X任意点的色集合, 从而4,5∈C(vj), 又B3中同时含4,5的只有7个, 不能区分n个顶点, 矛盾. 不妨设前两个结论正确, 则{1,3},{2,3},{1,4},{2,4}均不是任意点的色集合, 从而{3,4},{3,5},{4,5},{1,2}也均不是任意点的色集合, 由于26-8=18, 只能n=9. 若{1,5},{2,5}是X任意点的色集合, 则{2,5}∩{1,3,4}≠Ø, 故剩下的集合不能区分K9,9中的18个顶点, 矛盾.

分以下两种子情形讨论.

① {4,5}是Y中顶点色集合, 可得4∈C(ui)(i=1,2,…,9)或5∈C(ui)(i=1,2,…,9), 不妨设前者成立. 若{1,4},{2,4},{3,4}中至少有一个是X某个点的色集合, 则每个C(vj)都包含4, 故{1,2,5},{1,3,5},{2,3,5},{1,2,3,5}不是任意点的色集合, 因此C(X)∪C(Y)⊆∪C{{1,4},{2,4},{3,4}}, 且不包含{1,2,5},{1,3,5},{2,3,5},{1,2,3,5}, 有9+n≤16+3-4, 可得n≤15, 故15个集合不能区分X和Y中(9+n)个顶点, 矛盾. 若{1,4},{2,4},{3,4}都不是X中点的色集合, 则C(X)∪C(Y)⊆C, 只能n=9, 从而{1,2,5},{1,3,5},{2,3,5},{1,2,3,5}是Y中点的色集合, 故1,2,3∈C(ui)(i=1,2,…,9), 可得每个C(ui)只能是下面集合之一: {1,2,3,4},{1,2,3,4,5}, 矛盾.

② {4,5}不是Y中顶点色集合时, 显然也不是X中任意点色集合, 则C(Y)⊆C2∪C3.

事实1以下3个结论最多有一个是正确的：

(i) {1,2},{1,3},{2,3}中至少有一个是X中某个顶点的色集合；

(ii) {1,4},{2,4},{3,4}中至少有一个是X中某个顶点的色集合；

(iii) {1,5},{2,5},{3,5}中至少有一个是X中某个顶点的色集合.

当结论(i),(ii)正确时,Y中每个点的色集合同时包含1,4(或2,4或3,4), 但C2∪C3中同时包含1,4的只有7个集合, 矛盾； 当结论(ii),(iii) 正确时,Y中每个点的色集合同时包含4,5(或2,4或3,4), 但C2∪C3中同时包含4,5的只有7个集合, 矛盾； 当结论(i),(iii)正确时, 类似于当结论(i),(ii)正确的情形, 矛盾.

事实2事实1中3个结论都不正确.

设结论(i)正确, 则Y中每个点的色集合同时包含1,2,3中的某一色, 不妨设为1, 则可作为Y中顶点的色集合有10个, 且{1,4},{2,4},{3,4},{1,5},{2,5},{3,5},{4,5}均不是任意点的色集合, 从而在{1,2,4},{1,2,5},{1,3,4},{1,3,5}中至少有3个都是Y中点的色集合, 不妨设前3个是Y中点的色集合, 则可得每个C(ui)同时包含1,2和1,3或1,2,3(i=1,2,…,9), 又可作为Y中顶点的色集合的10个集合中最多有一个不是Y中点的色集合, 记为A, 故每个C(ui)只能是以下集合之一： {1,2},{1,3},{1,2,3},{A}, 矛盾. 设结论(ii)正确, 则Y中每个点的色集合同时包含4, 故{1,2},{1,3},{2,3},{1,5},{2,5},{3,5},{4,5}不是任意点的色集合, 即9+n≤3+10+5, 可得n≤10, 故C(Y)⊆{{1,2,4},{1,3,4},{2,3,4},{1,4,5},{2,4,5},{3,4,5},{1,2,3,4},{1,2,4,5},{1,3,4,5},{2,3,4,5},{1,2,3,4,5}}, 由于{1,4}是X中某顶点的色集合, 因此{1,2,4},{1,3,4},{2,3,4}不是Y中点的色集合, 即11-3=8, 8个集合不能区分Y中n个顶点, 矛盾. 当结论(iii)正确时, 可类似得矛盾.

由事实1和事实2可知,C(X)∪C(Y)⊆C2∪C3∪{{1,2,3}}, 即9+n≤9+6+1, 可得n≤7, 矛盾.

表1 K9,32的6-VDET染色f32

注：A1={1,3,4,5}，A2={2,3,4,5}，A3={1,3,4,6}，A4={2,3,4,6}，A5={1,3,4,5,6}，A6={2,3,4,5,6}，A7={1,2,3,4,5}，A8={1,2,3,4,6}，A9={1,2,3,4,5,6}.

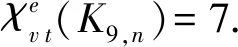
证明: 先证K9,n不存在6-VDET染色. 假设K9,n有1个6-VDET染色f, 所用颜色为1,2,3,4,5,6, 则需考虑以下5种情形.

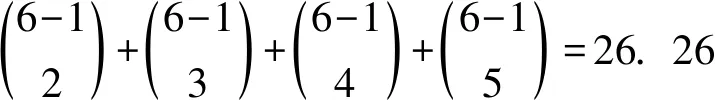
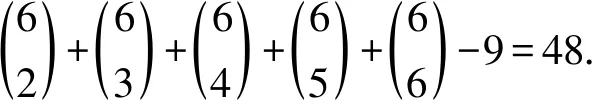
注意到在B中包含i的集合有26个,i=1,2; 在B中包含j的集合有29个,j=3,4,5,6. 因此, 每个C(vj)至少包含3种颜色, 故C(X)⊆B2∪B3,C(X)∪C(Y)⊆B, 有9+n≤48, 可得n≤39. 从而当40≤n≤48时, B中的集合不能区分X和Y中的(9+n)个顶点, 矛盾. 下面仅考虑当33≤n≤39时的情形.

① B2中至少有一个集合是Y中顶点的色集合. 此时1,2∈C(ui)(i=1,2,…,9). 因此B1中的集合均不是Y中顶点色集合, 否则, 若B1中有一个集合是Y中顶点色集合, 可得3,4,5,6中至少有一种色包含在每个C(ui)中, 不妨设3∈C(ui)(i=1,2,…,9). 从而1,2,3∈C(ui)(i=1,2,…,9), 因此每个C(ui)只能是以下集合之一: {1,2,3},{1,2,3,4},{1,2,3,5},{1,2,3,6},{1,2,3,4,5},{1,2,3,4,6},{1,2,3,5,6},{1,2,3,4,5,6}, 8个集合不能区分X中的9个顶点, 矛盾. 故当33≤n≤39时, B2和B3中的集合不能区分X和Y中的(9+n)个顶点, 矛盾. 由于B1中的集合均不是X和Y中任意点的色集合, 且42≤9+n≤48, 因此当43≤9+n≤48时, 42个集合不能区分Y中的(9+n)个顶点, 矛盾. 下面仅考虑9+n=42, 即n=33时的情形.

(i) {1,2,3},{1,2,4},{1,2,5},{1,2,6}中至少有一个是X中点的色集合. 由于{4,5,6}为Y中顶点色集合, 且{1,2,3}∩{3,4,5}=Ø, 故42个集合不能区分X和Y中的(9+n)个顶点, 矛盾.

(ii) B2中的集合均不是X中任意点的色集合, 则均为Y中顶点的色集合, 又{3,4,5},{3,4,6},{4,5,6},{3,4,5,6}为Y中顶点色集合, 故每个C(ui)至少同时包含3,4,5,6中的某两种色, 从而每个C(ui)只能是以下集合之一: {1,2,3,4},{1,2,3,5},{1,2,3,6},{1,2,4,5},{1,2,4,6},{1,2,5,6},{1,2,3,4,5},{1,2,3,4,6},{1,2,3,5,6},{1,2,4,5,6},{1,2,3,4,5,6}. 不妨设C(u1)={1,2,3,4},f(u1)=1, 由于{1,5,6},{2,5,6}为Y中顶点色集合, 且不能同时正常染色, 矛盾； 当C(X)中某点的色集合是{1,2,3,5},{1,2,3,6}时, 同理也可得出矛盾. 即{1,2,3,4},{1,2,3,5},{1,2,3,6}不能作为X中任意点的色集合, 剩下8个集合不能区分X中的9个顶点, 矛盾.

② B2中的集合都不是Y中顶点色集合.

(i) B2中至少有一个集合是X中顶点色集合. 不妨设C(ui0)={1,2,3},f(ui0)=1, 则每个C(vj)包含颜色2或3, 故{4,5},{4,6},{5,6},{1,4,5},{1,4,6},{1,5,6},{4,5,6},{1,4,5,6}均不是Y中顶点色集合. 若{1,4,5},{1,4,6},{1,5,6},{1,4,5,6}中至少有一个是X中顶点色集合, 不妨设C(ui1)={1,4,5},f(ui1)=1, 则每个C(vj) 包含颜色4或5, 故{3,4},{3,5},{3,6},{1,3,4},{1,3,5},{1,3,6}均不是Y中顶点色集合, 因此n≤48-8-6-4, 即n≤30, 矛盾； 若{1,4,5},{1,4,6},{1,5,6},{1,4,5,6}均不是X中顶点色集合, 则 9+n≤48-8, 即n≤31, 矛盾.

(ii) B2中的集合都不是X中顶点色集合. 此时C(X)∪C(Y)⊆B1∪B3, 有9+n≤6+38,n≤33. 故下面仅考虑n=33时的情形. 此时B1中的集合全为Y中顶点色集合. 3,4,5,6中至少有3种色同时包含在每个C(ui)中, 不妨设3,4,5∈C(ui)(i=1,2,…，9), 则每个C(ui)只能是以下集合之一: {1,3,4,5},{2,3,4,5},{1,3,4,5,6},{2,3,4,5,6},{1,2,3,4,5},{1,2,3,4,5,6}, 矛盾.

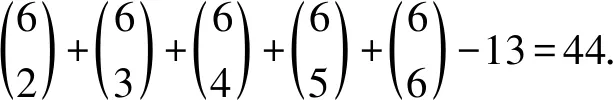
注意到C中包含25个i集合(i=1,2,3), 包含28个j集合(i=4,5,6), 因此每个C(ui)至少包含3种色, 故C(X)⊆C2∪C3∪{{1,2,3}},C(X)∪C(Y)⊆C∪{{1,2,3}}, 有9+n≤44+1, 可得n≤36. 从而当37≤n≤92时, 45个集合不能区分X和Y中的(9+n)个顶点, 矛盾. 下面仅考虑33≤n≤36时的情形.

① {1,2,3}是X中顶点色集合， 则{4,5},{4,6},{5,6},{4,5,6}均不是X和Y中任意顶点色集合,C(X)∪C(Y)⊆{{1,2,3}}∪C2∪C3{{4,5,6}}, 有9+n≤1+9+32-1, 可得n≤32. 矛盾.

② {1,2,3}不是X中顶点色集合, 此时C(X)⊆C2∪C3,C(X)∪C(Y)⊆C, 有9+n≤44, 可得n≤35. 故下面仅考虑33≤n≤35时的情形.

(i) C1中的集合都是Y中顶点色集合. 此时4,5,6中至少有2种色同时包含在每个C(ui)中, 不妨设4,5∈C(ui)(i=1,2,…,9), 则C2中的集合都不是X中顶点色集合, 此时C(X)⊆C3, 且C2中至多有两个不是Y中顶点色集合, 因此1,2,3∈C(ui)(i=1,2,…,9), 则每个C(ui)只能是以下集合之一: {1,2,3,4,5},{1,2,3,4,5,6}, 矛盾.

(ii) C1中的集合恰有一个不是Y中顶点色集合, 也不是X中顶点色集合. 此时4,5,6中至少有1种色同时包含在每个C(ui)中, 不妨设4∈C(ui)(i=1,2,…,9), 则{1,2,5},{1,2,6},{1,3,5},{1,3,6},{2,3,5},{2,3,6}均不是X中顶点色集合. 由于{1,2,5},{1,2,6},{1,3,5},{1,3,6},{2,3,5},{2,3,6}均为Y中顶点色集合及至多有一个不是Y中顶点色集合, 均可得1,2,3∈C(ui)(i=1,2,…,9), 则每个C(ui)只能是以下4个集合之一: {1,2,3,4,5,6},{1,2,3,4},{1,2,3,4,5},{1,2,3,4,6}, 矛盾.

(iii) C1中的集合恰有2个不是Y中顶点色集合. 此时4,5,6中至少有1种色同时包含在每个C(ui)中, 不妨设4∈C(ui)(i=1,2,…,9), 则{1,2,5},{1,2,6},{1,3,5},{1,3,6},{2,3,5},{2,3,6}均不是X中顶点色集合, 且全为Y中顶点色集合. 可得1,2,3∈C(ui)(i=1,2,…,9), 则每个C(ui)只能是以下4个集合之一: {1,2,3,4,5,6},{1,2,3,4},{1,2,3,4,5},{1,2,3,4,6}, 矛盾.

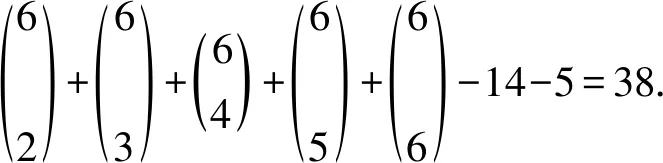
注意到D中包含22个i集合(i=1,2,3,4), 包含27个j集合(i=5,6). 因此每个C(ui)至少包含3种色, 故C(X)⊆D2∪D3∪{{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}},C(X)∪C(Y)⊆D∪{{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}}, 有9+n≤38+5, 可得n≤34. 从而当35≤n≤38时, 43个集合不能区分X和Y中的(9+n)个顶点, 矛盾. 下面仅考虑33≤n≤34时的情形.

① {5,6}是Y中某顶点v(j0)的色集合. 此时5∈C(ui)或6∈C(ui)(i=1,2,…，9), 不妨设前者成立. 则{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}均不是X中顶点色集合, 故C(X)∪C(Y)⊆D, 即9+n≤38, 可得n≤29, 29个集合不能区分Y中的n个顶点, 矛盾.

② {5,6}不是Y中任一顶点的色集合. 则{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}均是X中顶点色集合, 设C(ui0)={1,2,3},f(ui0)=1, 则每个C(vj)包含颜色2或 3, 故{1,4,5},{1,4,6},{1,5,6},{4,5,6},{1,4,5,6}不是Y中顶点色集合, 由于38-1-5=32, 32个集合不能区分Y中的n个顶点, 矛盾.

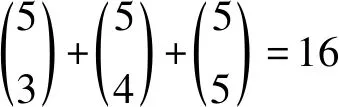
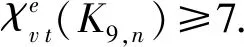
首先确定f92, 令由X∪{v1,v2,…,v32}所导出的K9,92的子图按表1列出的6-VDET染色f32进行染色; 然后染其他的顶点和关联边. 令vj(33≤j≤45)及其关联边按表2所列方案进行染色.

表2 当33≤j≤45时K9,92的顶点vj及其关联边的染色方案

注：B1={2,3,4,5,6,7}，B2={1,3,4,5,6,7}，B3={1,2,3,4,6,7}，B4={1,2,3,4,5,7}，B5={2,3,4,6,7}，B6={2,3,4,5,7}，B7={1,3,4,6,7}，B8={1,3,4,5,7}，B9={1,2,3,4,5,6,7}.

令顶点v46,v47,…,v92分别对应下列集合: 含颜色7的3-子集、 4-子集、 5-子集、 6-子集, 但不是{1,2,7},{2,3,4,5,6,7},{1,3,4,5,6,7},{1,2,3,4,6,7},{1,2,3,4,5,7},{2,3,4,6,7},{2,3,4,5,7},{1,3,4,6,7},{1,3,4,5,7},{1,2,3,4,5,6,7}中的任意一个集合. 顶点vj(46≤j≤92)及其关联边的染色方案列于表3. 当33≤j≤91时,K9,92的7-VDET染色f92在由X∪{v1,v2,…,vj}所导出的子图上的限制是K9,j的7-VDET染色fj.

表3 当46≤j≤92时K9,92的顶点vj及其关联边的染色方案