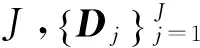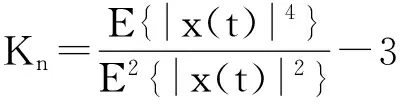应用奇异值分解和峭度分离滚动轴承复合故障

王　宇，钟　雯，尹　洋，宋春华，童　俊

(西华大学机械工程学院,四川 成都　610039)



应用奇异值分解和峭度分离滚动轴承复合故障

王宇，钟雯，尹洋，宋春华，童俊

(西华大学机械工程学院,四川 成都610039)

摘要：滚动轴承多故障特征影响故障诊断结果，为此提出一种结合奇异值分解和峭度的复合故障诊断方法。将采集的双通道多故障特征振动信号进行多层奇异值分解，利用奇异值差分谱和归一化峭度进行筛选和重构，实现对多故障特征的分别提取；通过滚动轴承内外圈故障实验，最终分离出轴承的2种故障。与直接采用原始信号诊断相比，该方法能够在背景噪声下准确分离频率相近的微弱故障成分，提高提取瞬态冲击信号特征的能力，能有效识别滚动轴承的故障类型和发生部位，提高复合故障诊断的准确性。实验结果表明，该方法可以有效地分离和提取滚动轴承多故障特征。

关键词：奇异值分解；滚动轴承；多故障诊断； 归一化峭度

滚动轴承是机械系统中的重要部件，常在高负荷下持续运行，容易因疲劳而磨损。在工程实际中，滚动轴承往往存在2种或多种故障耦合的情况，使得振动信号变得复杂[1]；因此，对滚动轴承复合故障进行研究具有重要的实际意义。

滚动轴承故障特征的有效提取直接影响故障诊断结果。当轴承出现局部故障时，不同故障元件的固有频率会被故障元件的通过频率调制，产生不同的周期性冲击成分，而且冲击成分幅值变化相对较快；因此，分离滚动轴承信号中的各故障成分成为提高故障诊断成功率的关键[2]。

本文以滚动轴承内外圈复合故障为研究重点，结合奇异值分解(singular value decomposition, SVD)差分谱和归一化峭度，研究滚动轴承复合故障信号特征分离方法，并通过实验验证该方法的有效性。

1理论与算法

1.1奇异值分解

奇异值分解是一种正交变换方法，在信号处理中有重要应用。假设矩阵H∈Rm×n，无论其行和列是否相关，存在正交矩阵

U=(u1,u2,…,um)∈Rm×m，

(1)

V=(v1,v2,…,vn)∈Rn×n，

(2)

使下式成立

H=USVT。

(3)

(4)

式中：diag(•)表示对角线矩阵；O表示零矩阵；q=min(m,n)，min(•)表示最小值；σi(i=1,2,…,q)称为矩阵H的奇异值，σ1≥σ2≥…≥σq>0。

记uj表示矩阵U的第j列向量，vj表示V的第j列向量，可以得到H的奇异值分解展开式

H=[u1,…,um]m×m[diag(σ1,σ2，…,σq),O]m×n

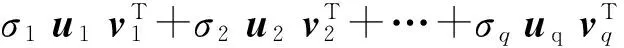
(5)

1.2矩阵空间构造

在信号处理中，应用SVD的第1步是应用采集信号构造汉克尔(Hankel)矩阵(或其他循环矩阵)。通常当采用Hankel矩阵时，SVD可以抑制信号中的噪声。

设一维时间序列

X={x(1),x(2),…,x(N)}。

(6)

其中N表示采样点数。

构造一个新的Hankel矩阵Y，具有如下形式：

Y=

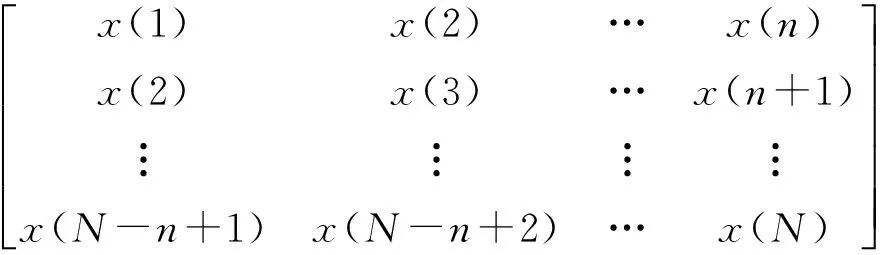
(7)

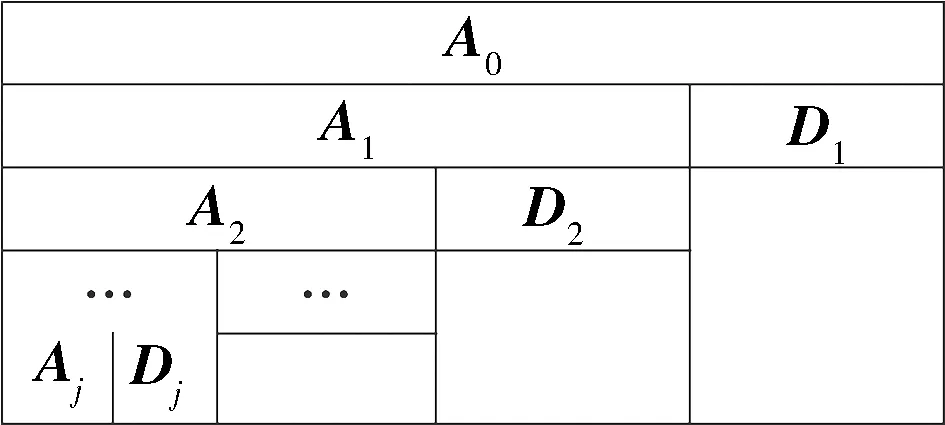
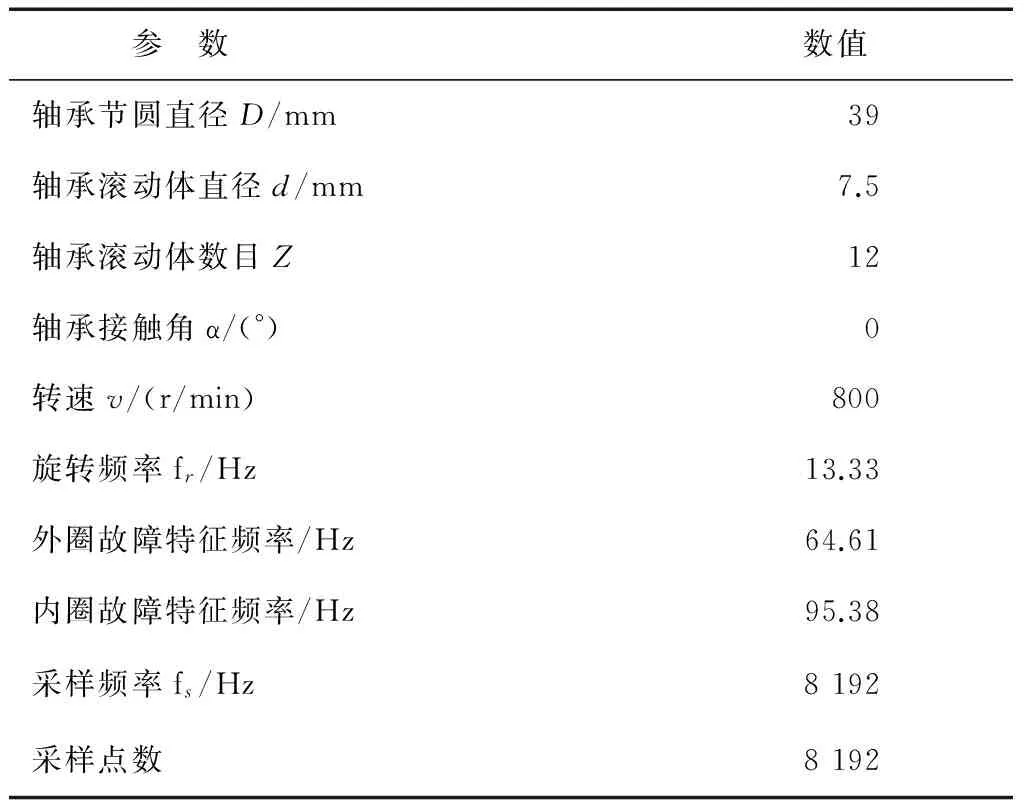
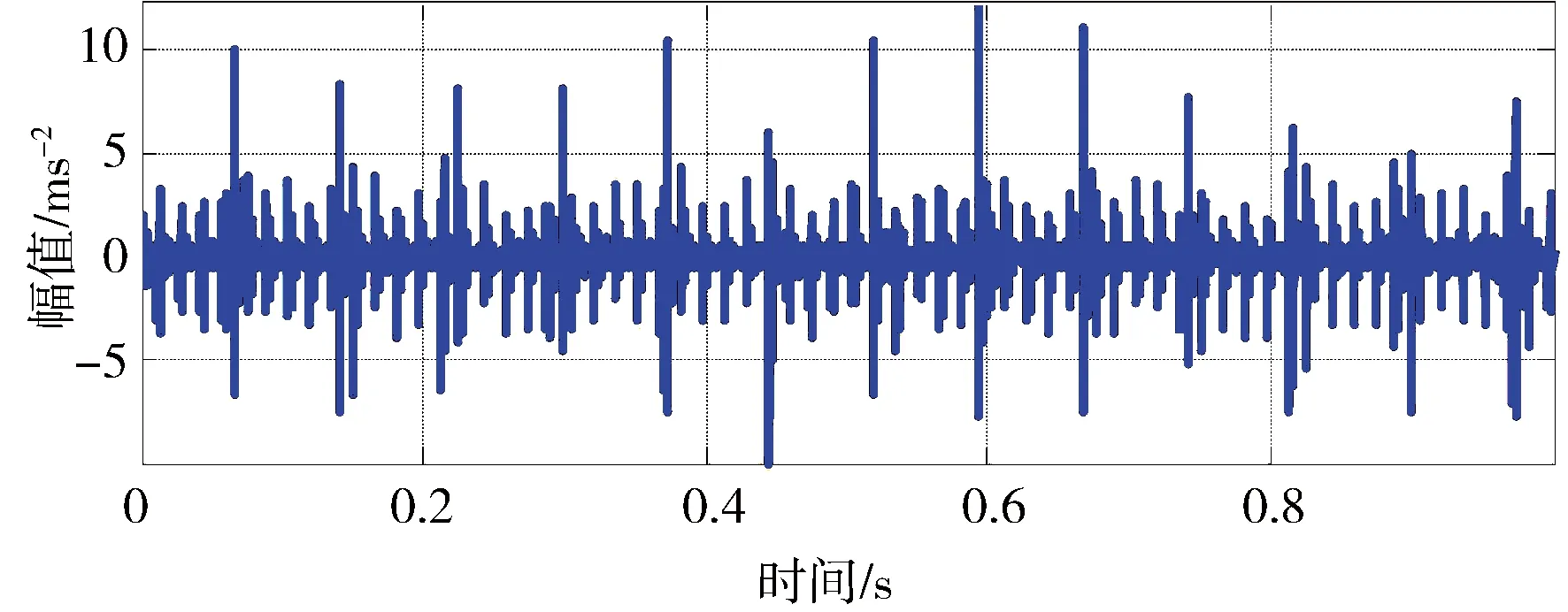
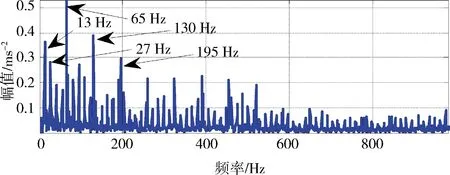
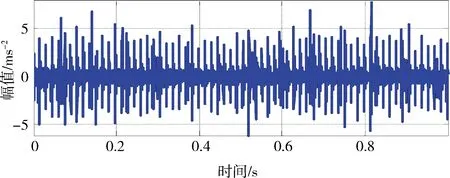
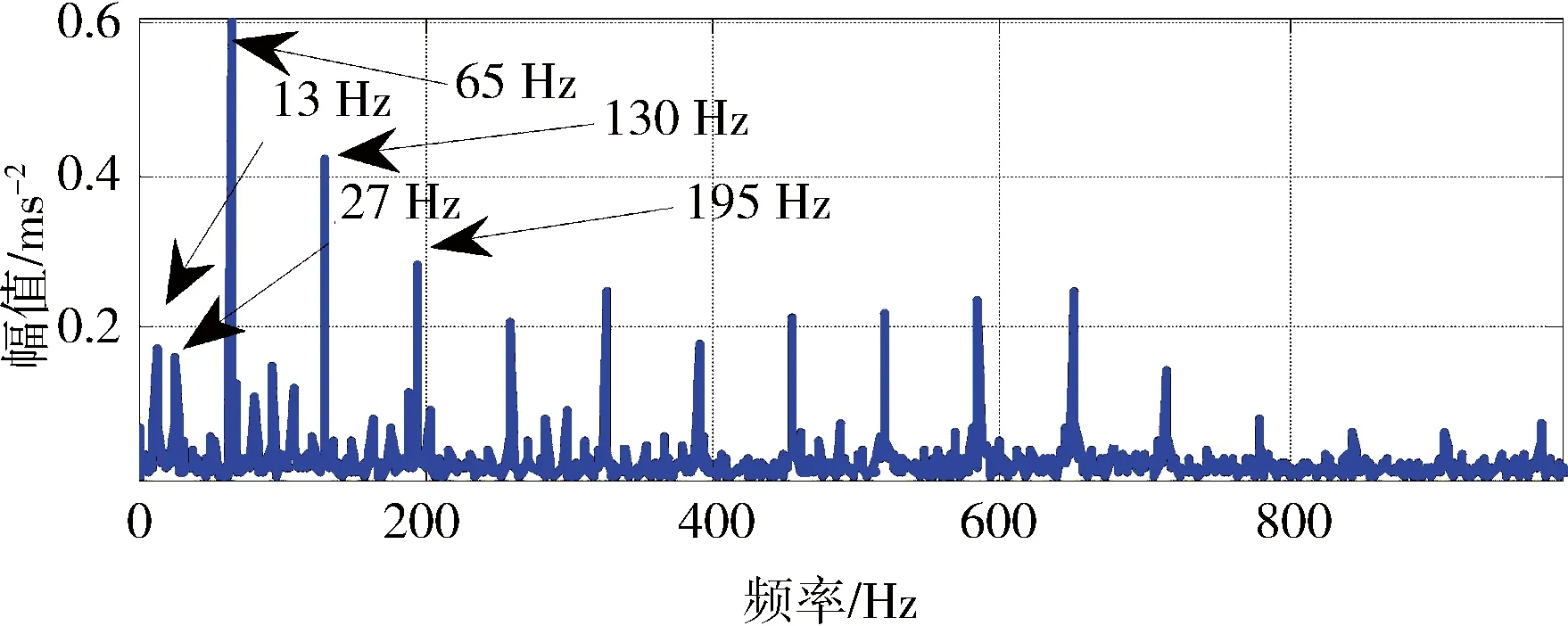
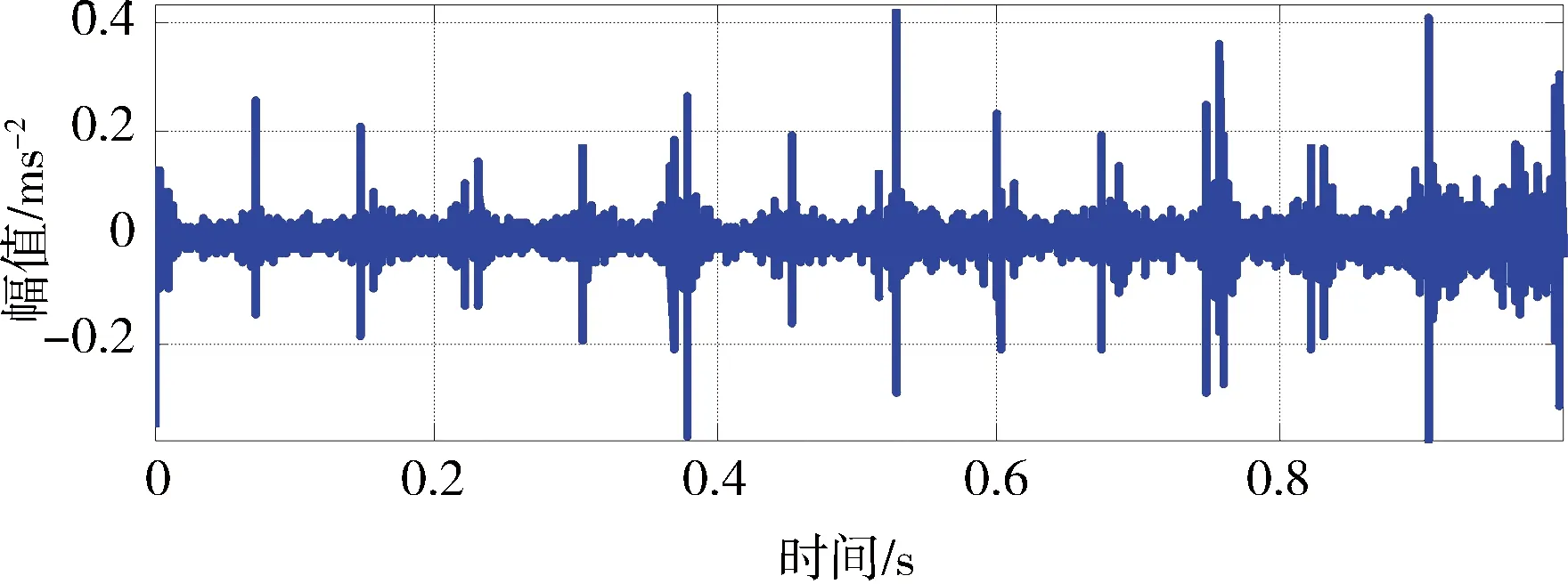
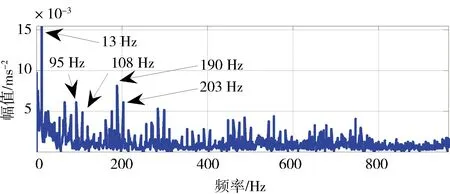
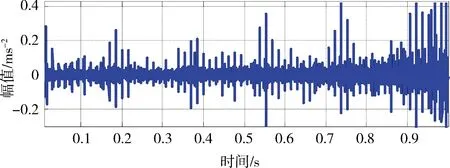
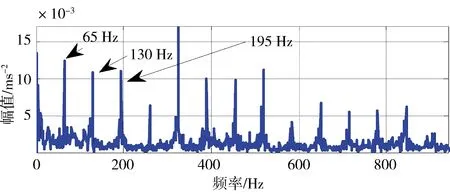
其中1

上述构造过程的本质是通过一维时间序列X的时间延迟τ=1来构造m维相空间矢量。Hankel矩阵进行奇异值分解的本质可以理解为将原始信号分解为一组分量简单的线性叠加。其意义在于通过选择感兴趣的几个分量进行简单的叠加实现信号特征信息提取[3]。为实现对信号各分量的分离，常取n=N/2，m=N/2+1。

1.3多分辨率奇异值分解

图1　信号二分递推SVD分解过程

随着对原始信号的多层分解，原信号的细节特征和主体特征逐渐显示出来。通过SVD的逆运算还可以把分解的一组近似和细节信号重构出来，如式(5)所示。这样的分解过程与小波多分辨的分解过程十分相似[4]。

1.4奇异值分解差分谱

在上述基础上，文献[5]提出一种奇异值差分谱理论。一个奇异值可以重构出一个对应的分量，通常需要舍弃一些不重要的奇异值，用剩下的奇异值来构造出较理想的降噪信号。如何确定舍弃的奇异值，可以通过差分谱有效地自动判断。

奇异值的差分谱定义为：

bk=σk+1-σkk=1,2,…,q-1；

(8)

B=(b1,b2,…,bq-1)。

(9)

式中：σk表示第k个奇异值，σk≤σk+1；B表示奇异值差分谱。

B描述了奇异值大小的变化情况。当2个奇异值差别较大时，差分谱会出现一个峰值，即梯度较大，这往往反映了轴承故障的产生。根据差分谱最大峰值点选择分量实现信号重构，从而完成故障特征信号的降噪[5]。

1.5峭度

峭度(kurtosis)是量纲一参数，定义为随机变量的四阶累积量。它描述了随机变量的概率函数同高斯分布的偏离程度。峭度对冲击信号特别敏感，适合于轴承表面损伤类故障的检测[6]。

归一化峭度(normalized kurtosis)定义为

(10)

当采集信号的分布接近正态分布时，归一化峭度等于0；当采集信号中的冲击成分增强，正态曲线出现偏斜，峭度值随之增大；当采集信号中的周期成分增强，正态曲线出现分散，峭度值随之减小。通常峭度值越大，说明轴承故障越严重。

二分递推SVD分解的结果是获得一系列信号分量DJ=[Dj(j=1,2,…，J),AJ]，从中选择合适的分量进行分析，这是诊断成功的关键。利用归一化峭度重排DJ可以获得冲击特征从强到弱的故障特征信号。

2基于奇异值分解的滚动轴承多故障诊断方法

基于上述分析，采用基于归一化峭度SVD方法进行多故障特征分离，其基本方法流程如表1所示。

表1　基于奇异值分解的滚动轴承复合故障特征分离方　　法

3实验研究

3.1实验系统

实验在旋转机械故障模拟试验台上进行。滚动轴承型号为NU205，轴承内圈随主轴旋转，外圈固定。考虑到外圈和内圈是滚动轴承大多数故障的发生部位，通过线切割分别在轴承的内圈和外圈上加工出一道宽约0.5 mm、深约1 mm的凹槽，以模拟轴承的局部故障，故障类型是内外圈复合故障。在输出轴承座的上部安装2个成90°的PCB加速度传感器，采集双通道振动信号。实验的相关参数如表2所示。

表2　实验参数

3.2实验结果

频谱分析与包络谱分析是状态监测的常用方法。在分析复合故障时，较弱的故障成分往往淹没在噪声中，影响诊断的结果。

图2和图3为传感器在水平和竖直方向采集的轴承内外圈复合故障的时间波形图及对应的包络解调谱。可以看出：采集信号有一定的冲击性；但是由于存在明显的调制现象，在频谱图中形成不同族的调制边频带。当外圈有故障时则由外圈故障频率构成调制边频带；当内圈有故障时则由内圈故障频率构成调制边频带。总之，时域振动信号成分较为杂乱，尽管能观察到多处冲击，但难以判断故障位置。

从图2、3的包络谱图中可以看出，频率成分既包含外圈故障特征频率成分又有内圈故障特征频率成分，并且外圈故障特征掩盖了内圈故障特征。2种故障特征频率在每一个包络谱图上混叠，难以确定发生的故障类型，在复合故障特征提取时容易顾此失彼，造成误诊断。

图2　水平方向传感器信号波形及其包络谱图

图3　竖直方向传感器信号波形及其包络谱图

将上述双通道采集信号应用本文算法处理，得到处理后的信号波形，如图4、5所示。可以看出，信号存在明显的周期性冲击。从图4包络谱中可以看到如下频率成分：轴旋转频率13 Hz及其倍频；特征频率95 Hz及其倍频；特征频率(95 Hz)及其倍频两侧的间隔为轴旋转频率(13 Hz)的边频等。这些频率成分分别与实际轴旋转频率13.3 Hz及其倍率、理论计算的轴承内圈特征频率95.38 Hz及倍频非常接近，因此判断滚动轴承存在内圈故障。同理，从图5可以清晰看到频率65 Hz及其倍频，与轴承外圈故障的理论特征频率64.61 Hz及其倍频非常接近，故可判断为外圈故障特征(这一频率误差是由轴承制造、转速测量和频率分辨率(Δf=1Hz)等因素导致，不影响分析结果)。总之，通过分别对比图4和图5、图2和图3可以发现滚动轴承内圈和外圈产生的调制边频带被分离出来，原来混叠的复合故障特征被成功提取为准确的单一故障特征，这有利于后续故障诊断的正确实施。

4结论

轴承内圈或外圈出现裂纹、点蚀等局部故障时，均会产生周期性冲击信号。将单故障诊断方法直接应用于多故障诊断，则可能发生误诊断。本文从复合故障诊断的角度出发，结合奇异值分解和归一化峭度优点，提出一种滚动轴承多故障诊断方法。实验结果表明，该方法可以有效地分离出滚动轴承内外圈复合故障的特征频率成分。

图4　第1个分离信号波形及其包络谱图

图5　第2个分离信号波形及其包络谱图

综上所述，可得出如下结论。

1)如果故障同时发生，通常会影响诊断的结果。当采集信号中只出现一种冲击成分，其分布曲线变得尖锐，归一化峭度值增大；当采集信号中出现多种冲击成分，分布曲线变得扁平，归一化峭度值减小。

2)多分辨奇异值分解将信号从能量的角度分解为近似和细节信号，实现信号的分离；但是如果信号成分的能量相近，该方法的处理效果不理想。

3)将对冲击信号敏感的量纲一参数峭度结合在奇异值分解重构过程中可以有效地探测出滚动轴承局部损伤类故障特征，获得冲击特征明显的单一故障特征信号，对复合故障进行分离。

本文研究为识别轴承复合故障提供了参考，具有一定的理论和工程应用价值。

参考文献

[1]Abbasion S, Rafsanjani A, Farshidianfar,et al. A Rolling Element Bearings Multi-fault Classification Based on the Wavelet Denoising and Support Vector Machine[J]. Mech Syst Signal Process,2007,21(7):2933.

[2]Purushotham V S, Narayanan P V S, Prasad S. Multi-fault Diagnosis of Rolling Bearing Elements using Wavelet Analysis and Hidden Markov Model Based Fault Recognition[J]. NDT and E International,2005,38(8):654.

[3]Zhao Xuezhi, Ye Bangyan. Similarity of Signal Processing Effect between Hankel Matrix-based SVD and Wavelet Transform and Its Mechanism Analysis[J]. Mech Syst Signal Process,2009,23(4): 1062-1075.

[4]赵学智,叶邦彦,陈统坚. 基于小波-奇异值分解差分谱的弱故障特征提取方法[J]. 机械工程学报. 2012(7): 37.

[5]赵学智,叶邦彦,陈统坚. 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报,2010,46(1): 100.

[6]张键. 机械故障诊断技术[M]. 北京：机械工业出版社2013: 62.

(编校：饶莉)

Multi-fault Feature Separation of Rolling Element Bearing Using Singular Value Decomposition and Kurtosis

WANG Yu，ZHONG Wen，YIN Yang， SONG Chunhua，TONG Jun

(SchoolofMechanicalEngineering,XihuaUniversity,Chengdu610039China)

Abstract:In order to separate multi-fault of rolling element bearing，and improve diagnosis accuracy，a method based on singular value decomposition and kurtosis was proposed. The singular value decomposition was applied to decompose the picked two-channel vibration signals. Differential spectrum of singular value decomposition and normalized kurtosis were exploited to filter and restructure the components processed by singular value decomposition respectively. Then，hilbert envelope spectrum was utilized to extract single fault feature. Finally, Examples from experimental tests show that the developed approach is effective for bearing multi-fault detection. Compared with hilbert envelope spectrum method, this method can separate weak fault components in practice and improve the ability of extracting transient impact signals. Moreover it can recognize the rolling bearing fault types and locations effectively. The approach can be used for fault detection of failures arising from local damage of rolling element bearing.

Keywords:singular value decomposition；rolling element bearing；multi-fault diagnosis; normalized kurtosis

收稿日期：2015-12-11

基金项目：国家自然科学基金资助项目(51305357)；四川省教育厅科学研究项目(13ZB0018)；西华大学重点科研基金资助项目(Z1120225)；西华大学重点实验室开放研究基金资助项目(SZJJ2012-024)。

中图分类号：TH165+.3；TP206+.3

文献标志码：A

文章编号：1673-159X(2016)03-0007-5

doi:10.3969/j.issn.1673-159X.2016.03.002

第一作者：王宇(1982—),男,讲师,博士,主要研究方向为机械设备状态监测与故障诊断。E-Mail：redtu160@163.com

·机电工程·