考虑运动副间隙的函数机构稳健设计

李欣玲，张均富，佘　霞， 李玉娟

(西华大学机械工程学院，四川 成都　610039)



·机电工程·

考虑运动副间隙的函数机构稳健设计

李欣玲，张均富*，佘霞， 李玉娟

(西华大学机械工程学院，四川 成都610039)

摘要：机构的随机因素使其运动输出在名义值附近波动，从而导致机构的运动精度和可靠性降低。为降低机构运动输出对随机因素的敏感度，提高机构运动品质，提出一种考虑构件尺寸公差和运动副间隙等随机因素的机构稳健设计方法。首先应用截尾混合降维法建立间隙机构运动误差的概率模型，然后采用田口质量损失函数导出机构运动的质量损失函数，再以此建立机构的稳健设计模型，最后以平面四杆函数机构综合为例，验证其方法的有效性。结果表明，该方法能够有效提高机构运动的稳健性，其设计所得机构的运动误差的平均均值和平均标准差分别比原机构减小55%和25%。

关键词：运动副间隙；运动综合；稳健设计；函数机构

机构的不确定性主要来源于材料属性的分散性、尺寸公差、运动副间隙、装配误差以及运动过程中铰链磨损的随机性等。相比而言，运动副间隙对机构运动输出不确定性影响最大。运动副间隙的随机性可以传播到机构系统的运动输出，严重地影响机构运动的输出精度、动力学性能以及可靠性。随着现代机械系统向高精度、高可靠和长寿命发展，考虑环境和自身具有的不确定性的真实机构系统设计必然成为重要研究课题。真实机构的设计必然涉及机构运动副的间隙问题[1]。

含运动副间隙的机构运动学研究，主要是评价运动副间隙对机构运动精度的影响。其处理方法有2种：确定性方法和不确定性方法。确定性方法的基本思路是将间隙处理成虚拟杆，进而开展平面连杆机构的运动精度分析和运动综合[2-3]。在空间机构方面有学者采用虚功原理[4]、旋量方法[5-6]等，对机构的位置误差进行研究。在不确定方法方面，学者将区间代数[7]或概率统计理论[8-16]用于机构的运动分析与综合。概率统计方法主要用概率密度函数描述运动副间隙的随机行为。概率方法虽不能揭示运动副的接触状态，但是对研究机构运动可靠性方面是一种重要的方法。现有文献中，一般均匀分布或正态分布常被用于建立运动副间隙的概率模型[8,14]；但是，对含运动副间隙的机构可靠性问题分析，采用一次二阶矩(FOSM)方法和一阶可靠性(FORM)方法均会存在较大误差，因为运动副销轴中心被约束在间隙圆内而使运动副间隙变量之间统计相关。为处理间隙变量的相关性，有学者提出了混合降维方法(hybrid dimension reduction method，HDRM)，该方法能够很好地平衡可靠度求解的效率和精度问题，现已被用于平面函数机构的可靠性分析和概率综合[8,14-16]。本文在上述研究的基础上，进一步研究含运动副间隙的机构稳健综合方法，以期降低机构运动精度性能指标对系统存在的不确定性的敏感，提升机构系统的运动品质。

1机构的运动误差概率模型

图1所示为含运动副间隙的平面四杆机构。假定构件尺寸Li(i=1,…,4)为服从正态分布的独立随机变量，并记L=(L1,…,L4)，则L～N(μL,σL)，其中μL=(μL1,…,μLn)，σL=(σL1,…,σLn)。Ci(i=1,…,4)为机构回转副，其间隙大小为rC(rC=rB-rJ,其中rB表示轴承半径，rJ表示轴颈半径)。

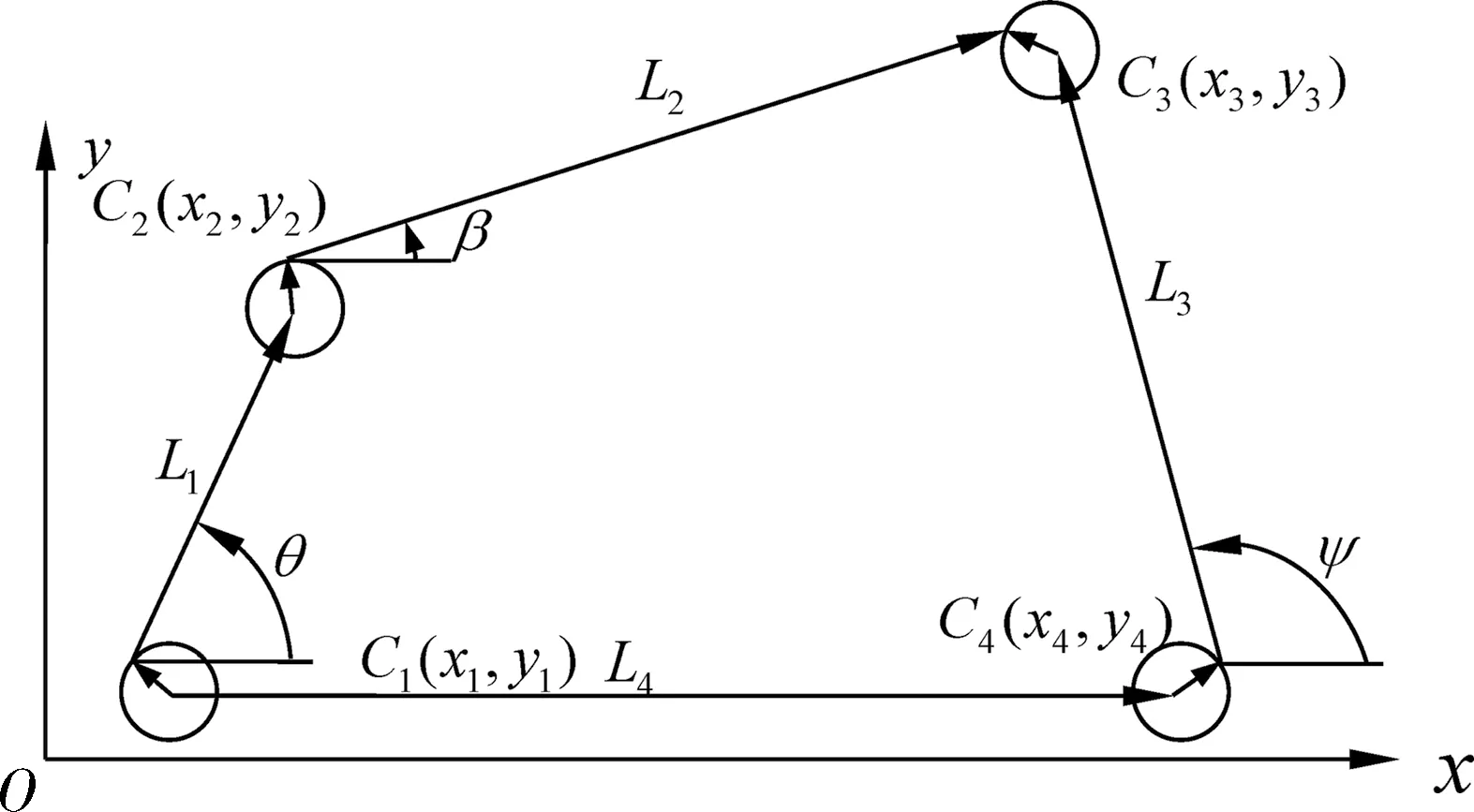
图1　含运动副间隙的四杆机构

以轴承孔几何中心为参考点建立该运动副的局部坐标系，则轴颈几何中心在其对应局部坐标系中的位置为Cj(Xj,Yj)，(j=1,…,4)，如图2所示。轴颈中心坐标Xj、Yj为统计相关的随机变量，这里假设其在间隙圆内服从均匀分布，则有

(1)

假设机构的真实运动输出为ψ(S,θ)，期望输出为ψd(θ)，则机构的运动误差可定义为

g(S,θ)=ψ(S,θ)-ψd(θ)。

(2)

式中：S=(L,(X,Y))；L=(L1,…,L4)为机构尺寸变量；(X,Y)=((X1,Y1),…,(X4,Y4))为机构的运动副变量；g(S,θ)为机构运动误差函数。

将式(2)改写为

g(S,θ)=[ψ(S,θ)-ψ(μS,θ)]+[ψ(μS,θ)-ψd(θ)]。

(3)

由式(3)可见，机构的运动误差包括结构误差gstruct=ψ(μS,θ)-ψd(θ)和随机误差grand=ψ(S,θ)-ψ(μS,θ)。

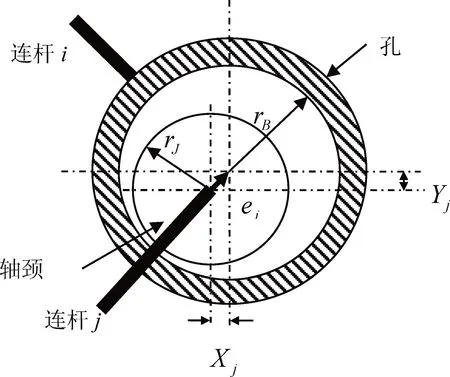
图2　运动副间隙

对误差函数g(S,θ)截尾降维处理[8,14]得到

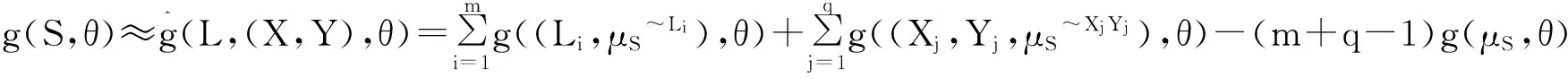
(4)

进一步简化得到

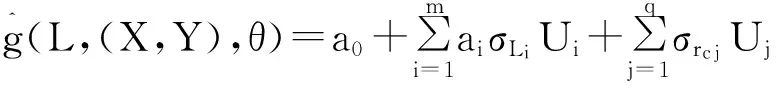
(5)

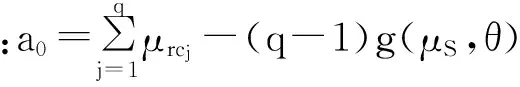
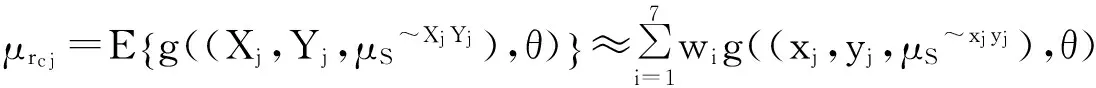
(6)

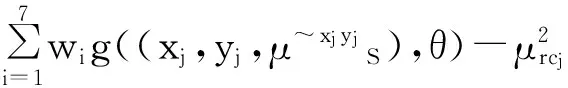
(7)

根据式(5), 误差函数g(S,θ)的均值为

μg(S,θ)≈a0。

(8)

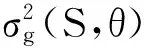
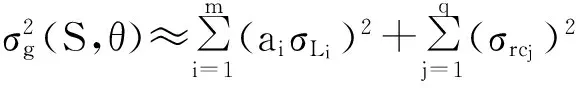
(9)

2机构的稳健性评估

开展稳健设计，定义产品质量损失函数是重要环节。通常，稳健设计中质量指标定义为对产品质量或用户满意度有着重大影响的重要响应。对于机构的稳健设计，机构的运动误差即为其质量指标。由于在考虑机构综合时以追求运动误差等于0为目标，因此该质量特性属于名义值最好类型(the nominal-the-best type)[17]。由此可见，当运动误差等于目标值时，机构具有最佳品质。

对于非精确点机构综合，其结构误差一般不等于0，因此其质量指标偏离目标值。此外，由于随机误差的存在，机构的实际运动误差在其结构误差附近波动。根据田口稳健性设计理念，机构的运动误差所具有的偏差会引起系统的质量损失。稳健设计中，常用田口质量损失函数[18]度量系统的质量损失。现假设机构的质量函数为Q，Q为机构运动误差g(X,θ)及其目标值的二次函数。若将质量函数Q在目标值t处进行泰勒二阶展开，由于质量函数Q(t)=0且为最小，则Q′(t)=∂Q/∂t=0；因此，质量损失函数可以表示为

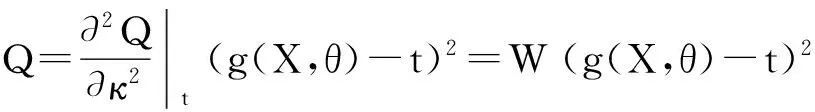
(10)

式中：t=0为运动误差g(X,θ)的目标值；W=∂2Q/∂t2由质量损失模型确定。

由于质量函数Q为机构运动误差g(X,θ)的函数，因此Q为随机变量函数，其期望常被用于稳健设计。质量函数Q的期望

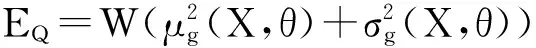
(11)

考虑到机构运动误差g(X,θ)为机构曲柄转角θ的函数，因此，对应于指定曲柄转角θ处有

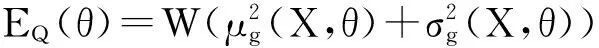
(12)

在分析时需要对机构指定运动区间离散，因此采用各离散点处质量函数期望的平均值作为机构运动的质量损失，即

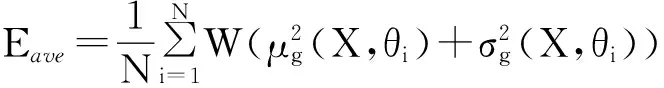
(13)

将式(8)、(9)代入式(13)即可进行机构的稳健性评估。

3机构的稳健设计模型

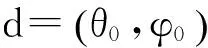
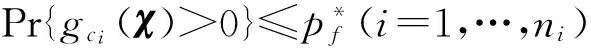
(14)

μL≤μ≤μU；

dL≤d≤dU。

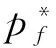
4实例分析

用图1所示曲柄摇杆机构实现正弦函数y=arctanx(x∈[0,1])，机构运动的输入输出范围分别为Δθ=100°和Δψ=45°。机构运动输出的允许误差限为ε=0.4。设机构的尺寸变量Li(i=1,…,4)服从正态分布，其标准差σLi=0.05，运动副间隙Cj(Xj,Yj)服从均匀分布，间隙半径rc=0.02mm。

根据图1，将机构的曲柄存在条件、传力性能约束处理为可靠性约束并采用一次二阶矩(FOSM)方法求解可靠度，即

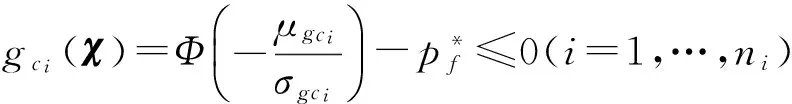
(15)

式中：μgci、σgci分别为gci(χ)的均值和方差，其中

gc1(χ)=L1-min(L2,L3,L4)≤0 ，

(16)

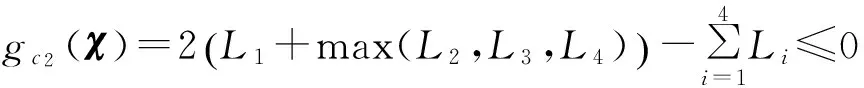
(17)

gc3(χ)=γL-min(γ1,γ2)≤0 ，

(18)

gc4(χ)=max(γ1,γ2)-γU≤0；

(19)

γL和γU分别为传动角γ的许用下限和上限；γ1,γ2为机构主动件与曲柄共线的两位置处的传动角，即

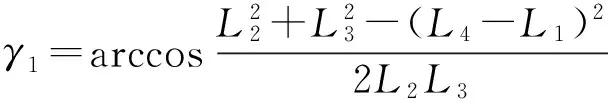
(20)

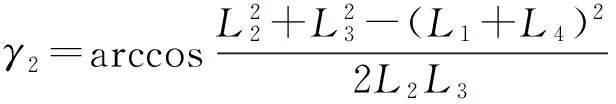
(21)

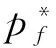
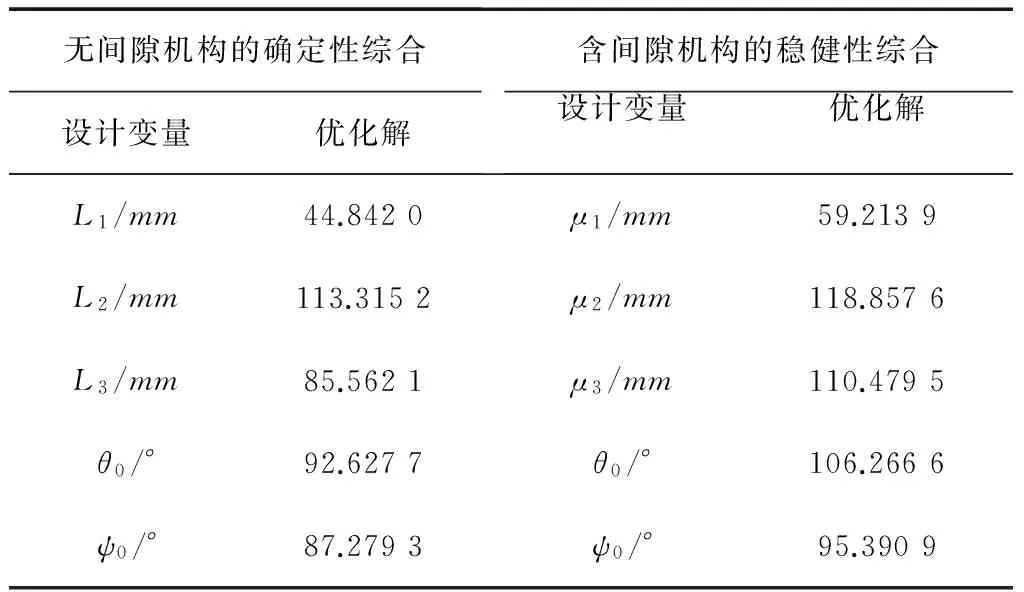
表1　机构综合的优化解

考虑机构的运动副间隙，采用截尾降维方法对确定性综合解和含间隙的稳健性解进行机构输出误差概率分析。图3、图4分别为2种综合方法所得机构运动误差均值和方差。可以看出，采用稳健设计并考虑机构运动副间隙所得机构的运动误差的均值、标准差或方差均有明显减小。相比原机构，新设计方法所得机构的运动误差的平均均值和平均标准差分别比原机构减小55%和25%。

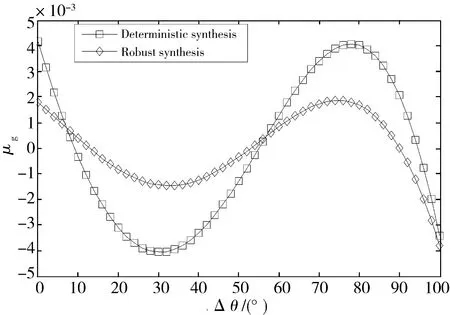
图3　机构输出误差均值

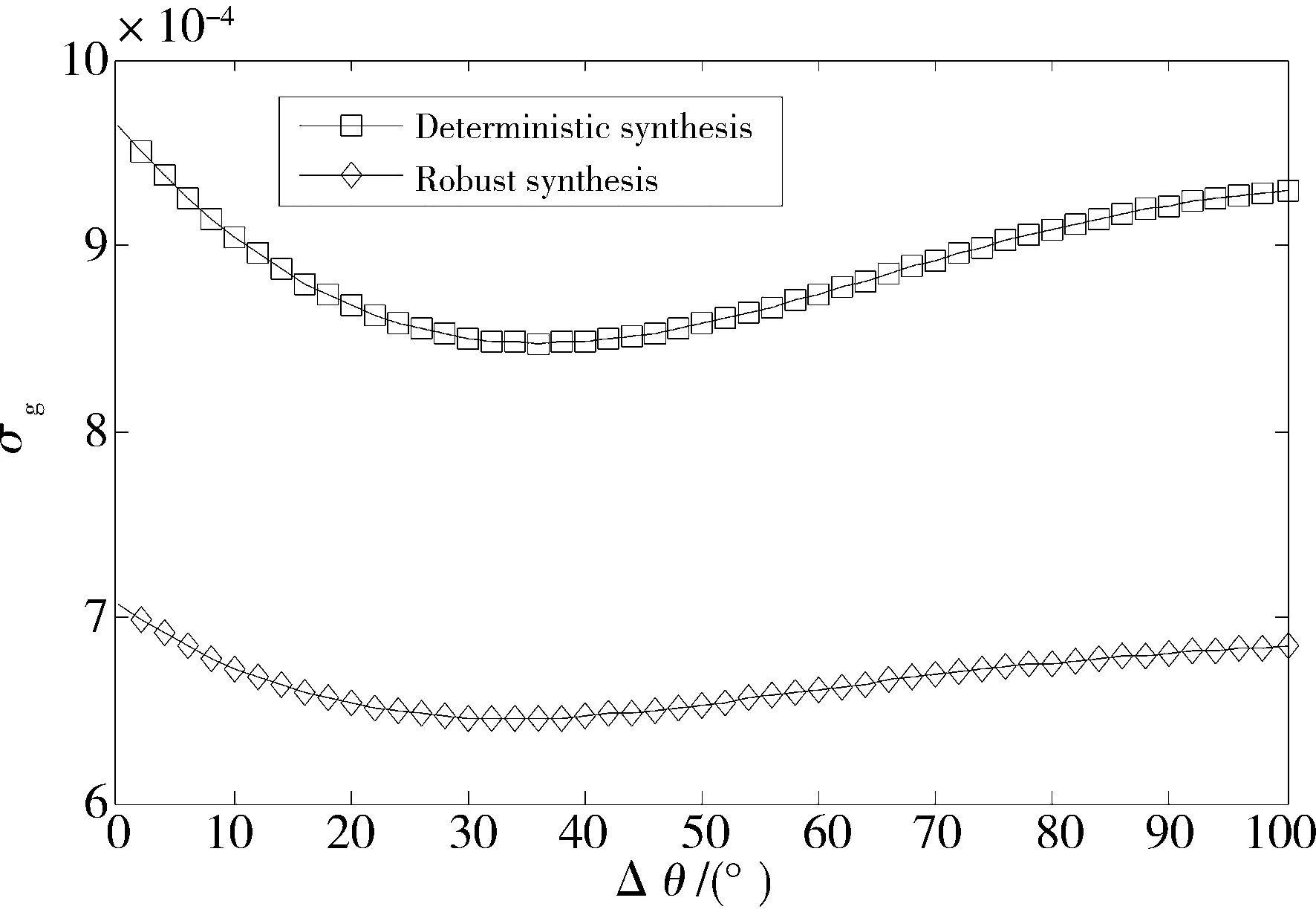
图4　机构输出误差标准差

5结论

在刚性机构系统的不确定性因素中，运动副间隙对机构运动精度影响最大。为降低运动精度对运动间隙的敏感，提出一种同时考虑构件尺寸公差和运动副间隙等随机因素的稳健综合方法。建模时采用田口质量损失函数导出机构运动精度质量损失模型，并采用截尾降维算法导出间隙机构运动误差的均值和方差。基于此，建立以质量损失最小为目标的平面四杆函数机构的稳健设计模型。数值实例表明，所提出的方法能够有效减小机构运动误差的均值和方差、降低运动精度对随机因素的敏感。该方法为高精度、高可靠、稳健性好的机构系统设计提供了参考。

参考文献

[1]PARENTI-CASTELLI V,VENANZI S.Clearance Influence Analysis on Mechanisms[J]. Mechanism and Machine Theory,2005,40(12): 1316.

[2]Feng B, Morita N, Torii T. A New Optimization Method for Dynamic Design of Planar Linkage with Clearances at Joints[J]. Journal of Mechanical Design, 2002,124(1): 68.

[4]Innocenti C. Kinematic Clearance Sensitivity Analysis of Spatial Structures with Revolute Joints[J]. Journal of Mechanical Design, 2002, 124(1): 52.

[5]FRISOLI A,SOLAZZI M,PELLEGRINETTI D,et al. A New Screw Theory Method for the Estimation of Position Accuracy in Spatial Parallel Manipulators with Revolute Joint Clearances[J]. Mechanism and Machine Theory, 2011, 46(12): 1929.

[6]MENG jian,ZHANG Dongjun,LI Zexiang.Accuracy Analysis of Parallel Manipulators with Joint Clearance[J].Journal of Mechanical Design, Transactions of the ASME,2009,131(1): 011.

[7]WU Weidong,RAO S S.Uncertainty Analysis and Allocation of Joint Tolerances in Robot Manipulators Based on Interval Analysis[J].Reliability Engineering and System Safety,2007,92(1): 54.

[8]Wang Jinge,Zhang Junfu,Du Xiaoping.Hybrid Dimension Reduction for Mechanism Reliability Analysis with Random Joint Clearances[J].Mechanism and Machine Theory,2011,46(10): 1396.

[9]DHANDE S G,CHAKRABORTY J.Mechanical Error Analysis of Spatial Linkages[J].Journal of Mechanical Design,1978,100(4):732.

[10]Xu W, Zhang Q. Probabilistic Analysis and Monte Carlo Simulation of the Kinematic Error in a Spatial Linkage[J]. Mechanism and Machine Theory, 1989, 24: 19.

[11]孟宪举,张策,詹梅晶,等.含间隙连杆机构精度概率分析模型[J].机械设计，2004，21(9)：35.

[12]黄玮,冯蕴雯,吕震宙,等. 考虑铰链运动副间隙的机构运动可靠性分析模型[J].机械强度, 2007, 29(2): 264.

[13]邹文韬,王志刚,张均富. 含运动副间隙的平面函数机构运动点可靠性分析[J].工程设计学报, 2013, 20(5): 409.

[14]Zhang Junfu, Du Xiaoping. Time-Dependent Reliability Analysis for Function Generation Mechanisms with Random Joint Clearances[J]. Mechanism and Machine Theory, 2015, 92:184.

[15]张均富,汪勇,徐红,等. 齿轮齿条转向机构的时变可靠性分析[J]. 西华大学学报(自然科学版),2012,31(6):20.

[16]李玉娟,张均富.考虑运动副间隙的平面函数机构概率综合[J]. 机械设计与研究,2015,31(1): 14.

[17]Wu F C, Chyu C C. Optimization of Robust Design for Multiple Quality Characteristics[J]. International Journal of Production Research, 2004, 42 (2): 337.

[18]Taguchi G, Chowdhury S, Taguchi S. Robust Engineering[M]. New York:McGraw Hill, 2000.

(编校：饶莉)

Robust Synthesis of Planar Function Mechanisms with Joint Clearance

LI Xinling，ZHANG Junfu*， SHE Xia，LI Yujuan

(SchoolofMechanicalEngineering,XihuaUniversity,Chengdu610039China)

Abstract:The random factors in the mechanisms make the output of the motion fluctuate around the nominal value. The fluctuation leads to the reduction of movement precision and reliability of the mechanism. In order to reduce the sensitivity of mechanism motion output which effected by uncertainty and improve the quality of mechanism motion, we propose a robust synthesis approach which taking random factors such as links dimensional tolerances and joint clearances etc into account. First the hybrid dimensional reduction method (HDRM) was used to establish the probability model of mechanism motion error with clearances. Then the Taguchi quality loss function was introduced to derivate the quality loss function of motion of mechanism, and the robust design model of planar path mechanism was established. Finally, the synthesis of planar function mechanism was given to illustrate the effectiveness of the proposed method. Verification result shows that the new design method can improve the robustness of mechanical motion effectively which was proposed in the paper, the average mean and mean standard deviation of motion error of designed mechanism reduced by 55% and 25%, respectively, which were lower than original mechanisms’.

Keywords:joint clearance; kinematic synthesis; robust design; function mechanisms

收稿日期：2016-01-08

基金项目：国家自然科学基金资助项目(51275425)；四川省教育厅项目(12zz008)。

*通信作者：张均富 (1972—)，男，教授，博士，主要研究方向为机器人与机电一体化、 概率工程设计。E-mail：zhang_junfu@126.com

中图分类号：TH112；TH115

文献标志码：A

文章编号：1673-159X(2016)03-0012-4

doi:10.3969/j.issn.1673-159X.2016.03.003