基于广义粒子加耦合振子链模型的非各态历经研究

卢　宏，吕　艳

(1.西华大学理学院，四川 成都　610039；2.太原科技大学应用科学学院，山西 太原　030024)



基于广义粒子加耦合振子链模型的非各态历经研究

卢宏1，吕艳2

(1.西华大学理学院，四川 成都610039；2.太原科技大学应用科学学院，山西 太原030024)

摘要：构建广义粒子加耦合振子链模型，模型包含气体分子与固体振子链的4类耦合方式。在广义朗之万方程框架下，分析气体分子的非各态历经性。研究表明：不同耦合方式将引起不同性质的记忆阻尼核函数和功率谱函数，这是气体分子变量呈现不同长时渐进行为的内在原因；坐标与坐标耦合导致气体分子的坐标是一个非各态历经变量，速度相关耦合导致速度是一个非各态历经变量。

关键词：耦合振子链；广义朗之万；噪声谱；非各态历经

气体分子与固体表面非弹性碰撞一直引发人们在理论和实验上的浓厚兴趣[1-3]。 研究这一问题使用最广的是Zwanzig模型[4]，即将固体表面简化为一维半无界耦合简谐振子链。Zwanzig模型被广泛应用于解释大量物理、化学和生物现象，例如气固散射[5-7]、晶格振动[8-9]、热传导[10-11]、凝相化学反应[12-13]和蛋白质吸附[14]。文献[15-16]研究表明Zwanzig模型可以通过对角化技术转变为独立简谐振子的Caldeira-Leggett (CL)模型。文献[17]提出包含4种耦合方式的广义CL模型，指出速度相关耦合引起自由粒子的弹道扩散和非各态历经行为，即粒子的稳态速度二次矩依赖其初始准备。当对Zwanzig模型考虑4种耦合方式时，即气体分子坐标与自由端振子坐标耦合、气体分子坐标与自由端振子速度耦合、气体分子速度与自由端振子坐标耦合、气体分子速度与自由端振子速度耦合，气体分子是否会出现非各态历经现象？

本文探讨与一端固定的有限数目简谐振子链耦合的气体分子的非各态历经行为。构建广义粒子加耦合振子链模型，分析4种耦合方式所对应的记忆阻尼核函数的性质及其各态历经性。

1广义粒子加耦合振子链模型

考虑构建广义粒子加耦合振子链模型(如图1所示)，它包括气体分子与自由端振子间的4类耦合：1) 气体分子坐标与自由端振子坐标(c-c)耦合；2)气体分子坐标与自由端振子速度(c-v)耦合；3)气体分子速度与自由端振子坐标(v-c)耦合；4)气体分子速度与自由端振子速度(v-v)耦合。它们的耦合系数分别记为Ccc、Ccv、Cvc、Cvv。假定气体分子和简谐振子的质量M=m=1，则整个系

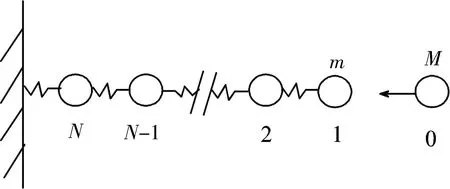
图1　气体分子与一端固定的简谐振子链耦合模型示意图

统的哈密顿量写为如下形式：

(1)

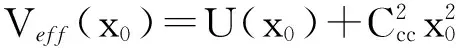
利用正则变换，哈密顿量式(1)改写为如下形式：

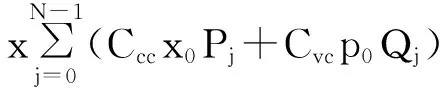
(2)

其中Γj与ωj的定义式分别写作

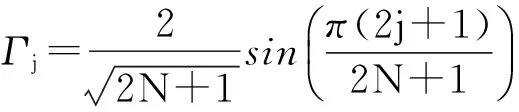
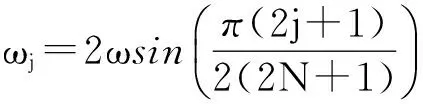
(3)

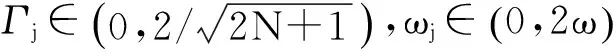
2广义朗之万方程

从哈密顿量式(2)出发，消除热浴振子坐标自由度，得到气体分子所满足的广义朗之万方程

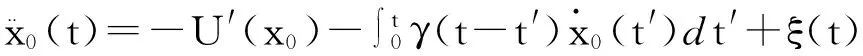
(4)

其中，记忆阻尼核函数γ(t)和随机力ξ(t)分别定义如下：

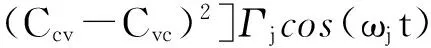
(5)

〈ξ(t)〉=0,〈ξ(t)ξ(s)〉=kBTγ(t-s)。

(6)

把Γj和ωj的定义式(3)代入式(5)，得到记忆阻尼核函数γ(t)的完全表达式

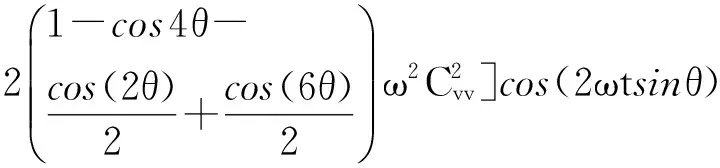
(7)

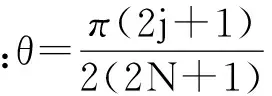
J4(2ωt)-J2(2ωt)/2+J6(2ωt)/2]。

(8)

其中Jν(t)是Bessel函数。

3功率谱分析

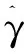
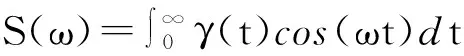
(9)

分别考虑3种情况：Ccc≠0,Ccv≠0(或Cvc≠0,),Cvv≠0，其余3类耦合系数取为零。 图2给出3类噪声的功率谱。可见，c-v(或者v-c) 和v-v耦合相对应的S(ω)在零频处消失，而c-c对应的S(ω)在零频处是一个常数。不同的谱类型将导致其驱动的粒子呈现不同的长时动力学行为。速度相关耦合引起的噪声与简谐速度噪声类似，都呈现带通行为[19]。与广义CL模型不同，v-v耦合引起的噪声是HVN类型，而非简谐加速度噪声[20-21]，这是由于正则模频率具有阈值所导致的结果。

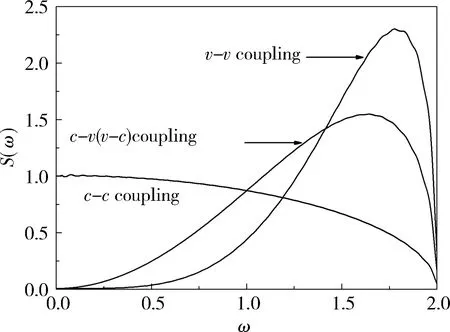
图2　功率谱随频率变化示意图

对方程(9)利用Bessel函数Jν(t)的拉普拉斯变换

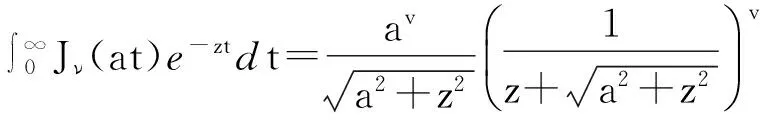
(10)

推导得到记忆阻尼核函数γ(t)的拉普拉斯变换形式

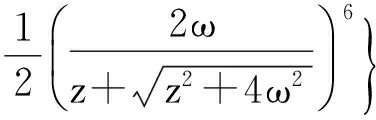
(11)

分析极限情形，取z→0，有：

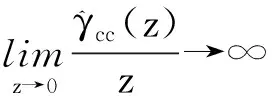
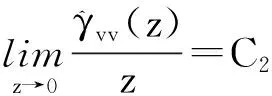
(12)

可见对于本文所提出的广义粒子加耦合振子链模型，广义布朗运动的各态历经条件

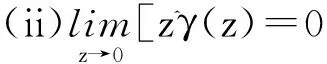
(13)

只有在c-c耦合方式下才成立；对于速度相关耦合不满足(13)式的第一个必要条件，在长时极限下气体分子的速度二次矩依赖其初始速度条件，这是第一类非各态历经运动。

4结论

本文构建了广义粒子加耦合振子链模型，考虑气体分子与自由端振子的4类耦合方式：1)气体分子坐标与自由端振子坐标耦合；2)气体分子坐标与自由端振子速度耦合；3)气体分子速度与自由端振子坐标耦合；4)气体分子速度与自由端振子速度耦合。通过与粒子加独立振子模型的比较，发现2者并不等价。研究发现不同的耦合方式引起不同的阻尼或者噪声谱，坐标与坐标双线性耦合导致气体分子的坐标是一个非各态历经变量，而速度相关耦合导致气体分子的速度是一个非各态历经变量。不同的耦合形式会导致怎样的长时间动力学行为将是值得进一步探寻的方向。

参考文献

[1]Ford G W, Kac M, Mazur P. Statistical Mechanics of Assemblies of Coupled Oscillators [J]. Mathematical Physics in One Dimension, 1966:524.

[2]Ford G W, Lewis J T, O'Connell R F. Dissipative Quantum Tunneling: Quantum Langevin Equation Approach [J]. Physics Letter A, 1988, 128(1/2): 29.

[3]Rosa J, Beims M W. Dissipation and Transport Dynamics in a Ratchet Coupled to a Discrete Bath [J]. Phys Rev E, 2008, 78: 031126.

[4]Zwanzig R W. Collision of a Gas Atom with a Cold Surface [J]. J Chem Phys, 1960, 31: 1173.

[5]Plyukhin A V, Schofield J. Trapping, Reflection, and Fragmentation in a Classical Model of Atom-Lattice Collisions [J]. Phys Rev E, 2002, 65: 026603.

[6]Lu Hong, Bao Jingdong. Time Evolution of a Harmonic Chain with Fixed Boundary Conditions [J]. Chin Phys Lett, 2011, 28: 040505.

[7]Lu Hong, Bao Jingdong. Nonergodic Brownian Motion in a Collinear Particle-Coupled Harmonic Chain Model [J]. Chin Phys Lett, 2013, 30: 010502.

[8]Kim J, Sawada I. Dynamics of a Harmonic Oscillator on the Bethe Lattice [J]. Phys Rev E, 2000, 61: R2172.

[9]Barrio R A, Galeener F L, Martinez E. Vibrational Bethe Lattice with Random Dihedral Angles [J]. Phys Rev Lett, 52: 1786.

[10]Gendelman O V, Savin A V. Normal Heat Conductivity of the One-Dimensional Lattice with Periodic Potential of Nearest-Neighbor Interaction [J]. Phys Rev Lett, 2000, 84: 2381.

[11]Segal D. Absence of Thermal Rectification in Asymmetric Harmonic Chains with Self-Consistent Reservoirs [J]. Phys Rev E, 2009, 79: 012103.

[12]Adelman S A, Doll J D. Generalized Langevin Equation Approach for Atom/Solid-Surface Scattering: Collinear Atom/Harmonic Chain Model [J]. J Chem Phys, 1974, 61: 4242.

[13]Doll J D, Myers L E. Generalized Langevin Equation Approach for Atom/Solid-Surface Scattering: Inelastic Studies [J]. J Chem Phys, 1975, 63: 4908.

[14]李艺，程时. 蛋白质在固体表面吸附的研究进展 [J]. 高分子通报, 2007(3): 41.

[15]Caldeira A O, Leggett A J. Influence of Dissipation on Quantum Tunneling in Macroscopic Systems [J]. Phys Rev Lett, 1981, 46: 211.

[16]Lievens S, Stoilova N I, Van der Jeugt J. Harmonic Oscillator Chains as Wigner Quantum Systems: Periodic and Fixed Wall Boundary Conditions in gl(1|n) Solutions [J]. Journal of Mathematical Physics ,2008, 49: 073502.

[17]Bai Zhanwu, Bao Jingdong, Song Yanli. Classical and Quantum Diffusion in the Presence of Velocity-Dependent Coupling [J]. Phys Rev E, 2005, 72: 061105.

[18]Razavy M. Classical and Dissipative Quantum Systems [M]. London :Imperial College Press, 2005.

[19]Bao Jingdong, Zhuo Yizhong. Ballistic Diffusion Induced by a Thermal Broadband Noise [J]. Phys Rev Lett, 2003, 91: 138104.

[20]Bao Jingdong, Zhuo Yizhong. Anomalous Dissipation: Strong non-Markovian Effect and its Dynamical Origin [J]. Phys Rev E, 2005, 71: 010102(R).

[21]卢宏, 覃莉, 包景东. 周期场中非各态历经布朗运动 [J]. 物理学报, 2009, 58(12): 8127.

(编校：叶超)

Studies of the Nonergodicity Based on a Generalized Particle-plus-coupled-oscillator Chain Model

LU Hong1,LV Yan2

(1.SchoolofScience,XihuaUniversity,Chengdu610039China;2.SchoolofAppliedScience,TaiyuanUniversityofScienceandTechnology,Taiyuan030024China)

Abstract:An generalized particle-plus-coupled-oscillator chain model was established. It includes four kinds of couplings between the gas particle and the coupled chain. With the generalized Langevin equation, the nonergodicity of the gas particle was investigated. The results show that different coupling ways leads to different damping kernels and spectrum functions, which reveal the underlying cause of the different long time asymptotic behaviors of the gas particle. Coordinate-coordinate coupling can induce the coordinate of the gas particle to be a nonergodic variance; while velocity relative coupling leads to the velocity nonergodicity.

Keywords:coupled chain; generalized Langevin; noise spectrum; nonergodicity

收稿日期：2015-03-23

基金项目：四川省教育厅青年基金(13233683)；西华大学重点科研基金(z1123330)。

中图分类号：O414.2

文献标志码：A

文章编号：1673-159X(2016)03-0063-3

doi:10.3969/j.issn.1673-159X.2016.03.013

第一作者：卢宏(1985—)，女，讲师，博士，主要研究方向为统计物理。

·基础学科·