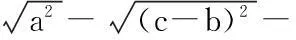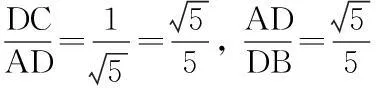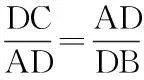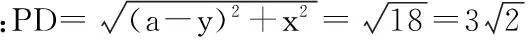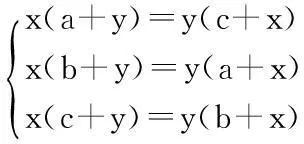“数形结合”在中学数学中的妙用

陈　博

安源一中，江西　萍乡　337000



“数形结合”在中学数学中的妙用

陈博

安源一中，江西萍乡337000

摘要：作为一种重要的数学思想，同时也是一种常用的解题模式，巧妙利用“数形结合”的可以使一些抽象的数学问题变得直观和形象，这种审视问题呈现方式的改变可以变抽象思维为形象思维，有助于把握数学问题的本质，并得到更为简捷的解题方法和技巧。

关键词：数形结合；形数结合；数学思想；解决问题

数形结合思想是指将数(量)与(图)形结合起来进行分析、研究、解决问题的一种思想策略。

著名数学家华罗庚先生说：“数与形，本是相倚依，怎能分作两边飞，数缺形时少直觉，形少数时难入徽，数形结合百般好，隔离分家万事休”。这充分说明了数形结合思想在数学研究和数学应用中的重要性。“数”和“形”在哲学中是矛盾的一对，既对立又统一，单独地论数，解题思路就缺少直观性，单纯地论形，又在解题中缺少严密性。只有把二者相结合，才能使抽象复杂的数量关系，通过几何图形直观地表现，并通过数量间的计算、分析，达到更加完整、严密、准确。因此我们在研究解决数学问题时要善于由形思数，由数思形，数形结合。

一、利用数形结合思想加深对基础知识的理解

利用数轴理解相反数的概念，便具有了几何意义，互为相反数的两个数在数轴上实质上是它们到原点的距离相等，方向相反。一个数的绝对值就是数轴上表示这个数的点与原点的距离。一元一次不等式组的解集是借助数轴找各个不等式解集的公共部分。平面直角坐标系建立后使有序实数对具有了几何意义，由点可确定点的坐标，由坐标可确定点，一次函数、二次函数、反比例函数只有利用它们的图象，才能更深刻地理解它们的性质。解直角三角形的应用更是数形结合的典型材料。总之，数与形的结合使得代数与几何紧密相联，息息相关，使得数学更具有生机和活力。

二、由数思形，数形结合，用形解决数的问题

案例1：已知 ， a>0,b<0,a+b<0，用“<”号把a,-a,b,-b连接起来。

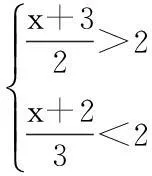
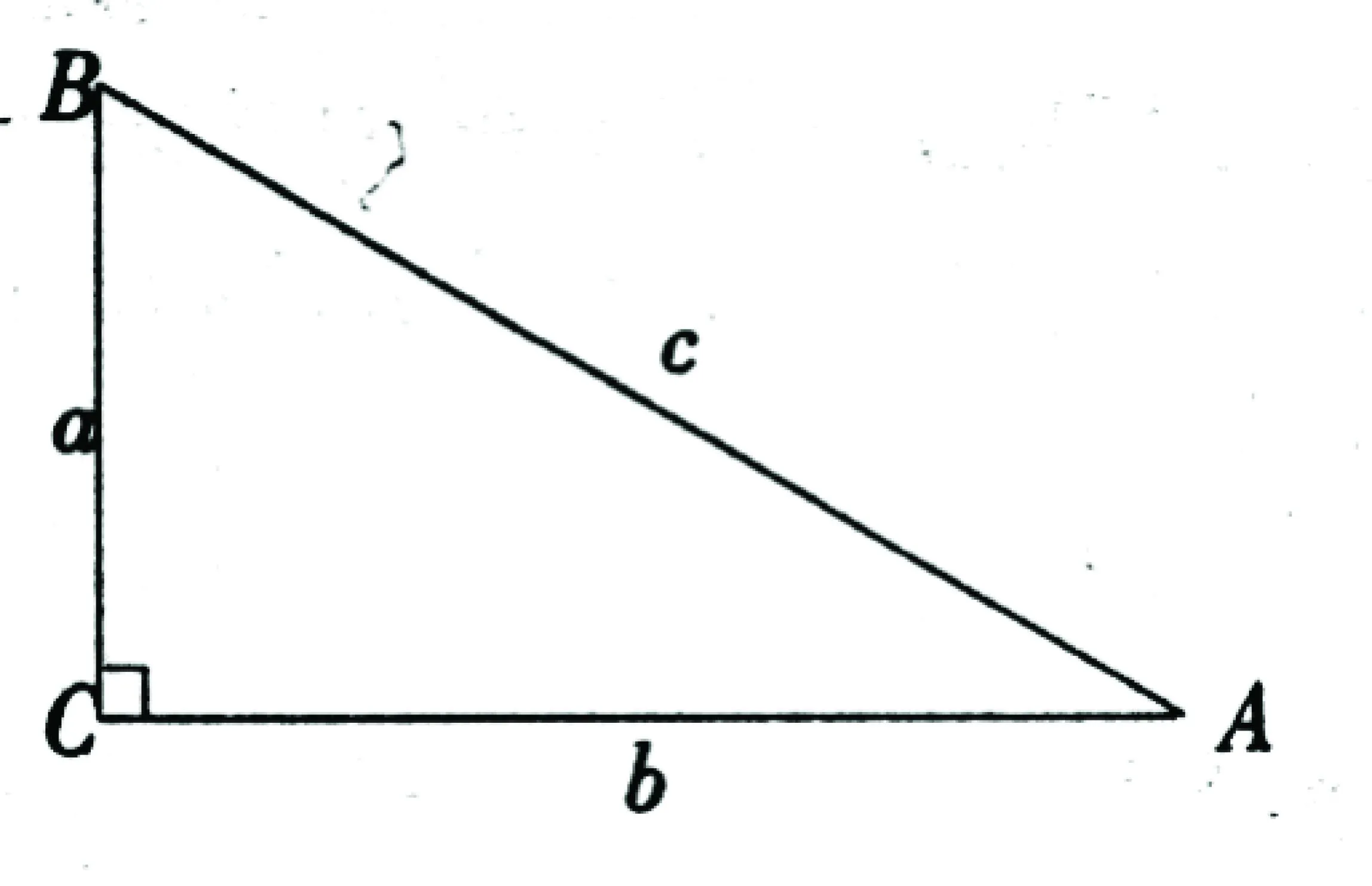
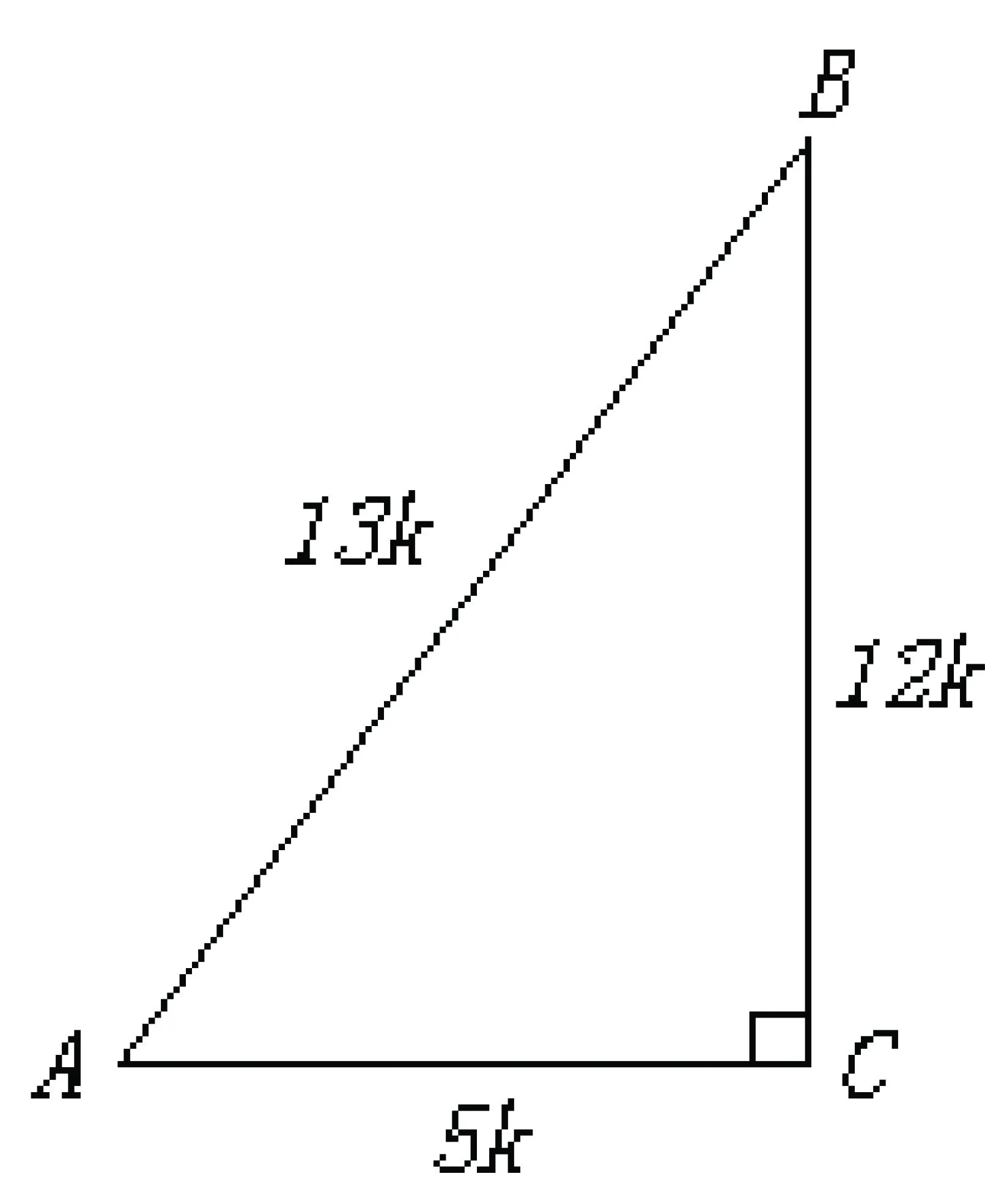
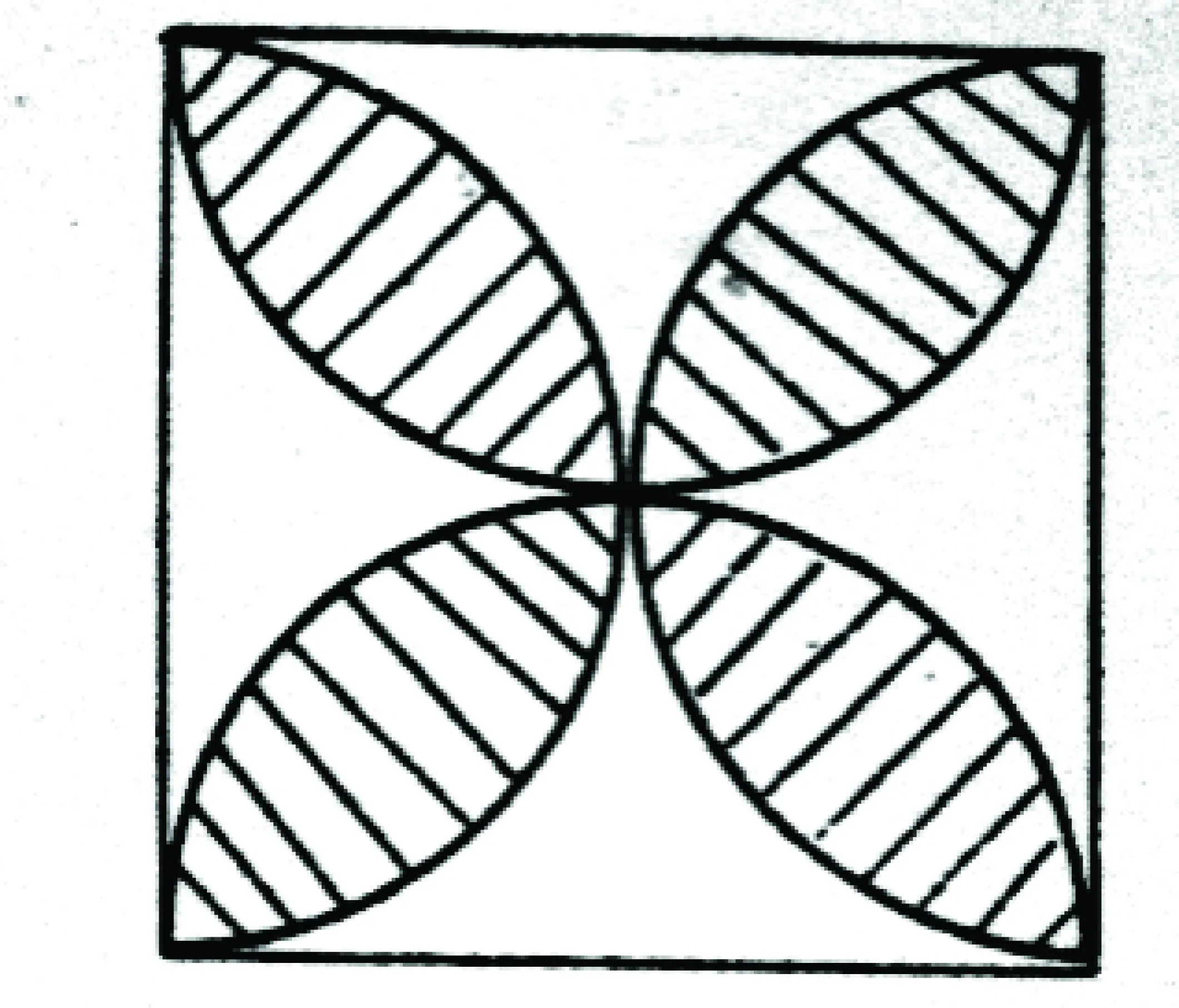
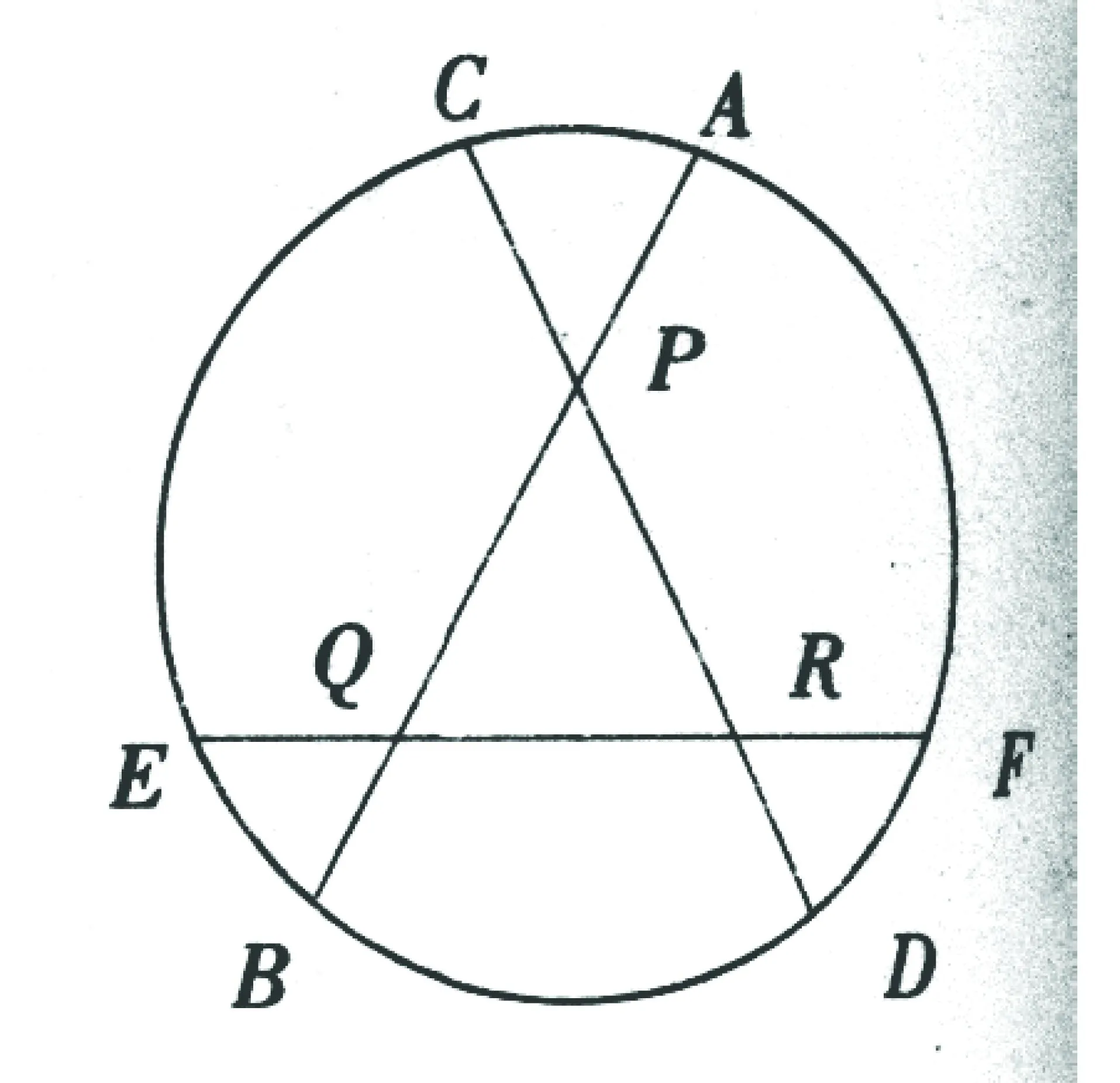
此题如果单从“数”的观点来思考，不易做对，但若与“形”(数轴)结合起来，就容易得多。由题意，在同一数轴上，找出一组分别表示a,-a,b,-b的点，如图：这样很快得出答案：b<-a

说明：借助数轴比较实数大小，直观，一目了然，且不易出错。

案例2：如图：已知a、b、c对应点在数轴上。

观察数轴：a>0，c-b>0 ，a+c>0。

易得：原式=a-(c-b)-(a+c)=b-2c

要确定不等式组的解集可借助数轴找出两个不等式解集的公共部分：

因此，不等式组的解集是1

这里a、b、b是直角三角形的三边，具有几何意义，如图(1)，由三角形三边关系定理：ac，c

因此，原式=-(a-b-c)+(a+b-c)+c-(c-a-b)=a+3b

图(1)

案例6：二次函数y=ax2+bx+c(a≠0)的图象如图(3)所示，试判定下列各式的正负：(1)a，(2)b，(3)c，(4)b2-4ac，(5)a+b+c，(6)a-b+c。

图(2)

图(3)

借助于函数图象来考虑：

(一)由抛物线开口向下，得a<0。

(三)由抛物线与y轴的交点知，x=0时，y=c>0。

(五)由抛物线与x轴的右边交点知：当x=1时，对应的抛物线上的点在x轴下方，所以，y=a+b+c<0。

(六)由抛物线与x轴左边的交点知：当x=-1时，对应的抛物线上的点在x轴上方，∴y=a-b+c>0。

三、由形思数，形数结合，用数解决形的问题

案例7：如图(4)，正方形边长为2，以各边长为直径在正方形内画半圆，求四个半圆所围成的图形(阴影部分)的面积。

图(4)

借助于面积公式求解：S阴影=4-2(4-π)=2π-4。

案例8：如图(5)，边长为1的正方形方格纸上，有A、B、C、D四个点。

图(5)

(一)求证：△ADC∽ △BDA；

(二)求∠ABD+∠BDA的度数。

(一)运用勾股定理“借数解形”

∴△ADC∽△BDA。

(二)由(1)△ADC∽△BDA

∴∠DAC =∠B

又∵∠DAC+∠ADB=45°

∴∠ABD+∠ADB=45°。

案例9：如图(6)，P为矩形ABCD内一点，已知PA=3，PB=4，PC=5，求PD的长。

图(6)

运用形数结合思想考虑。设点P到AD，AB的距离分别为x，y，BC=a，DC=b，依题意，得

(1)

(2)

(3)

案例10：如图(7)，已知⊙O中三弦AB、CD、EF两两相交于点P，Q、R，并且AP=EQ=RD，CP=QB=RF，求证：△RQP是等边三角形。

图(7)

四、结语

新课程改革到至今已近10年，中学数学课堂教学模式、教学方法发生了很大的变化，但万变不离其宗，数学本质的东西我们不能忽视，而且还要进一步重视，进一步加强。一名优秀的数学教师不仅要吃透教材中所规定必需掌握的知识点，而且要根据教材大纲的内容去整理提炼最重要的数学思想，并把这种解决问题的能力通过具体的知识点传授给学生，让学生在解题的过程中体会到高屋建瓴的审题技巧，能够把所有的数学思想串联起来融汇贯通，用辩证的思想解决看似复杂的问题，把问题简单化、具体化，直击难题的本质。这种能力的培养，不仅有助于学生在学习中培养正确的知识观念、建立解题的方法，而且有助于他们在以后的学习和工作中以一种正确观察获取信息的能力，面对学习和生活中的各种难题，做出正确的选择。

中图分类号：G633.6

文献标识码：A

文章编号：1006-0049-(2016)09-0184-02