如何基于目标生成的问题进行复习课教学——以“整数的复习”为例

◇游琼英

如何基于目标生成的问题进行复习课教学
——以“整数的复习”为例

◇游琼英

分享式教学倡导“问题、思考、分享”三个基本教学单元。在六年级下学期的总复习阶段，要把小学阶段所学的内容进行整理和复习，学生往往无从下手。怎么基于真问题开展复习课教学呢？我从北师大版教材六年级下册“整数的复习”入手进行了研究。

一 课前，学生完成复习单

为了帮助学生课前自主整理，我设计了“复习学力单”，包括“我的目标”“我的整理”“回顾反思”。“我的目标”概括了本次复习课的主要学习目标（知识和方法）；“我的整理”是让学生在读懂学习目标的基础上用问句来描述，引起学生的关注，并对核心问题进行重点整理，同时结合具体的例子复习相关的内容；“回顾反思”是对照问题看看哪些解决了，哪些还没有解决，是需要提出来研讨的。

“整数的复习”学力单

【我的目标】1.我能进一步理解整数的意义、表示方法等知识，回顾总结整数比较大小的方法，在估计大数、刻画数之间的相对大小关系等活动中发展数感。

2.我能回顾整理有关因数、倍数、质数、合数、奇数、偶数等概念，巩固求公因数、最大公因数、公倍数、最小公倍数的方法。

【我的整理】自学教材第65页。

1.根据学习目标，你认为复习整数应该弄清哪些问题？

2.关于倍数和因数,我们学了哪些内容？请选择合适的方式整理一下。

3.说一说下面这些数表示的意义。

（1）第1届奥运会于1896年在希腊雅典举行，2008年在北京举行的是第29届奥运会。

（2）长江是中国第一大河，流经11个省、直辖市、自治区。全长约6300千米，流域面积约180万平方千米。

（3）拉萨的区号是0891，面积约为31662平方千米，历史上最高气温是29.6℃，最低气温是零下16.5℃。2010年，常住人口约为56万人。

4.你能用尽可能多的方式表示2356吗？

方法1：（ ）；方法2：（ ）；方法3：（ ）。

5.举例说明怎样比较两个多位数的大小。

6.在小学阶段,你在哪些地方用到过0？说一说你对0的作用的认识。

7.举两个不同的例子,向同伴解释1万有多大、1亿有多大。

【回顾反思】对照提出的问题，我解决了哪些？还有什么困惑？

二 课中，学生基于目标生成问题进行探究与分享

（一）问题的生成。

1.读懂目标并提问。

师：请认真阅读学习目标，思考我们今天要解决哪些问题。

生:整数的意义是什么？

生:整数怎么表示和刻画？

生:怎么比较大小？

生:怎样估计大数？

生:因数、倍数、质数、合数、奇数、偶数的概念是什么？求公因数、最大公因数、公倍数、最小公倍数的方法是什么？

2.谈话聚焦大问题。

师：在这些问题中，你觉得哪个问题最开放、最具有挑战性？为什么？

生：第5个问题，因为这是复习阶段，重点内容应该是第5个问题。

生：我也赞成第5个，因为第5个问题的概念比较多，容易混淆，需要深入思考才知道，而且求公因数、最大公因数、公倍数、最小公倍数的方法很多、很开放。

师：那我们就先来探讨第5个问题。

(二)问题的探究和分享。

1.同伴互助先解决大问题。

师：课前，大家进行了自主整理。请四人小组相互看看，推荐一幅比较优秀的作品，在小组内补充完善，准备全班分享。

（第一组的生1出示图1）

图1

生1：因数和倍数，我首先介绍因数。比如3的因数有：1、3、2、1.5、等，所以因数可以有整数、小数和分数。

生：（评价）我反对，这里的因数和倍数是在非0自然数范围内的，因此这里的因数不能为小数和分数。

生1：我再来介绍倍数，倍数中有质数、合数。合数的因数个数比质数多。比如4是合数，因为4的因数除了1和4还有2，一共有三个因数。2是质数，只有1和2两个因数。

生2：（评价）我认为质数、合数不应该放在倍数这里，应该放在因数里。非0自然数是根据因数的个数来分的，质数只有1和它本身两个因数，合数除了1和它本身还有别的因数。还有1，既不是质数又不是合数。

师：还有哪些组跟他们不一样的？上来分享一下不一样的地方。

生2：（第二组）我的整理如下图（图2）。我首先整理什么是因数和倍数。如4×5=20，4和5叫20的因数，20是倍数。你们有什么补充和建议吗？

图2

生3：（补充）因数和倍数是相互依存的。不能说20是倍数，而要说20是4和5的倍数。

生2：然后我先说倍数，倍数的特征是，一个数的倍数的个数是无限的，其中最小的倍数是它本身，没有最大的倍数。2的倍数特征是，个位上是0、2、4、6、8的非0自然数；5的倍数特征是个位是0或5；3的倍数特征是各个数位上的数的和是3的倍数；6的倍数特征是各个数位上的数的和是3的倍数的偶数。你们有什么补充和建议？

生：（补充）9的倍数特征也是看各个数位上的数的和。

生2：因数的特征是，一个数的因数个数是有限的，其中最小的因数是1，最大的因数是它本身。非0自然数根据因数的个数可以分为质数、合数、1。大家有什么补充吗？

生：（评价）你的整理没有求最大公因数和最小公倍数的方法。

师：请你上来补充关于方法的整理。

生3：请看我整理的图（略），求最大公因数和最小公倍数的方法是短除法（如图3）。

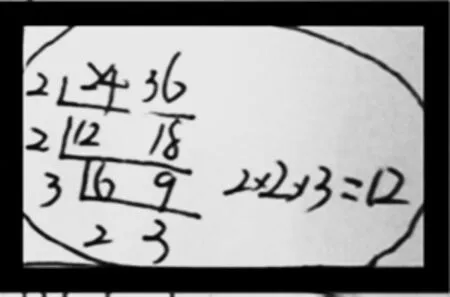
图3

生：（补充）还有互质关系的，如（8，9）=1，[8，9]=72；有倍数关系的，如（12，24）=12，[12，24]=24。

生3：也可以用大数翻倍法。如，36的1倍不是24的倍数，36的2倍是 72，72就是24的倍数。所以72是36和24的最小公倍数。

2.举例解决其他问题。

师：请借助课前的学力单，讨论解决剩下的问题。然后每组选1个问题重点解决。

（1）整数的意义是什么？

生1：我借助学力单的第3题，说说整数表示的意义（如图4）。

图4

师：其实整数的意义分为两类：一类主要是表示顺序，如第1届、第29届、1896年、2008年，我们称为序数；第二类主要是表示多少，如11个省、6300平方千米、180万平方千米、31662平方千米、29.6℃、零下16.5℃、56万人等中的数称为基数。

（2）怎么表示和刻画整数？

生2：请看下图（如图5）。方法1用计数器表示2356；方法2用扣子来表示，有2袋各装了1000颗，有3袋各装了100颗，有5袋各装了10颗，还有6颗单独的；方法3用钱来表示，有100元的23张，有10元的5张，还有5元和1元的各1张。

图5

生：（补充）还可以用下图表示（如图6）。

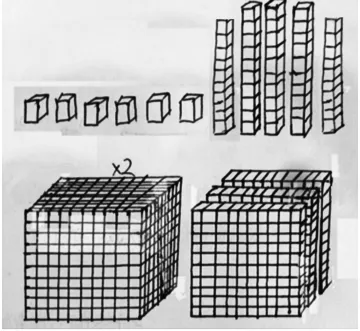
图6

（3）怎么估计大数？

师：举例，向同伴解释1万有多大、1亿有多大。

生1：如果每天吃10颗糖，那么1万颗糖大约吃33个月，也就是大约吃2年零9个月。

生2：1个矿泉水瓶子大约长20厘米，1亿个矿泉水瓶子首尾相接的长度大约能绕半个赤道。因为20×100000000÷100÷1000=2万（千米），赤道一周是4万多千米。

师：估计大数从身边的、熟悉的较小的数开始。

对于其他问题，学生没有提出来，就不用全班解决。

这节复习课也是围绕“问题、探究、分享”进行教学的，让学生根据目标提问，并通过排除法聚焦核心问题，而对于其他问题，则让学生结合例子来说明。

（作者单位：四川成都市泡桐树小学天府校区）