由一道练习题成就的一节模型思想建模课——“解决问题”教学实录与评析

执教/吴 媚 指导、评析/陈俊荣

由一道练习题成就的一节模型思想建模课
——“解决问题”教学实录与评析

执教/吴 媚 指导、评析/陈俊荣

【课前思考】

本节课的教学内容选自北师大版教材六年级上册“生活中的比”中的一道习题（如下图），在此基础上我们做了进一步的探究。

最初看到这道题的时候，我们认为只是一道简单的求比值的习题，得出“比值小的坡比较缓，比值大的坡比较陡”的结论。同时，我们又产生了质疑，陡不陡的结论在图上已经画得很明显了，学生一眼就能看出来，为什么教材中还要追问“你有什么发现”呢？随着对模型思想学习研究的深入，在寻找素材的过程中对这道题的疑问被逐渐解开了。

我们发现这道题绝不仅仅是浅层次的求比值练习，它是一个很好的数学模型的生活原型。如何体现其价值呢？我们以此为契机，带领学生经历了“质疑——学习——寻路——发现”的过程，才有了这节解决问题的建模课。

【教学实录】

师：请大家观察这两个水滑梯（如下图），如果让你玩儿的话，你会选哪个？为什么？

生：我会选择右边的滑梯，滑得快，刺激。

师：怎么设计滑梯才能滑得刺激呢？

生：陡的就刺激。

师：（板书：陡）看来，同学们对这种生活中的现象是有感受的，它可以用“陡”来描述。

（一）对生活中的“陡”进行科学的统一认识。

师：你们是怎么理解这个“陡”的？

（学生边示范边解释怎么样会更陡）

师：可以用胳膊比画。如果这就是“滑梯”，（比画）你能比画一个比我这个陡的吗？

（学生开始比画）

师：看来通过比画、描述，大家对“陡”有了共同的认识。

（二）在生活情境中分辨，找出比“陡”的方法。

师：刚才大家选右边的滑梯，是因为它比较陡，你是怎么比较出来的？

生：梯身短的滑梯陡。

生：我补充，同样高的时候，梯身短的陡。

师：看来只看一条边是不行的，要同时关注两条边。还有别的比较方法吗？

生：一样高时，水平距离越短的就越陡。

生：角度越大越陡。

师：你说的那个角在哪儿呢？

生：（指梯身与底面的夹角）这个角越大就会越陡。

（三）抽取模型。

师：在同学们的描述中有边又有角，有什么图形在你的脑中出现啦？

生：三角形。

师：你先想象一下这个三角形，然后动手画一画，再找一找这个图形和滑梯之间有什么联系。

（学生动手画三角形，教师请学生汇报画的图形，并画出三角形，如下图所示）

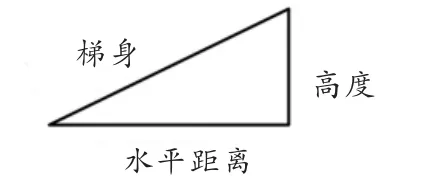
师：在比较两个滑梯哪个更陡的过程中，我们发现了三角形，并且在它和滑梯之间建立了联系。

（四）发现并解决数学问题。

1.画不同倾斜度的滑梯，尝试发现规律。

师：你能不能再画几个滑梯，让它们比这两个滑梯更陡呢？一边画一边观察，看看你会有什么发现。

（1）生独立动手画并观察。

（2）反馈汇报。 （如下图）

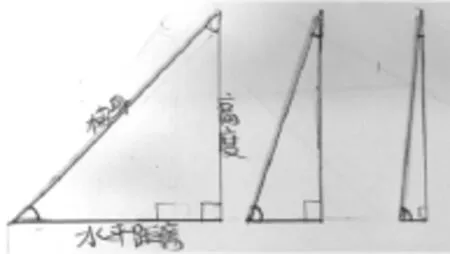
师：哪个滑梯比原来的陡？你有什么发现?

生：我整体观察了一下，滑梯倾斜度与角的变化是有联系的，与地面夹角越大，顶角就越小，梯身就越陡。

生：与边的变化也有联系，高不变时，斜边越短，底越短，滑梯就越陡。

师：我觉得大家很会思考问题，把滑梯的事儿变成了三角形的问题，不仅找到了方法，还有很多发现。

2.画出一样陡的滑梯，呈现关系。

师：老师也画了一个“滑梯”（如下图）,你能画出跟我这个一样陡的“滑梯”吗?

师：你们怎么不画呀？

生：没有数据。

师：你想要什么数据？又怎么得到数据？

生：量角度。

生：我没有量角器，还是画不了，我要量边。

（学生各自测量所需数据，测得底与斜边夹角约37°，高3厘米，底4厘米）

师：请你先把这个三角形画出来，再画一个和它一样陡的。画好后一定要告诉大家数据分别是多少。

（学生动手画，教师巡视，并组织学生进行汇报）

师：说说你是怎么画出来的。

生：我们以前学习过把角的两条边延长，角的大小不会变。所以我把37°角的两条边延长以后就能找到和它一样陡的了。（如下图）

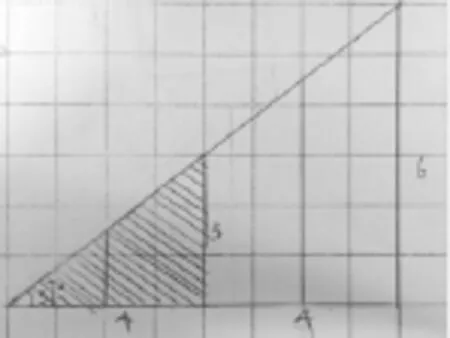
师：看来角的大小确定了，陡度就确定了。你得到一样陡的滑梯的数据分别是什么？

生：6、8、10与9、12、15。

师：把这几种情况（如下图）放在一起仔细观察，它们的边的长度、图形的大小都是变化的，那它们有什么共同点呢？生：它们的角度一样，边的比值也一样，都是。

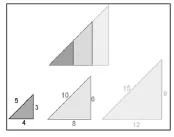
生：可以画无数个。

师：在我们解决陡不陡的问题时，我们不仅用比角、比边的方法，还换了个新的角度，从比边的关系入手，更准确地做出判断。当高与底的比值一样时，这些滑梯就一样陡，角度也就一样大。

（五）生活中的应用。

师：仔细观察下图，我们今天的研究在生活中有没有用处呢？

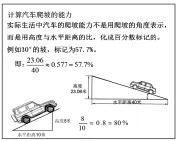
师：你能看懂吗？哪辆车的爬坡能力强？

生：越野车的爬坡能力强，因为它的爬坡高度与水平距离的比值大。

师：今天的学习对你有什么启发？

生：没想到小小滑梯中还藏着学问呢。

生：看似一个简单的三角形，却能帮助我们解决这么多问题。

师：（小结）回顾我们今天解决问题的过程，我们把生活中的滑梯问题转化成了数学中三角形的问题，找到了几种解决问题的方法，其中找关系的方法在生活中就有实际应用，你们的发现可真有价值。

【课后评析】

一道题一节课，从中可以看出教师的独具匠心。针对学生的已有知识和经验及学生发展性目标，恰当改造教材资源，依据学生的学习路径设计有效的教学活动，有条理地将新旧知识综合起来，使学生在自己原有认知的基础上有更进一步的认知和感悟。

模型思想是针对要解决的问题构造相应的数学模型,通过对数学模型的研究来解决实际问题的一种数学思想方法。本节课教学环节清晰、完整、具体,结合学生熟悉的生活，鼓励学生借助三角形来作为数学模型进行相关的研究，在收集、整理、筛选数据和确定研究方法的过程中，寻找方法间的联系，经历“生活情境——建立教学模型——解决问题——应用模型”的建模学习过程。

可以说，这是一节成功的建模课，不仅可以加深学生对比的认识，在解决实际问题的过程中帮助学生认识应用比的重要性，而且为学生到中学深入学习三角形的知识积累了经验，奠定了基础。

北京市海淀区中关村第三小学）