让学习真正发生——张齐华老师“用方向和距离确定位置”教学赏析

◇罗鸣亮

让学习真正发生
——张齐华老师“用方向和距离确定位置”教学赏析

◇罗鸣亮

近日，有幸聆听了特级教师张齐华执教的“用方向和距离确定位置”一课，简约大气的教学、以学生为本的课堂，彰显出其教学的智慧，折射出其深刻的教学思想。

一 简约教学，让课堂返璞归真

心理学家布鲁纳认为：任何学科的内容都可以用更经济、富有活力的简约方式表示出来，从而使学习者更容易掌握。一节课，如果赋予太多的东西，那么教学就会浮于表面，学生就无法深刻地把握知识本质。简约，不是简单，简化的是教学中细小琐碎的教学对话、繁杂的教学过程，留下的是形式上的简洁明了，方法上的深入浅出，活动中的专注思考、积极探索。

张齐华老师的课堂，简约朴素，于至简中见至真。

首先是简约的教学情境。“从数学学习的认知本质看,数学学习离不开情境；从数学课程及数学学习的特点看,情境化设计愈来愈显示出重要性和必要性。”但如果因“浓重的教育痕迹”或者“华丽、烦琐的再现”而失去其创设情境的目的，只能算一种教学虚假，对学生的人格培养和发展都是不利的。本节课，张老师仅用一个简单的情境“大海航行中的船只遇到故障，救援人员需要了解什么信息”，让学生产生解决问题的需要，于简单的情境中，激发学生迫切的学习需要，自然而然地进入新知教学环节。

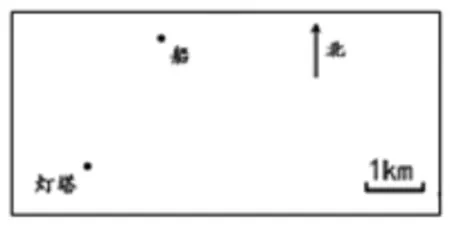
其次是简约的教学素材。形式多样、丰富多彩的素材虽能有效地激发学生学习的兴趣，但也容易造成学生在课堂上走马观花般迷失于 “美景”“好图”，反倒淡化了数学课堂思维训练的本质。张老师仅利用一张平面图（如下图）这一简单的素材，摈弃了船、灯塔等（实物）非知识本质的干扰，让学生的研究目的明确、针对性强。断出现的是 “还有别的方法吗”“谁来评价他的方法” “你有不同的想法吗”等诸如此类的语言，用这样简洁明了的语言让学生不断审视自己的思考过程，促进生生之间的互动交流，让学习逐步深入本质。正所谓“大道至简”，简约课堂是一种风格、一种气质、一种内涵，是洗尽铅华之后显素姿，是简单自然之中有深味。张老师课堂的简约，彰显的是教学的大气，拓展的是课堂学习的深度和广度。

二 自主探究，促认知层层深入

再次是简约的教学语言。张老师的教学语言之美是众所周知的，他的课堂总能达到一种“未成曲调先有情”的意境。而这节课，我们看到了他有意识地隐藏了自己的语言天赋，课堂上不

“有时回到原点，回到儿童，回到数学和教育的源头，也是一种超越，甚至是一种更具哲学意味的超越。”这是张老师在自我超越过程中提到的。在今天的课堂上，我们能够真切地看到：他真正做到了把课堂还给学生，让课堂从“教师的教”走向“学生的自主学习”。当学生发现新问题或产生新困惑时，教师并不急于给出答案，而是放手让学生合作和交流；学生能自己解决的问题，教师不教；当学生讲解不到位时，让其他学生帮忙补充完善。整个课堂呈现的都是学生交流、思考的过程。张老师以“退”促“进”，将学生推到了台上。

应该说，“确定位置”这一知识点对小学生而言是比较难以掌握的，因为需要综合运用比例尺、方向和量角等知识来精确地确定位置，特别是要让学生自主感受到距离、方向、角度对确定位置的必要性和准确性的确有一定难度。为此，在教学中借助平面图，围绕“如果以灯塔作为观测点，你能用数学的方法确定这艘船的准确位置吗”这一问题，让学生利用旧知“数对”解决问题时发现：数对虽然能反映船和灯塔的相互位置关系，但根据目前掌握的知识不能确定船究竟在哪里。学生在合作探究过程中，利用已有的经验，初步领悟到：灯塔到船的距离，就是两点之间线段的长度，可以根据比例尺来确定它的长度。

但是有了距离还是不能准确把握船的位置，如何让学生再进一步深入探究？张老师巧妙地让学生对这一方法进行评价，学生在评价中有了新发现，即光有距离是不够的，还得有具体的方位，由此唤起学生用已有的方位知识来表示船的位置。接着教师提出“看来有了距离、方位后，还缺了点什么”让学生深入思考，发现要精确确定船的位置还要准确描述其所在的角度，从而得出“方位、距离和角度，对于确定船的位置都很重要”。整个教学过程，学生在“要准确确定船的位置”这个问题的引领下，通过小组合作、同桌交流等方式，在不断的思维碰撞中感悟确定位置所必备的条件，让思考层层深入，最后豁然开朗。

三 数形结合，助思维走向深刻

平面直角坐标系作为代数和几何的纽带，承载着渗透数形结合的思想这一重任。作为图形与几何这一领域的内容，如何渗透数形结合思想？我们看到了张老师的深入研究及巧妙设计。在寻找船3的位置时，教师不再以常规方法给船找位置，而是分步提示。先出示提示1“船3在灯塔的南偏西方向”让学生猜猜：船3可能在哪儿呢？学生无法确定船3的位置，但是能指出船3所处的大致区域，也就是一个面。教师接着出示提示2“船3在灯塔的南偏西45°方向”，让学生把船3的位置比画出来。这时，学生比画出来的是一条线，从面到线，学生已经感受到随着条件的增加，确定船3位置的范围在逐渐缩小。

最后出示提示3“船3在灯塔的南偏西45°方向5千米处”。这下学生准确地找到了船3的位置。张老师借助图形的变化过程，让学生直观想象，感悟用距离和方向确定位置其实就是从面到线再到点不断精确的过程，把数形结合用到了极致。

四 对比联通，让知识回归本源

用数对确定位置与用距离和方向确定位置是小学阶段确定位置的两种方法，它们分别对应的是学生今后要学习的平面直角坐标系和极坐标系。这两种刻画位置的方法，既有不同点，又有相同点：都要有原点、坐标轴等组成的参照系；都要用两个要素来刻画位置。简单地说就是：要确定二维平面上一个点的位置，就必须用两个量才能确定。如何让学生自主联通这两种确定位置的方法，使得知识建构更为系统化？我们看到课的最后，张老师让学生把以前学过的数对和今天学习的方法比较一下，找出它们有什么不同，又有什么相似的地方。学生在对比中发现：两种方法都要用到两个量来确定位置。数对是用列数和行数确定位置，今天学习的则是用方向和距离两个量来确定位置。教师结合具体例题让学生发现：如果只给北偏东30°方向，那么船所在的位置在一条线上；如果只给3千米的距离，那么船所在的位置在一个圆内；圆和线相交的地方就是船所在的位置。而用数对表示，只给行数表示的是一条横线，只给列数表示的是一条竖线，两线相交的地方就是船所在的位置。这一过程让学生明确了，不管是哪种方法，都需要用两个量才能准确确定平面上的位置，沟通了两者之间的联系，回归本源处建立知识结构。

张老师的课堂，让我们再次领略到他从“教”到“学”的华丽转身，让我们感受到他对数学、儿童以及教学的思考在不断深入，这是他的又一次自我超越——逐步走向回归儿童、回归数学教育和教学本源的数学课堂！

福建省教研室）