大规模角点网格三维显示优化算法研究

2016-06-18崔书岳

中国石油大学胜利学院学报 2016年1期

关键词：个面角点数组

崔书岳

(中国石化石油勘探开发研究院,北京 100083)

大规模角点网格三维显示优化算法研究

崔书岳

(中国石化石油勘探开发研究院,北京 100083)

[摘要]角点网格是油藏地质建模和油藏数值模拟中常用的网格格式,对角点网格的数据结构进行详细分析,提出一种提高三维显示效率的算法。测试实例表明该算法可以将需要显示的网格体的面数降低到30%以下,显示时间降低到45%以下,证明该算法能有效提高角点网格的显示效率。

[关键词]角点网格;地质模型三维显示;OpenGL

在油藏的研究过程中,无论是油藏地质建模还是油藏数值模拟研究,地质体都是以网格的形式表述的[1],常用的有矩形网格、PEBI网格、径向网格、角点网格等。角点网格由Ponting引入油藏数值模拟[2],在地质建模和油藏数值模拟中得到了广泛应用,其格式得到了大多数建模软件和数值模拟软件的兼容。角点网格是一种结构化网格类型,网格位置能用i,j,k定义,并且单元网格的长、宽大小可变,垂向连接顶底网格点的网格面可以是倾斜的,能够更加精确地描述断层两翼的深度变化、流体分布和流体渗流特征[3]。基于角点网格的三维地质建模技术已经发展得比较成熟[4],采用角点网格系统开展油藏数值模拟研究的理论方法较为完善。近些年,精细油藏描述技术取得了很大进展[5]。油藏地质建模和数值模拟研究的尺度越来越细、网格规模越来越大,这对地质建模软件和数值模拟后处理软件中的三维显示提出了更高的要求。随着国内软件业的发展,越来越多的软件公司从事石油行业软件的开发工作,模型的三维显示是一项重要内容。笔者对角点网格的数据结构、顶点坐标计算进行详细分析,在此基础上提出一种提高角点网格显示效率的方法。

1角点网格的数据结构

角点网格通过垂向线和顶点深度来描述网格位置。在斯伦贝谢公司开发的油藏数值模拟软件Eclipse中垂线在COORD关键字中定义,顶点深度在ZCORN关键字中定义[7]。

假设一个模型在X、Y、Z方向上分别有NX、NY、NZ个网格(即共有NX×NY×NZ个网格),则共需要定义(NX+1)×(NY+1)条垂向线,所以COORD关键字部分共有(NX+1)×(NY+1)×6个浮点数。ZCORN部分定义了网格顶点的深度,每个网格有8个顶点,所以COORD关键字部分共有(NX+1)×(NY+1)×8个浮点数。

为更直观地说明角点网格的数据结构,以2×1×1(NX=2,NY=2,Nz=2)的网格为例说明COORD和ZCORN数据的存储顺序。COORD部分依次存储每条垂向线两个点的坐标,线的存储先后顺序如图1中线的编号(Li,i=1,2,3,4,5,6)所示。ZCORN部分依次存储网格的每个顶点深度,其存储顺序如图1中点的编号(Pi,i=1,2,…16)所示。

2角点网格绘制优化

2.1角点网格数据解析

角点网格的数据在文件中按上述顺序存储,在读取数据时建议采用一维数组的方式存储数据。这种方式实现简单,不需要进行其他条件的判断。文中定义COORD数据读取后存储在coord数组中,ZCORN数据存储在zcorn数组中。

确定模型中的每个网格需要4条垂向线的数据和8个顶点深度数据,如图2所示。

图1　角点网络数据库存储顺序示意图

第2条垂向线在数组coord中的开始位置为(j·(Nx+1)+i+1)·6。

第3条垂向线在数组coord中的开始位置为((j+1)·(Nx+1)+i)·6。

第4条垂向线在数组coord中的开始位置为((j+1)·(Nx+1)+i+1)·6,由此可从数组coord中提取出每条垂向线的顶点的坐标数据。

P1z在数组zcorn中的位置为:(k·Nx·Ny·8)+(j·Nx·4)+i·2,即:

P1z=zcorn[(k·Nx·Ny·8)+(j·Nx·4)+i·2]

同理可计算得出:

P2z=zcorn[(k·Nx·Ny·8)+(j·Nx·4)+i·2+1];

P3z=zcorn[(k·Nx·Ny·8)+(j·Nx·4+Nx·2)+

i·2];

P4z=zcorn[(k·Nx·Ny·8)+(j·Nx·4+Nx·2)+i·2+1];

P5z=zcorn[(k·Nx·Ny·8+Nx·Ny·4)+(j·Nx·4)+

i·2];

P6z=zcorn[(k·Nx·Ny·8+Nx·Ny·4)+(j·Nx·4)+i·2+1];

P7z=zcorn[(k·Nx·Ny·8+Nx·Ny·4)+(j·Nx·Ny·4+Nx·2)+i·2];

P8z=zcorn[(k·Nx·Ny·8+Nx·Ny·4)+(j·Nx·Ny·4+Nx·2)+i·2+1].

根据提取出的4条垂向线的端点数据和8个顶点的深度数据,可计算出该网格8个顶点的(x,y)坐标,即

其中i为该网格垂向线和顶点深度数据的序号。计算出网格的顶点坐标后就可以进行网格绘制了。

2.2角点网格绘制

OpenGL作为一种与平台无关的三维程序开发接口[7]以其良好的性能和丰富的基本操作函数在三维可视化领域得到了广泛的应用[8-10],几乎所有的计算机编程语言都能很方便地对其进行调用。本文使用OpenGL实现了角点网格和油藏属性数据的显示。

在使用角点网格的油藏数值模拟输入文件中,网格部分以角点网格的结构存储;油藏属性数据(如孔隙度、渗透率)则是按网格位置(第i行,第j列,第k层)循环的方式存储的。根据上面的描述,网格的顶点数据也是可以通过i、j、k的方式计算,所以在绘制的时候可以采取i、j、k循环的方式对每个网格进行绘制。这样网格的几何结构与其属性数据就有了直接的对应关系,便于网格的着色。

假设现在需要对地质模型的孔隙度场进行三维显示。孔隙度属性值存储在一维数组poro中,则处于第i行、第j列、第k层的网格的孔隙度的值为

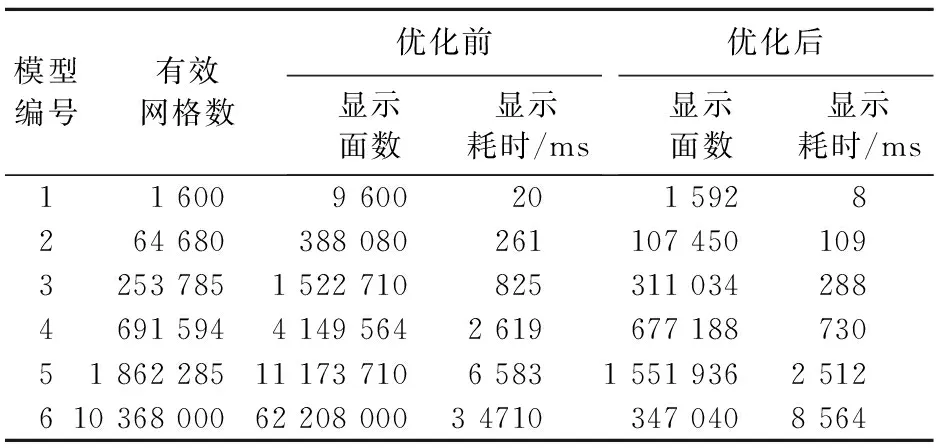
cporo=poro[k·Nx·Ny+j·Nx+i],0≤i

绘制三维模型的程序可以描述为:

Fork=0toNz-1

Forj=0toNy-1

Fori=0toNx-1

计算网格顶点坐标;

读取孔隙度值;

计算孔隙度对应的颜色值;

绘制网格的六个面;

Endi;

Endj;

Endk;

通过上面的描述,可以实现地质属性场的三维显示。当地质模型网格数量很大时显示效果很差,图形的旋转、拖动等操作变得非常慢,极大地影响了程序的用户体验。为提高三维显示的效率,本文中设计一个优化算法来判断哪些网格面需要显示。

算法的基本思想是在绘制之前先生成一个网格绘制标示数组gridstatus,并初始化为0,用来记录网格的每个面是否需要绘制。为与网格系统一致,设gridstatus为一个三维数组,其类型可以是Btye或整型(根据使用的语言而定,本文中以整型为例)。处于第i行、第j列、第k层的网格gk,j,i的显示状态值为gridstatus[k,j,i]。

用gridstatus[k,j,i]低六位来记录网格的6个面是否需要显示,网格面的编号如图3所示。

图3　网络面编号

根据角点网格的数据定义方式可知,网格gk,j,i的面3与其 “前方(X方向)”网格gk,j,i+1的面4相邻,两个面是否重合只需对网格gk,j,i的深度数据P2、P4、P6、P8(图2中的编号)是否与gk,j,i+1的深度数据P1、P3、P5、P7(图2中的编号)分别相等即可;判断网格gk,j,i的面6是否与其“右方(Y方向)”网格gk,j+1,i的面5重合,需要判断网格gk,j,i的深度数据P3、P4、P7、P8(图2中的编号)是否分别与网格gk,j+1,i的深度数据P1、P2、P5、P6(图2中的编号)相等;判断网格gk,j,i的面2是否与其“下方(Z方向)”网格gk+1,j,i的面1重合,需要判断网格gk,j,i的深度数据P1、P2、P3、P4(图2中的编号)是否分别与网格gk+1,j,i的深度数据P5、P6、P7、P8(图2中的编号)相等。如果两个相邻网格面的对应数据都分别相等,说明两个相邻网格面是完全重合的,此时这两个面都不需要绘制;否则，两个面都需要绘制(如有垂向断距断层两侧的网格)。

根据上述分析,网格gk,j,i的每个面的显示与否的判断原则表述为:

如果网格gk,j,i的面2与网格gk+1,j,i的面1重合,则网格gk,j,i的面2与网格gk+1,j,i的面1不需要绘制;否则这两个面都需要绘制,此时令

gridstatus[k,j,i]=gridstatus[k,j,i]+1,

gridstatus[k+1,j,i]=gridstatus[k+1,j,i]+2.

如果网格gk,j,i的面3与网格gk,j,i+1的面4重合,则网格gk,j,i的面3及网格gk,j,i+1的面4不需要绘制;否则这两个面都需要绘制,此时令

gridstatus[k,j,i]=gridstatus[k,j,i]+4,

gridstatus[k,j,i+1]=gridstatus[k,j,i+1]+8

如果网格gk,j,i的面6是网格gk+1,j,i的面5重合,则网格gk,j,i的面6是网格gk+1,j,i的面5不需要绘制;否则这两个面都需要绘制,此时令

gridstatus[k,j,i]=gridstatus[k,j,i]+16,

gridstatus[k+1,j,i]=gridstatus[k+1,j,i]+32

以此原则,可以计算出每个网格每个面的显示状态值。计算时可以从第0层第0行开始,只需将当前网格面与其“前(X方向)、右(Y方向)、下(Z方向)”向的网格面进行判断即可。如果其一个方向上的下一个网格为死网格或是边界,则该网格的当前面也需要显示。

gridstatus计算的程序描述为:

//根据过滤条件设置网格是否为要显示的网格

Fork=0 toNz-1

Forj=0 toNy-1

Fori=0 toNx-1

如果为死网格或不符合显示条件的网格,

令gridstatus[k,j,i]=0

否则令:gridstatus[k,j,i]=64

Endi;

Endj;

Endk;

//网格面是否需要绘制判断

Fork=0 toNz-1

Forj=0 toNy-1

Fori=0 toNx-1

如果网格gk,j,i为死网格或不符合显示条件的网格,跳出此次循环;

网格gk,j,i是否为边界网格判断,如果是边界网格,根据方向设置边界面的gridstatus值;

计算网格gk,j,i的深度数据;

根据前述原则判断相邻面是否需要显示,并设置gridstatus值;

Endi;

Endj;

Endk;

gridstatus的元素赋值后,绘制网格时就可根据其中的值来判断哪些面需要绘制,哪些面可以“省略”。以孔隙度属性显示为例，程序可以描述为:

Fork=0toNz-1

Forj=0toNy-1

Fori=0toNx-1

计算网格顶点坐标;

读取孔隙度值;

读取网格面显示状态值,

cstatus=gridstatus[k,j,i];

计算孔隙度对应的颜色值;

if(cstatus&& 1=true) 绘制面1;

if(cstatus&& 2=true) 绘制面2;

if(cstatus&& 4=true) 绘制面3;

if(cstatus&& 8=true) 绘制面4;

if(cstatus&& 16=true) 绘制面5;

if(cstatus&& 32=true) 绘制面6;

Endi;

Endj;

Endk;

这种方法不仅减少了面的绘制数量,而且能自然地处理断层、镂空显示。实际应用中条件过滤等操作均可以通过改变该数组来实现。

3实例

测试例1,模型网格总数为1 600, 有效网格数为1 600。如果每个网格的6个面都显示,需要绘制9 600个面,绘制时间为20 ms;使用本文的算法处理后,只需绘制1 592个面,是优化前的16.58%,绘制时间为8 ms,是优化前的40%,模型中的断层显示正常。

测试例2,模型网格总数为66 960,有效网格数为64 680。优化前需要绘制388 080个面,优化后需绘制107 450个面,是优化前的27.69%;优化前绘制时间为261 ms,优化后需要109 ms,为优化前的41.76%,模型镂空显示正常。

测试例3,模型网格总数为925 740,有效网格数为253 785。优化前需要绘制1 522 710个面,优化后只需绘制311 034个面,是优化前的20.43%;优化前绘制时间为825 ms,优化后需要288 ms,为优化前的34.91%。

测试例4,模型网格总数为2 371 881,有效网格数为691 594。优化前需要绘制4 149 564个面,优化后只需绘制677 188个面,是优化前的16.32%;优化前绘制时间为2 619 ms,优化后需要730 ms,为优化前的27.87%。

测试例5,模型网格总数为6 241 020,有效网格数为1 862 285。优化前需要绘制11 173 710个面,优化后只需绘制1 551 936个面,是优化前的13.89%;优化前绘制时间为6 583 ms,优化后需要2512 ms,为优化前的38.16%。

测试例6,模型网格总数为10 368 000,有效网格数为10 368 000。优化前需要绘制62 208 000个面,优化后只需绘制347 040个面,是优化前的0.56%;优化前绘制时间为34 710 ms,优化后需要8 564 ms,为优化前的24.67%。

6个测试模型的数据如表1所示,显示面数的优化效率与显示时间效率如图4所示。

表1　测试模型数据表

图4　显示面数与显示时间效率

测试环境:

处理器:Intel(R) Core(TM) Quad CPU Q9400 @2.66 GHz 2.67 GHz;

内存:3.25 GB;

系统类型:32位操作系统(WIN7);

显卡:NVIDIA GeForce 9300 GE,显存:256 MB。

4结束语

本文中详细介绍了角点网格的数据结构,并根据数据存储的特点给出了一维数组格式下网格顶点坐标的计算方法,该方法给出了角点网格数据与网格所在层、行、列序号之间的对应关系,便于三维显示。提出了减少网格显示面的算法,算法采用设置网格面显示状态数组的方法减少了需要显示的网格面数,提高了显示效率。

[参考文献]

[1]吴胜和,金振奎.储层建模[M].北京:石油工业出版社,1999.

[2]PONTING D K, Corner point geometry in reservoir simulation: proceedings of first european conference on the mathematics of oil recovery[C]. Oxford: Clarendon Press,1992:45- 65.

[3]韩峻,施法中,范峥,等.基于格架模型的角点网格生成算法[J].计算机工程,2008,34(4):90-92.

[4]刘志峰,魏振华,吴冲龙,等.基于角点网格模型的“迷宫式”油气运聚模拟研究[J].石油实验地质,2010,32(6):596-599.

[5]惠钢.精细油藏描述技术现状及发展趋势[J].四川地质学报,2012,32(1):66-68.

[6]Eclipse Reference Manual[Z].Schlumberger,2006:454,2266.

[7]EDWARD A. OpenGL 程序设计指南[M].李桂琼,张文祥,译.北京:清华大学出版社,2005.

[8]陈举民,王新峰,卫文彧,等.油藏数值模拟中的网格技术应用概述[J].中国科技博览,2010(22):2-3.

[9]毛小平,张志庭,钱真. 用角点网格模型表达地质模型的剖析及在油气成藏过程模拟中的应用[J].地质学刊,2012,36(3): 265-273.

[10]李芳玉,陈传波,钟宝荣.基于OpenGL的地层模型三维可视化图形显示方法[J].江汉石油学院学报,2001,23(1):20-21.

[责任编辑]王艳丽

[收稿日期]2015-12-20

[作者简介]崔书岳(1979—),男，山东德州人，中国石化石油勘探开发研究院工程师，主要从事油藏数值模拟研究。

doi:10.3969/j.issn.1673-5935.2016.01.009