浅水方程大规模并行计算模拟城市洪水演进

许 栋，PAyet David，及春宁，徐 彬，白玉川，刘红波

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 上海交通大学高新船舶开发装备协同创新中心，上海 200240；3. 天津大学建筑工程学院，天津 300072）



浅水方程大规模并行计算模拟城市洪水演进

许 栋1 2，PAyet David3，及春宁1，徐 彬1，白玉川1，刘红波1

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 上海交通大学高新船舶开发装备协同创新中心，上海 200240；3. 天津大学建筑工程学院，天津 300072）

摘要：基于有限体积法建立求解溃坝水流运动的数学模型，利用Riemann问题求解Godunov格式计算通量，通过空间分块划分的大规模并行计算来加速运算，实现了城市洪水演进的精细数值模拟.数值模拟结果表明，建筑物在溃坝波波前到达初期所受水流荷载最大；受上游建筑物消波、蔽护作用，溃口下游建筑物所受荷载随至溃口的距离的增大而减小，建筑物的存在使得溃坝波在城区传播速度减慢.并行测试表明，缓冲模式比非缓冲模式更适用于浅水方程大规模并行求解.目前大规模并行计算能够实现对面积达400 km2的城区洪水演进进行实时仿真模拟，为滨河、滨海城市在受到溃坝、海啸等洪水威胁时的快速决策和应急疏散提供科学依据.

关键词：洪水；浅水方程；溃坝；并行计算

洪水灾害是威胁现代化城市安全的重大自然灾害之一，洪水波演进速度快，遇障碍物后产生反射、绕射和散射［1-2］，并形成强大冲击荷载，严重威胁城市建筑物安全.我国目前建有大量不同等级的水库堤坝，水位落差在几十米至上百米之间，对于水库下游城市，堤坝失事后的溃坝洪水威胁不容忽视［3-5］.另一类较常见洪水来自海啸，海底地震引发的波浪在海洋中传播到达海岸后，发生浅水变形，形成数米甚至10 m以上的浪墙，对沿岸城市形成极大威胁.例如，2011年3月11日日本本州东北部海域发生Mw9.0地震，诱发的海啸侵袭了沿岸城镇［6］.近年来由HR Wallingford等9所研究机构联合执行欧盟IMPACT［7］研究计划，系统评估了洪水对城市建筑的威胁.进行城市洪水演进仿真模拟，对于城市灾害预报预警以及应急预案编制具有重要科学意义.

城市洪水模拟比河流洪水更为复杂，主要体现在以下方面.首先，城市中往往有密集分布的建筑物，形成洪水演进的反射、绕射、散射或淹没，成为复杂的水流动边界，这些动边界的识别与跟踪对数值模拟提出了很高的要求.例如，张大伟等［5］通过考虑社区和楼房内部的容水性，创新性地引入侵入水量的概念，建立了能够模拟建筑物密集城区溃堤水流运动的数学模型；其次，河道洪水模拟一般计算域狭长，可以根据河道走向采用一维、一维二维耦合或拉伸网格的二维模拟，减小计算量，而城市区域往往不存在优先方向，必须全域采用二维模拟；再次，河流洪水传播时间一般长达数小时以上，而在城市区域传播往往不足1 h，为在洪水发生后应急响应，对数值模拟计算效率提出更高要求.

基于大规模并行计算的数值模拟是解决上述计算量和计算效率矛盾的有效手段.随着计算机技术的发展，并行计算越来越多地被应用于浅水方程求解.江春波等［8］采用信息传递接口（MPI）通讯库，实现了基于图论的区域剖分方法，用于浅水方程并行求解.李铁键等［9］探讨了集群计算在数字流域模型中的应用.周洋等［10］针对模拟潮汐流动的浅水方程采用OpenMP进行了并行化研究.近年来还有基于GPU并行技术的求解浅水方程的尝试.这些研究工作多侧重于基本原理构建，一般规模较小，并采用概化地形，针对复杂城区的大规模水流模拟目前鲜有开展，实际应用效果有待论证.

目前地理信息系统已能够提供分辨率达0.5 m的城区三维数字地形，足以刻画城市建筑物的分布细节.在这样的背景下，本文建立浅水方程大规模并行计算模式，并针对复杂的虚拟城市地形进行模拟，研究了溃坝洪水在三维城市中的演进规律.

1　控制方程及数值求解

1.1洪水运动的二维浅水方程

洪水运动利用二维浅水方程进行描述，包括连续性方程和沿x、y两个不同方向的动量方程，可以概况为以下向量方程形式，即

式中：q为待求变量矩阵；h为水深；u、v分别为沿x、y方向的速度分量；b为地形高度；g为重力加速度；Sb x、Sb y分别为沿x、y方向的地形梯度；Sf x、Sf y分别为沿x、y方向的底部摩阻，可以利用曼宁公式计算，即

式中n为曼宁阻力系数.

1.2数值离散及求解

利用有限体积法对控制方程进行离散.为方便并行程序设计，采用结构化网格.所求解变量qij定义在控制体中心（见图1），控制体Ωij（i，j为单元编号，Ωij指图2中阴影部分）的状态由变量qij所描述，沿x方向通量E和沿y方向通量G定义在网格边界上.

图1　有限体积法控制体示意Fig.1 Schematic of control volume for finite volume method

控制体内在时间tn至tn+1内的通量增量可通过控制体积分计算，即

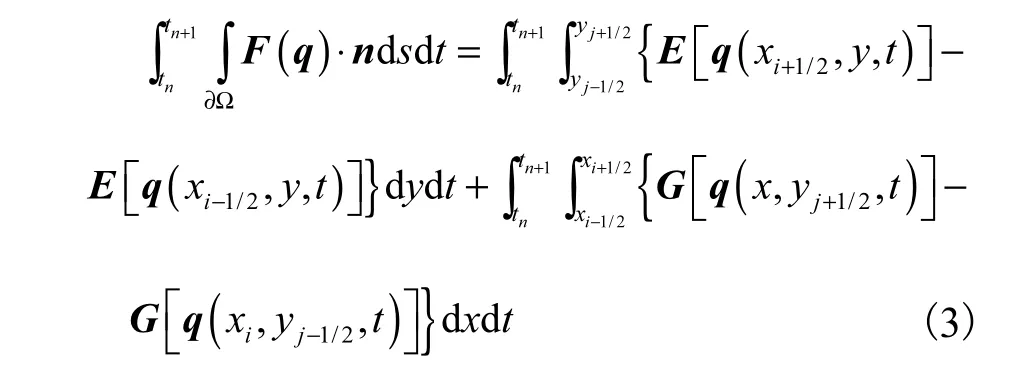
通量构建是有限体积法求解的关键.为适应溃坝水流强间断的特征，本文采用基于Riemann求解器的Godunov格式计算界面通量，详细格式见文献［1-2］.为方便描述时间计算格式，定义控制体积分量，采用显示欧拉时间格式

1.3动边界处理

采用干湿判断方法进行动边界处理［11］，为避免数值振荡，将动边界处理分为干判断和湿判断两个过程［12］.具体地讲，当单元预测水深h＜hdry时干出，该单元不参与计算；当单元预测水深h＞hwet时，单元重新变“湿”，恢复参与计算；hdry和hwet分别是干判断和湿判断的容差，为保持数值稳定，一般设定hwet＞hdry.

2　基于空间划分的并行计算

本文采用空间分块划分并行策略，这种方法简单易行且并行效率极高，在计算流体力学中具有大量成功的应用［13-14］，适用于大规模并行计算任务.如图2所示，每个块（block）的有效计算域为nx×ny，为了计算边界单元通量，需要在此区域外设置一层虚拟网格（ghost layer），因此最终采用块大小为nx×ny.考虑到共享内存并行计算（如OpenMP）规模受节点限制，不适于城市洪水模拟，本文采用基于消息传递界面（message passing interface，MPI）的分布式内存并行方式，并提出两种不同的并行模式：非缓冲和缓冲模式.非缓冲模式在每个时间步计算完成后，在不同块间直接交换边界网格数据，然后各块同步，并进入下一时间步计算，见图2（a）.由于在大规模并行计算中，频繁的、小粒度数据交换严重制约并行效率，本文采用缓冲技术改善这一问题.

缓冲的并行模式具体实施方法为在各计算节点缓冲区内分别建立两个数据队列：当地队列和远程队列，见图2（b），数据交换按以下步骤（以x方向为例）进行：①各块将边界单元数据（i=1 及i=nx处的h，u，v等）利用MPI_Pack函数打包压缩并放入当地队列；②不同节点间利用MPI_Isend和MPI_Recv函数同步进行数据交换，接收对方发来的打包数据并放入远程队列；③各块从接收到的远程队列中读取数据并利用MPI_Unpack函数对数据进行解压；④将解压后数据写入本块虚拟网格层中；⑤各节点进入下一时间步计算.在上述处理过程中，数据队列构建、打包处理增大了数据交换粒度，加速了数据交换；另一方面，通过非阻塞通信模拟（MPI_Isend实现），使得进程在与另一个进程通信的同时继续参与计算，进一步提高并行效率.对于上述两种并行模式的运行效率，将在案例计算中进行测试比较.

图2　空间分块并行计算示意Fig.2 Schematic of spatial decomposition with blocks

3　数学模型验证

采用两组数据对本文所建立数学模型进行验证.第1组为溃坝水流，采用经典的解析解作为验证依据. 考虑一维瞬间溃坝问题，计算域长度为1 000 m，溃口位于x=500 m处，初始时刻上游水深为10 m，下游水深为2 m.数值模拟采用网格dx=1 m，溃坝发生30 s后的水面线比较如图3（a）所示.从图中可以看出，本模型计算结果精度与Liang等［15］的模拟大致相同，与解析解符合较好，证明目前采用的数值计算格式能够很好地捕捉溃坝水流间断特征.另外针对不同网格尺寸进行测试，网格分辨率对模拟结果的影响如图3（b）所示.从图中可以看出，当网格尺寸小于4 m时，均能获得较高精度的模拟结果.

图3　溃坝水流数学模型验证Fig.3 Verification of mathematical model using dambreak flow

为验证非平底、动边界情况下，数学模型对干湿判断的计算精度，第2组验证采用抛物型浅水湖中的自由面震荡算例.Thacker［16］通过推导得出了抛物型浅水湖中的自由面震荡问题的解析解，被很多学者用来验证动边界处理方法的效果［17］.本文选用的算例参数与Zhao等［17］相同，静水水面半径R= 2 500 m，初始中心水深为h=1 m，其他参数详见文献［18］.数值模拟在水面振荡半个周期（T/2）后的水面见图4（a），模拟结果与解析解符合较好，见图4（b）.说明本文所采用的干湿判断能够有效处理动边界问题.

图4　抛物型浅水湖中自由面震荡验证Fig.4 Verification using free surface oscillation in a parabolic lake

4　城市洪水演进模拟

4.1虚拟城市构建

为了验证所建模型对建筑物密集的城市区域洪水演进模拟的效果，测试大规模并行计算加速的可行性，同时研究建筑物对洪水传播的影响机制，本文针对一个虚拟构建的城市区域进行水流数值模拟.随着地理信息系统的不断发展，虚拟城市技术、三维城市建模（3 DCM）技术近年来发展迅速，能够对城市进行多分辨率、多尺度、多时空和多种类型的三维描述，用于模拟和表达城市地形地貌、建筑物布局等.这些技术能够为水流数值计算提供必要的边界条件及基础数据支持.为方便起见，本文将建筑概化为随机放置在平整地面上的大量长方体障碍物，其长度和宽度为［20 m，100 m］之间的随机数，高度为［3 m，28 m］之间的随机数.计算域为长7 680 m、宽1 536 m的矩形区域，共随机生成建筑物100座，生成的三维城市地形如图5所示.建筑物平面面积共3.6万m2，占城区总面积的4.13% .

4.2计算网格及参数

在x、y两个方向均采用间距1 m的均匀网格.从图3（b）中的网格精度测试结果来看，间距4 m的网格已能够较好地模拟溃坝水流运动，然而考虑到城市区域不同大小建筑物密集，为获得足够的空间分辨率，采用1 m边长的正方形网格，见图5.实际上针对1 m分辨率网格的城市数字高程（DEM）数据目前已能够利用遥感等技术获取.本算例网格总数为7 680×1 536=11 796 480，约为1 180万.为便于并行计算，将整个区域划分为60×12=720块，如图6所示. 每个计算块包含128×128=16 384个计算网格.

边界条件设置为：左侧为入流边界，设定水位H=20 m，右侧为自由出流边界，上下边界采用周期性边界条件，需要在每个计算步后显式交换边界信息.水库位于左侧x＜2 000 m的区域，初始水位为20 m；右侧为城区，初始为干底.主要计算参数如表1所示.

图5　三维城市地形整体及局部细节Fig.5 Overall and details of three-dimensional city topography

图6　计算区域空间分块及边界条件Fig.6 Spatial block decomposition of computational domain and boundary conditions

表1　主要计算参数Fab.1 Major computational configurations

4.3数值模拟结果

数值计算获得的洪水在城市中传播过程仿真结果如图7所示.从图中可以看出，本文所建立的数学模型能够很好地反映溃坝洪水在建筑物密集的城区的传播，能够捕捉溃坝波在建筑物前的水位壅高、水波反射、绕射和散射以及低矮建筑淹没过程等细节.在绕流建筑物的后方，如图7（b）中的区域2，有较狭长的低流速区（u＜1 m/s），且有形如卡门涡街的漩涡脱落.建筑物两侧为高流速区（u＞5 m/s）.溃坝水流流过整个城区（长度为5 680 m）需时约1 400 s.

为了更清楚地观察建筑物绕流及淹没的细节过程，从图7中取区域 1放大，如图8所示.其中图8（a）、（b）为建筑物B1的绕流过程，可以看出水流在到达建筑物后，在前方（迎流面）形成约1 m高的水位壅高，并发生溃坝波的反射和绕流.图8（c）、（d）为建筑物B2的淹没过程，该过程伴随向前移动的动态水边界，通过数值模拟中的干湿判断进行处理.从图中还可以看出，在溃坝波到达建筑迎流面初期，建筑物受静水压强和动水冲击（动压）荷载共同作用，产生较大的后倾力矩；而在完全淹没或绕流发生后，建筑物前后水位差变小，此时建筑物主要受动压作用，失效风险降低.

在图6中取代表性建筑物A、B、C，提取不同建筑物前后的水位过程如图9所示.同一时刻水位前后水位差反映建筑物所受水流静水压力作用.从图中可以看出，位于下游位置的建筑物（建筑 C）由于受到上游建筑物的蔽护以及消波作用，其所受水流冲击速度与建筑 A相比，减小约50% .将所有的建筑物去除，进行下游平底情况的溃坝水流模拟，并将沿宽度平均的瞬时水面线与上述城市区域结果进行比较，见图10.从图中可以看出，由于建筑物的存在，使得溃坝波在城区传播速度比平底情况减慢3.6% .鉴于实际城市中建筑物对洪水演进的影响受建筑物密度、形态、排列方式等多种因素共同制约，具体的影响程度需要通过更多系统地模拟和分析确定.

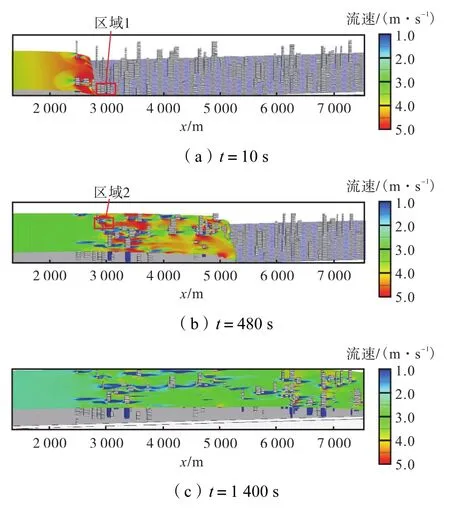
图7　洪水在城市中传播的仿真结果Fig.7 Simulation results of flood propagation in urban areas

图8　建筑物溃坝水流绕流及淹没Fig.8 Dam-break flow surrounding buildings and building submergence

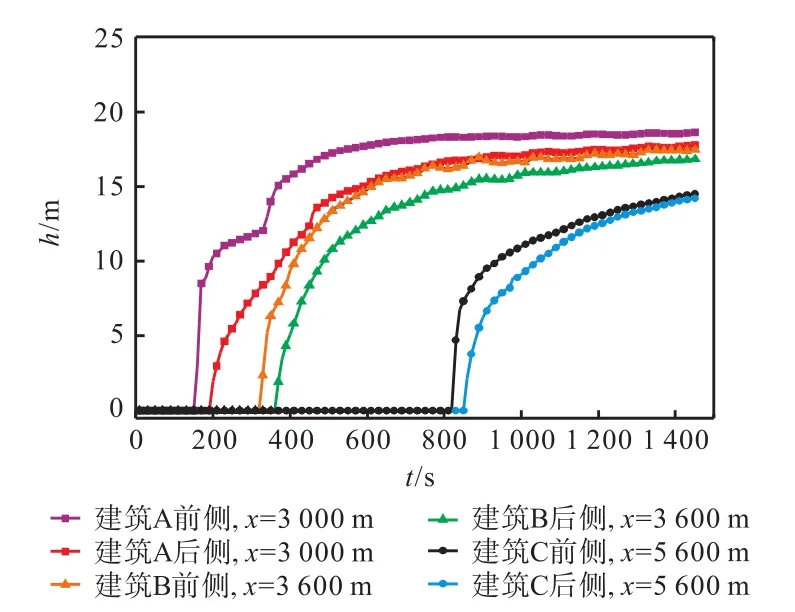
图9　不同建筑物前后的水位过程Fig.9 History of water level in front of and at the back of different buildings

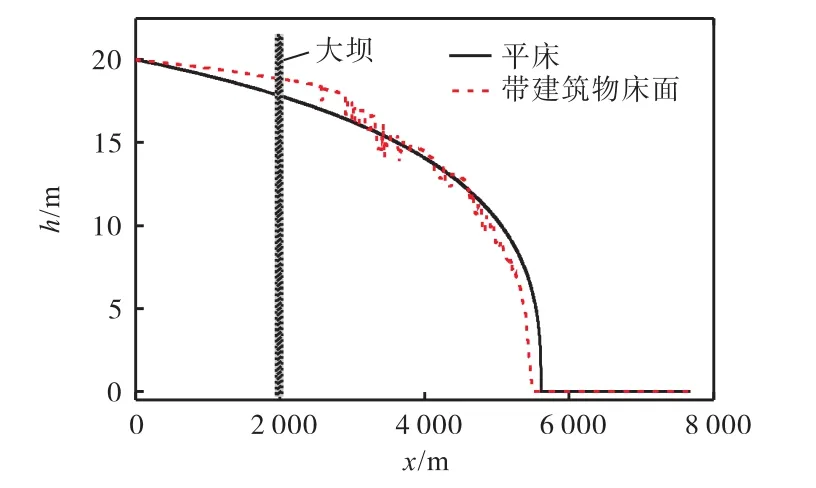
图10　平底与非平底溃坝瞬时水面线比较（t=800 s）Fig.10 Water level comparison for dam-break flow with flat and non-flat beds（t=800 s）

4.4并行效率讨论

上述数值计算程序采用Linux系统下C语言编写，使用gcc+mpich2编译，在大型并行计算集群上运行.节点硬件为Dual Quad-core Xeon（E5420）处理器，主频为2.50 GHz，节点通讯采用DDR Infiniband连接.为了测试程序并行效率，代码分别利用1～256不同核数运行，计算出加速比.缓冲和非缓冲模式下，并行的加速情况如图11所示.从图中可以看出，并行计算核心数增大到16个时，非缓冲模式加速比明显下降；而缓冲模式加速性优势明显，256核计算速度比单核提升约128倍，更适用于浅水方程的大规模并行计算.

本算例中所模拟的虚拟城市城区面积约为11.8 km2，与实际城市相比规模较小，例如目前天津市中心城区建成区面积约为281 km2，为本算例的23.8倍.为了论证实际大型城市中，利用并行计算进行洪水演进实时模拟的可行性，将数据规模进行扩展，推算所需计算时间如表2所示.

从表2可以看出，在使用256个计算核心大规模并行计算前提下，本算例仅需计算时间5 min，对一个城区面积100 km2的中小型城市，所需计算时间25 min，而对于面积400 km2的大型城市，则需70 min，与洪水的实际演进时间相当.考虑到本文采用简单的欧拉时间差分格式，且干湿判断容差较小，为避免数值发散，采用了dt=0.1 s的时间步长.如果通过进一步改进差分格式（如采用Runge-Kutta格式），并通过详细论证增大干湿判断容差，将时间步长增大10倍（dt=1 s），则所需计算时间可进一步缩短至7 min，能够实现大型城市洪水的实时仿真模拟，用于洪水发生后的快速决策和应急疏散.

5　结 论

（1）基于Riemann问题求解的Godnuov格式配合干湿判断动边界技术，能够很好地模拟溃坝洪水在建筑物密集城区的传播，再现溃坝水流水位壅高、水波反射、绕射和散射，以及低矮建筑的淹没过程等细节.

（2）建筑物在溃坝波波前到达初期且未被完全淹没前，所受水流荷载最大，包括静水压强和动水冲击（动压）荷载作用.

（3）建筑物的存在使得溃坝波在城区传播速度比平底情况减慢，而下游建筑物所受冲击荷载减小.

（4）缓冲模式数据交换比非缓冲模式更适用于浅水方程的大规模并行计算.

（5）基于目前的计算机硬件水平，使用256个计算核心能够对面积达400 km2的城区在70 min内完成洪水仿真模拟，进一步优化算法后能够将运算时间缩短至10 min以内，实现实时仿真模拟，用于洪水发生后的快速决策和应急疏散.

参考文献：

［1］ 白玉川，许 栋. 溃坝波在弯曲河道中传播的二维数值模拟［J］. 天津大学学报，2007，40（7）：771-778. Bai Yuchuan，Xu Dong. Two-dimensional numerical simulation of dam-break wave propagation in channel bends［J］. Journal of Tianjin University，2007，40（7）：771-778（in Chinese）.

［2］ 李大鸣，王 笑，赵明雨，等. 永定河泛区洪水调度数值模拟［J］. 天津大学学报：自然科学与工程技术版，2015，48（1）：76-86. Li Daming，Wang Xiao，Zhao Mingyu，et al. Flood dispatching numerical simulation for detention basins of Yongding river［J］. Journal of Tianjin University：Science and Technology，2015，48（1）：76-86（in Chinese）.

［3］ 安晨歌，傅旭东，马宏博. 几种溃坝模型在溃决洪水模拟中的适用性比较［J］. 水利学报，2012，43（2）：68-73. An Chenge，Fu Xudong，Ma Hongbo. Applicability of simulation models for dam-break flood due to overtopping［J］. Journal of Hydraulic Engineering，2012，43（2）：68-73（in Chinese）.

［4］ 王晓玲，张爱丽，陈华鸿，等. 三维溃坝洪水在复杂淹没区域演进的数值模拟［J］. 水利学报，2012，43（9）：1025-1033. Wang Xiaoling，Zhang Aili，Chen Huahong，et al. Three-dimensional numerical simulation of dam-break flood routingin the complex inundation areas［J］. Journal of Hydraulic Engineering，2012，43（9）：1025-1033 （in Chinese）.

［5］ 张大伟，程晓陶，黄金池. 建筑物密集城区溃堤水流二维数值模拟［J］. 水利学报，2010，41（3）：272-277. Zhang Dawei，Cheng Xiaotao，Huang Jinchi. 2-D nu-merical modeling of levee-breach floods in dense urban areas［J］. Journal of Hydraulic Engineering，2010，41（3）：272-277（in Chinese）.

［6］ 严珍珍，张 怀，范湘涛，等. 日本Mw9.0大地震激发全球地震波传播特性的数值模拟研究与对比分析［J］. 中国科学：地球科学，2014，44（2）：259-270. Yan Zhenzhen，Zhang Huai，Fan XiangTao，et al. Comparative analysis of the characteristics of the global seismic wave propagation excited by the Mw9.0 Tohoku earthquake using numerical simulation［J］. Science China：Earth Science，2014，44（2）：259-270（in Chinese）.

［7］ Dottori F，Todini E. Testing a simple 2 D hydraulic model in an urban flood experiment［J］. Hydrological Processes，2013，27（9）：1301-20.

［8］ 江春波，安晓谧，张庆海. 二维浅水流动的有限元并行数值模拟［J］. 水利学报，2002，5（5）：65-68. Jiang Chunbo，An Xiaomi，Zhang Qinghai. 2-D shallow water flow simulation using parallel arithmetic for FEM［J］. Journal of Hydraulic Engineering，2002，5（5）：65-68（in Chinese）.

［9］ 李铁键，刘家宏，和 杨，等. 集群计算在数字流域模型中的应用［J］. 水科学进展，2006，17（6）：841-845. Li Tiejian，Liu Jiahong，He Yang，et al. Application of cluster computing in the digital watershed model［J］. Advance in Water Resources，2006，17（6）：841-845（in Chinese）.

［10］ 周 洋，张景新. 浅水方程的并行化求解［J］. 力学季刊，2013，34（4）：607-613. Zhou Yang，Zhang Jingxin. Parallel simulation of shallow water flow［J］. Chinese Quarterly of Mechanics，2013，34（4）：607-613（in Chinese）.

［11］ 潘存鸿，鲁海燕，郑 君，等. 二维溃坝波数值模型及其应用［J］. 水力发电学报，2010（4）：89-95. Pan Cunhong，Lu Haiyan，Zheng Jun，et al. Twodimensional numerical model of dam-break flow and its application［J］. Journal of Hydroelectric Engineering，2010（4）：89-95（in Chinese）.

［12］ 孙 健，陶建华. 潮流数值模拟中动边界处理方法研究［J］. 水动力学研究与进展：A 辑，2007，22（1）：44-52. Sun Jian，Tao Jianhua. The study on simulation of moving boundaryin numerical tidal flow model［J］. Journal of Hydrodynamics：Series A，2007，22（1）：44-52（in Chinese）.

［13］ Ji C，Munjiza A，Avital E，et al. Saltation of particles in turbulent channel flow［J］. Physical Review E，2014，89（5）：052202.

［14］ Xu D，Kaliviotis E，Munjiza A，et al. Large scale simulation of red blood cell aggregation in shear flows［J］. Journal of Biomechanics，2013，46（11）：1810-1817.

［15］ Liang D，Falconer R A，Lin B. Comparison between TVD-MacCormack and ADI-type solvers of the shallow water equations［J］. Advances in Water Resources，2006，29（12）：1833-1845.

［16］ Thacker W C. Some exact solutions to the nonlinear shallow-water wave equations［J］. Journal of Fluid Mechanics，1981，107：499-508.

［17］ Zhao L，Guo B，Li T，et al. A well-balanced explicit/semi-implicit finite element scheme for shallow water equations in drying-wetting areas［J］. International Journal for Numerical Methods in Fluids，2014，75（12）：815-834.

（责任编辑：樊素英）

Simulation of Flood Propagation in Cities Using Large Scale Parallel Computation of Shallow Water Equations

Xu Dong1 2，PAyet David3，Ji Chunning1，Xu Bin1，Bai Yuchuan1，Liu Hongbo1
（1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai Jiao Tong University，Shanghai 200240，China；3. School of Civil Engineering，Tianjin University，Tianjin 300072，China）

Abstract：Mathematical model was established for dam-break flow based on finite volume method. Godunov scheme was adopted to evaluate the flux of the Riemann problem. Spatial decomposition using blocks was used for large scale parallelization and computation acceleration. With these，fine simulation of the flood propagation in urban cities was realized. Numerical simulation results show that：buildings experience the peak load from flow at the initial stage of the arrival of the dam-break wave front；owing to the wave dissipation and shielding effect by the upstream buildings，the load decreases with the increase of the distance to the dam-break gate；the existence of buildings slows down the propagation of the flood. Parallel computation tests show that the buffered data mode is more suitable for large scale parallel computation of shallow water equations than the non-buffered mode. Large scale parallel computation with current technique can fulfil real-time simulation of flood propagation in urban areas as large as 400 km2，which can scientifically support the fast decision and emergency evacuation when riverside or coastal cities experience flood threats from dam-break or tsunamis.

Keywords：flood；shallow water equation；dam-break；parallel computation

中图分类号：TV122.9

文献标志码：A

文章编号：0493-2137（2016）04-0341-08

DOI:10.11784/tdxbz201410010

收稿日期：2014-10-09；修回日期：2014-12-17.

基金项目：国家自然科学基金创新研究群体资助项目（51321065）；国家自然科学基金资助项目（51379144，50979066，51009105）；天津市应用基础与前沿技术研究计划资助项目（12JCQNJC05600，12JCQNJC02600）；全国优秀博士学位论文作者专项基金资助项目（201453）.

作者简介：许 栋（1980— ），男，博士，副教授，xudong@tju.edu.cn.

通讯作者：及春宁，cnji@tju.edu.cn.