台阶式海堤结构参数对堤前波浪特性的影响研究

骆文广，张小飞，吴金骏，杨国录

（1. 广西大学土木建筑工程学院，南宁 530004；2. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）



台阶式海堤结构参数对堤前波浪特性的影响研究

骆文广1 2，张小飞1，吴金骏1，杨国录2

（1. 广西大学土木建筑工程学院，南宁 530004；2. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

摘要：采用数值分析与物理模型试验相结合的方法，探讨了台阶式海堤与波浪相互作用的基本规律以及海堤的坡度和台阶高度对堤前波浪特性的影响.研究结果表明：当海堤台阶高度一定时，海堤的坡度越缓，台阶的相对宽度越大时，因堤前波浪壅高增大会导致波浪的反射系数越大，此时波浪在海堤台阶溯上流下过程中消耗的波浪能就会越多，波浪爬高会越小；当海堤坡度一定时，海堤台阶高度越大，台阶的相对高度越大时，因堤前增多的反射波与入射波叠加剧烈而会导致波浪的反射系数越大，此时因为海堤台阶上残余的波浪减少而导致转化成的波浪势能越少，所以波浪爬高也会越小.

关键词：海堤坡度；台阶高度；波浪反射系数；波浪爬高

网络出版时间：2015-06-15. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20150615.1131.001.html.

海堤是为了防护沿海地域居民的生命财产安全所采用的主要建筑.海堤与海浪相互作用时，堤前的波浪特性会发生变化，所以堤前波浪特性是海堤设计需要考虑的重要因素.在长期的海堤建设实践中，发现台阶式海堤具有较好的消浪效果和良好的安全性，同时还能满足亲水性海岸休闲空间的规划需求.目前台阶式海堤在国内外已得较好应用，如我国浙江仁和的条块石塘和绍兴、海宁等地的台阶斜坡式海塘［1］；广西合浦县西沙海堤和南域海堤、防城区谭蓬海堤和牛食水海堤、东兴市榕树头海堤等［2］；日本也已建有许多台阶式海堤.

国内外学者对海浪与台阶式海堤的相互作用开展了大量的研究，取得了较丰富的研究成果.在国内，林大原［3］以波浪水槽试验研究了波浪在台阶式海堤上的变形和溯升行为；张传军［4］通过数值方法模拟了台阶式海堤在规则入射波条件下的消浪效果；程禹平［5］以规则波水槽试验对卷波台阶式防浪堤进行了试验研究，揭示台阶防浪堤的波压力与浮托力分布特征.在国外，Saville［6］对复坡带平台的海堤波浪爬高引入了波浪折减影响系数的计算方法，该方法被美国海岸防护手册（SPM）所采用；Soliman等［7］对亲水性复坡海堤的越浪量进行了数值模拟研究；Wang等［8］基于二维线性波理论，通过特征函数的展开，研究了波浪对带平台的复式海堤的作用问题.

虽然国内外许多学者对海浪与海堤的相互作用开展了大量的研究，但对台阶式海堤与海浪的相互作用及其堤前波浪特性的研究比较缺乏，所以本文通过数值模拟和物理试验相结合的方法，对不同结构尺寸的台阶式海堤的结构参数对堤前波浪特性的影响规律进行了研究，研究后的规律有助于台阶式海堤在工程上的设计以及应用.

1　数值模拟

1.1模型建立

本文以FLUENT软件为计算平台，利用FLUENT的前理软件gambit建立模型、划分网格.在FLUENT里建立数值波浪水槽，采用FLUENT软件中VOF模型、Segregated求解器、标准-κε模型、压力速度耦合的PIOS算法求解非定常状态下的紊流问题［9］.

本文数值模拟造波为推板式造波，其原理是强迫水槽中运动水质点做水平运动，起到模拟水质点的波动效果.让造波板做简谐运动，即

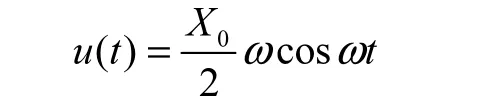
造出来的波的波面方程为

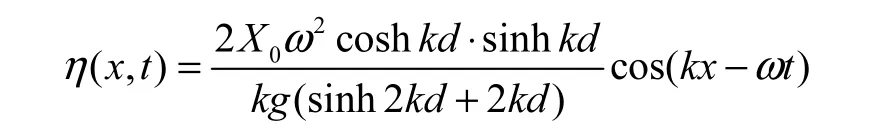
式中：X0为造波板冲程；k为波数，k=2π/L，L为波长；d为水深.在数值水槽的末端增加阻尼消波段，通过FLUENT中的UDF宏DEFINE_SOURCE编程实现消波.

在FLUENT软件中，使用二维非定常分离隐式求解器，选择多相流模型VOF，将相的数量设置为2，其中第一相设置为空气，第二相设置为水，自由面重构格式采用Geo-Reconstruct格式.湍流模式采用标准-κε湍流模型，近壁区流动采用标准的壁面函数法进行处理.在运行环境中设置参考压力值为101 325 Pa，并计及重力的影响，设置工作流体密度为1.225 kg/m3.

控制方程的离散项采用中心差分格式离散，对流项按如下格式离散：对于压力方程采用加权体积力（body force weighted）格式，对于动量方程、湍动能、湍动耗散率方程均采用二阶迎风格式.压力速度耦合方式采用PISO算法.将水槽正上方的边界设为压力入口边界条件，总压和静压均设为0.水池末端1倍波长范围内为阻尼消波段.左端为无滑移壁面边界，设为动边界，其余边界设为静止无滑移壁面边界.初始时刻，在自由面以上部分的计算区域中水的体积分数指定为0，混合物密度指定为1.225 kg/m3，在自由面以下部分的计算区域中，水的体积分数指定为1，混合物密度指定为998.2 kg/m3.湍流参数根据经验公式给定.取速度u=0 m/s作为流场的初始速度条件，由于采用动网格模型，因此取较小的时间步长，本算例取0.005 s，每步迭代20次.

图1为本文建立的二维波浪水槽，其模型尺寸为100 m×8 m，水深4 m，数值模型共有12万个单元格.

图1　波浪水槽模型示意Fig.1 Sketch of the wave flume model

图2　台阶式海堤数值模拟模型示意Fig.2 Sketch of stepped-seawall-structure under numerical analysis

1.2海堤结构对堤前波浪特性的影响研究

为了研究台阶式海堤的结构对堤前波浪特性的影响，本文在一个上边界长60 m、高8 m、水深4 m的数值波浪水槽右端分别建立了3种不同结构方案的台阶式海堤数值模型，模型整体示意如图2所示，5种方案的台阶式海堤结构尺寸如图3所示.采用推板式造波，造出4 m水深下，周期T=2.5 s，波长 L= 9.65 m，波高分别为0.2、0.3、0.4 m的试验工况，研究海堤结构对堤前波浪特性的影响.

图3　5种方案海堤结构尺寸（单位：cm）Fig.3 Five kinds of structure size charts of stepped-seawall-structure（unit：cm）

1.2.1海堤结构对波浪反射系数的影响

波浪在传播过程中遇到海堤后，将会有部分或者全部的波浪被反射回来，这部分反射回来的波浪与入射波产生波浪叠加而造成堤前波浪壅高，通常用反射系数KR来衡量海堤对波浪的反射程度［10］，且定义KR为反射波高HR与入射波波高H之比.在水槽波浪试验中，测定波浪反射系数的办法是，在水槽中沿着波浪传播方向上布置一组浪高仪，然后通过该组浪高仪测定波浪与海堤作用后合成波的最大波高Hmax和最小波高Hmin.文献［11］中提出了用波浪分离计算的Healy法来分别计算入射波波高H和反射波高HR，且定义H=（Hmax+Hmin）/2，HR=（Hmax-Hmin）/2.

由图3可知，方案1、2、3的海堤坡度m相同.在不同的规则波作用下，波浪反射系数KR会随着海堤的台阶高度h变化，其变化趋势如图4所示.而方案3、4、5的海堤台阶高度h是一定的.在不同的规则波作用下，波浪反射系数KR会随着海堤的坡度m变化，其变化趋势如图5所示.

图4　KR随海堤的台阶高度h的变化Fig.4 Change of KRwith the step height of the seawall

从图4可以看出：在同一入射波的工况下，KR随着海堤的台阶高度h的增加而增大，如在入射波波高0.2 m工况下，当h为10、20、30 cm时，KR分别是0.389、0.435、0.561.

图5　KR随海堤的坡度m的变化Fig.5 Change of KRwith the slope of the seawall

而由图5可知：在同一入射波的工况下，KR随着海堤坡度m的变缓而增大，如在入射波波高0.2 m工况下，m为1∶1.5、1∶2.0、1∶2.5时，KR分别是0.561、0.606、0.677.

1.2.2海堤结构对堤前波浪爬高的影响

为了研究台阶式海堤结构对波浪爬高的影响规律，引入折减影响系数来做评价指标［12］.定义无量纲参数KP为台阶式海堤的波浪爬高的折减影响系数，KP=RK/RP，其中RK为台阶式海堤的波浪爬高，RP为平面斜坡式海堤上波浪爬高.参数KP随着海堤的台阶高度h的变化趋势如图6所示，KP随着海堤坡度m的变化趋势如图7所示.

由图6可以看出：在同一入射波的工况下，KP随着海堤的台阶高度h的增加而减小，入射波波高0.4 m工况下，h为10、20、30 cm时，KP分别为0.463、0.422、0.380.

由图7可知：在同一入射波的工况下，KP随着海堤的坡度m的变缓而减小，在入射波波高0.4 m工况下，m为1∶1.5、1∶2.0、1∶2.5时，KR分别是0.380、0.371、0.356.

图6　KP随海堤的台阶高度h的变化Fig.6 Change of KPwith the step height of the seawall

图7　KP随海堤的坡度m的变化Fig.7 Change of KPwith the slope of the seawall

2　物理模拟

由于波浪的数值模型在模拟中引入了假定，使得计算结果近似度很大.为验证数值模型的规律，且深入研究堤前波浪特性，有必要通过物理模型试验来研究台阶式海堤结构参数对堤前波浪特性的影响规律.物理模型试验是在二维波流水槽中进行的，水槽长30.0 m、宽1.5 m、高1.5 m，水深1.0 m.

2.1试验设计

根据前人的试验经验［13］，本模型试验按重力相似准则设计模型，模型几何比尺为1∶10，根据试验正交性原则，从台阶式海堤的高度与坡度2个方面设计了5种结构方案的台阶式海堤，各种方案的模型如图8所示，海堤结构参数如表1所示.依据我国沿海地区波浪的实测资料设计了6组波浪入射工况，其波浪参数如表2所示，按照《波浪模型试验规程》［14］要求，每个试验模型在不同波浪类型下重复3次试验以上.在试验中测试并计算了波浪反射系数和波浪爬高2个方面的堤前波浪特性.选择从台阶式海堤结构与堤前波浪反射系数和波浪爬高之间的关系着手，分析海堤结构对堤前波浪特性的影响规律.

图8　各种方案海堤试验模型的结构尺寸Fig.8 Structure size for each seawall model scheme

表1　各模型方案的设计尺寸参数Tab.1 Design size parameters for each model scheme

表2　台阶式海堤试验的波浪参数Tab.2 Wave parameters for stepped seawall wave dissipation tests

2.2海堤结构对堤前波浪特性的影响试验

海堤的坡度及其台阶高度是制约海堤堤前波浪特性的2个重要因素［2］.为了研究海堤坡度对堤前波浪特性的影响，基于变量控制法的原理，选取海堤台阶高度为0.03 m、3种海堤坡度（1∶2、1∶3、1∶4）方案进行试验.同时，为了研究海堤台阶高度对堤前波浪特性的影响规律，以海堤坡度1∶2的台阶式海堤为研究对象，增加了两组台阶高度（0.02、0.04 m）试验，与前面的台阶高度0.03 m的试验进行对比.

为了清晰客观地分析台阶式海堤的结构对波浪特性的影响规律，将海堤台阶的宽度B和台阶的高度D进行无量纲化（B/Hs、D/Hs），其中Hs为入射波的试验有效波高.由于试验时水槽中水深一定，当海堤坡度相同时，那么从静水面起算，到海堤坡脚处的海堤总宽度ΣB是一定的.当试验有效波高Hs一定时，海堤的相对总宽度ΣB/Hs是一定的；此时各种方案的台阶高度D不同，从静水面起算的台阶总高度ΣD也不同，在同一试验有效入射波高Hs作用下，海堤的相对总高度ΣD/Hs是不同的.因此，只需分析海堤的相对总高度ΣD/Hs对堤前波浪特性的影响规律即可.同理，当海堤的台阶高度一定时，海堤台阶的相对总高度ΣD/Hs一定，所以只分析海堤的相对总宽度ΣD/Hs对堤前波浪特性的影响规律即可.

2.2.1海堤结构对堤前波高影响的试验

波浪与台阶式海堤作用时，在波浪与台阶相互作用过程中，通过撞击、爬升、破碎、漩滚等会大量消耗入射波的能量，但通常情况下，入射波的能量不可能完全耗尽，因此，入射波作用在台阶海堤上时会发生反射，反射回去的波浪与入射波相互作用后，造成堤前波浪波高发生变化，出现壅高，壅高的高度越小，说明反射的能量越小，波浪与台阶相互作用时消耗的能量越大，所以可分析波浪反射系数KR的变化来研究堤前波高的变化.图9为KR随海堤的相对总宽度ΣD/Hs的变化情况，图10为KR随海堤的相对总高度ΣD/Hs的变化情况.

由图9可知：在同一入射波作用下，当ΣD/Hs越大时，波浪的反射系数KR越大.即在同一入射波作用下，当海堤的台阶高度相同时，海堤的坡度越缓，海堤台阶的宽度越大，海堤上的波数越多，反射波与入射波叠加越剧烈，所以堤前波浪的反射系数就越大.当海堤的相对总宽度为1.60、2.40、3.20时，在入射规则波波高1.5 m工况下，KR分别为0.898、1.050、1.148；在入射不规则波波高1.5 m工况下，KR分别为0.308、0.501、0.636.

图9　KR随海堤相对总宽度ΣB/Hs的变化Fig.9 Change of KRwith the relative total width ΣB/Hs

由图10可知：在同一入射波作用下，当ΣD/Hs越大时，波浪的反射系数KR越大.即在同一入射波作用下，海堤的台阶高度越大，海堤反射的波浪增多，反射波波能加大，所以海堤堤前波浪的反射系数就越大.当海堤相对总高度为6.90、9.18、14.40时，在入射规则波波高1.0 m工况下，KR分别为1.000、1.085、1.260；在入射不规则波波高1.0 m工况下，KR分别为0.309、0.360、0.444.

2.2.2海堤结构对波浪爬高影响的试验

根据试验中测得的波浪爬高分布曲线，可以求得海堤堤面台阶上的波浪爬高RK［15］.由于单坡海堤的波浪爬高计算公式在《海港水文规范》、《堤防技术工程规范》［16］中都有相应的说明，所以可以分别计算出各种工况下，不同海堤坡度的平面斜坡式海堤的波浪爬高RP.因此可得出海堤的相对总高度ΣD/Hs和相对总宽度ΣD/Hs对波浪爬高的折减影响系数KP的影响规律.图11所示为KP随ΣD/Hs的变化，图12所示为KP随ΣD/Hs的变化.

由图11可知：在台阶相对高度一定时，当海堤的ΣD/Hs越大，KP越大.即在同一入射波作用下，当海堤的台阶高度相同时，海堤台阶的宽度越大，波浪在平台上破碎损耗的紊动波浪能就越大，波浪在海堤台阶的爬高越小，所以KP将越大.在入射规则波波高2.5 m工况下，海堤的相对总宽度为0.96、1.44、1.92时，KP分别是0.56、0.60、0.61；在入射不规则波波高1.5 m工况下，海堤的相对总宽度为1.60、2.40、3.20时，KP分别为0.65、0.70、0.71.

图11　KP随海堤的相对总宽度ΣB/Hs变化Fig.11 Change of KPwith ΣB/Hs

图12　KP随海堤的相对总高度ΣB/Hs变化Fig.12 Change of KPwith ΣB/Hs

由图12可知：当海堤相对宽度一定时，当海堤的ΣD/Hs越大，KP越大.即在同一入射波作用下，当海堤的台阶宽度相同时，海堤台阶的高度越大，波浪与台阶竖直面作用后被反射的程度就越剧烈，因此波浪在海堤台阶上残余波浪的波能势必越小，所以KP越大.在入射规则波波高2.0 m工况下，海堤相对总高度3.45、4.70、7.20时，KP分别是0.55、0.58、0.62；在入射不规则波波高1.0 m工况下，海堤的相对总高度为6.90、9.18、14.40，KP分别是0.59、0.63、0.70.

3　结 论

（1）当台阶式海堤的台阶高度一定时，随着海堤的坡度变缓，海堤的台阶宽度增大，在同一入射波作用下有：

①海堤上的波数增多，反射波与入射波叠加加剧，因此海堤堤前波浪的反射系数会随着海堤相对宽度的增大而增大，即海堤堤前波浪的反射程度会随着海堤坡度的变缓而加剧；

②入射波浪在海堤台阶的平台上破碎紊乱而消耗的波浪能会增多，波浪在海堤堤面的台阶上的爬升势能减小，因此波浪爬高的折减影响系数就会随着海堤相对宽度的增大而减小，即波浪爬高会随着海堤坡度变缓而减小.

（2）当台阶式海堤的海堤坡度一定时，随着台阶高度的增大，海堤的台阶宽度增大，在同一入射波作用下有：

①海堤反射的波浪增多，反射波波能加大，海堤堤前的波浪的反射系数增大；

②入射波浪在海堤台阶的平台上残余的波浪减少，海堤上的波浪波能减弱，波浪在堤面的台阶上转化的爬升势能会减小，因此波浪爬高的折减影响系数就会随着海堤相对高度的增大而减小，即波浪爬高会随着海堤台阶高度增大而减小.

参考文献：

［1］ 毛昶熙，段祥宝，毛佩郁. 东南沿海海堤现状调研报告［J］. 海洋工程，1996，14（2）：28-39. Mao Changxi，Duan Xiangbao，Mao Peiyu. An investigation report on south-east coastal levees ［J］. The Ocean Engineering，1996，14（2）：28-39（in Chinese）.

［2］ 骆文广. 台阶式海堤堤前波浪特性试验研究［D］. 南宁：广西大学土木建筑工程学院，2014. Luo Wenguang. Study on the Wave Characteristics Before the Stepped-Seawall ［D］. Nanning：College of Civil Engineering and Architecture，Guangxi University，2014（in Chinese）.

［3］ 林大原. 阶梯式海堤上波浪特性之研究［D］. 台湾：国立成功大学工学院，1992. Lin Dayuan. Study on the Wave Characteristics on the Stepped-Seawall ［D］. Taiwan：College of Engineering，National Cheng Kung University，1992 （in Chinese）.

［4］ 张传军. 阶梯式海堤消浪效果研究［D］. 南宁：广西大学土木建筑工程学院，2013. Zhang Chuanjun. Study on Wave-Damping Effectiveness of the Stepped-Seawall ［D］. Nanning：College of Civil Engineering and Architecture，Guangxi University，2013（in Chinese）.

［5］ 程禹平. 新型卷波弧形台阶防浪堤［J］. 人民珠江，1995（4）：35-38. Cheng Yuping. A new kind of step type curved breakwater ［J］. Pearl River，1995（4）：35-38（in Chinese）.

［6］ Saville T Jr. Wave run-up on composite slopes ［J］. Coastal Engineering Proceedings，1957，1（6）：41-49.

［7］ Soliman A，Reeve D. Numerical study for small negative freeboard wave overtopping and overflow of sloping sea wall，coastal structures 2003［C］// Proceedings of the Conference on Coastal Structures 2003. Oregon，USA，2003：643-655.

［8］ Wang K-H，Shen Q. Wave motion over a group of submerged horizontal plates ［J］. International Journal of Engineering Science，1999，37（6）：703-715.

［9］ 许松林，赵 婵. 气液并流垂直液膜流动的数值模拟［J］. 天津大学学报：自然科学与工程技术版，2014，47（12）：1039-1046. Xu Songlin，Zhao Chan. Numerical simulation of cocurrent gas-liquid vertical liquid film flow ［J］. Journal of Tianjin University：Science and Technology，2014，47（12）：1039-1046（in Chinese）.

［10］ Frigaard P，Brorse M. A time-domain method for separating incident and reflected irregular waves ［J］. Coastal Engineering，1995，24：205-215.

［11］ Heins A E. Water waves over a channel of finite depth with a submerged plane barrier ［J］. Canadian J Math， 1950（2）：210-222.

［12］ de Waal J P，van der Meer J W. Wave run-up and overtopping on coastal structures［C］//Proceedings of Coastal Engineering Conference. Venice，Italy，1992，23：1758-1771.

［13］ 陈汉宝，刘海源，徐亚男，等. 风浪与涌浪相互影响的实验［J］. 天津大学学报：自然科学与工程技术版，2013，46（12）：1122-1126. Chen Hanbao，Liu Haiyuan，Xu Yanan，et al. Experiment on interaction between wind wave and swell ［J］. Journal of Tianjin University：Science and Technology，2013，46（12）：1122-1126（in Chinese）.

［14］ 中国人民共和国交通部. 波浪模型试验规程［M］. 北京：人民交通出版社，2002. Ministry of Transport of the People’s Republic of China. Regulation of Wave Model Experiments ［M］. Beijing：China Communication Press，2002（in Chinese）.

［15］ Chen Guoping，Yu Kuangming，Zhang Jiachang. Effect of berm width and elevation on irregular wave run-up ［J］. China Ocean Engineering，1991，5（4）：441-452.

［16］ 中国人民共和国交通部. JTS 145—2—2013 海港水文规范［S］. 北京：人民交通出版社，2013. Ministry of Transport of the People’s Republic of China. JTS 145—2—2013 Code of Hydrology for Sea Harbour ［S］. Beijing：China Communication Press，2013（in Chinese）.

（责任编辑：赵艳静）

Influence of Stepped-Seawall-Structure Parameters on the Characteristic of Wave in Front of Seawall

Luo Wenguang1 2，Zhang Xiaofei1，Wu Jinjun1，Yang Guolu2
（1. Civil and Architecture Engineering College，Guangxi University，Nanning 530004，China；2.State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China）

Abstract：To study the influence of stepped-seawall-structure parameters on the characteristic of wave in front of seawall，a method combined numerical analysis with physical model test was chosen to research the basic rule of interaction between stepped-seawall structure and wave，still learn the influence of seawall slope and the height of the step to the characteristic of wave in front of seawall at the same time.The result shows that if the height of seawall step is fixed，the seawall slope is slower，the relative width of the steps is greater，meanwhile，for the reason that the increase of the rise of wave before seawall could lead greater wave reflection coefficient，in this case，the wave energy dissipation could be more in the process of climbing and defluxion on seawall steps；if the seawall slope is fixed，the height of the seawall step is higher，the relative height of the step is greater，due to the severe superposition of increasing reflection wave and incident wave could lead greater reflection coefficient of waves，based upon this point，because the decrease of the residual waves on the seawall step lead less potential energy of wave，so the wave run-up could be smaller.

Keywords：seawall slope；height of the steps；wave reflection coefficient；wave run-up

中图分类号：TV39

文献标志码：A

文章编号：0493-2137（2016）04-0408-07

DOI:10.11784/tdxbz201503075

收稿日期：2015-03-25；修回日期：2015-05-25.

基金项目：国家自然科学基金资助项目（51109167）.

作者简介：骆文广（1988— ），男，博士研究生，Luowengg@126.com.

通讯作者：张小飞，gxxfzhang@sina.com.cn.