小清河滞洪区洪水演进数学模型的研究

李大鸣，范 玉 2，杨紫佩，李杨杨

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 华北水利水电大学水利学院，郑州 450011）



小清河滞洪区洪水演进数学模型的研究

李大鸣1，范 玉1 2，杨紫佩1，李杨杨1

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 华北水利水电大学水利学院，郑州 450011）

摘要：随着我国经济的发展，蓄滞洪区的开发和建设越来越受到人们的关注，对滞洪区进行洪水演进数值模拟研究非常必要.本文采用有限体积法建立了二维洪水演进数学模型，并对洪水演进的水量平衡计算模式进行改进，提出单元水量出流修正法，消除了有限体积法单元体内出现负水深，产生虚假流动的现象.将该研究成果应用于小清河滞洪区洪水演进的数值模拟，采用实测资料，对小清河滞洪区50年一遇洪水演进进行验证和模拟，从而得到泛区内洪水形势及淹没情况，为滞洪区分洪调度提供理论指导.

关键词：小清河滞洪区；洪水演进；水量平衡；有限体积法

网络出版时间：2015-09-01. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20150901.0944.008.html.

洪水波在行进过程中，水位、流量、速度等运动要素随时间发生剧烈的变化，属于非恒定流的研究范畴，多年来研究人员对其进行了大量的研究.法国学者圣·维南在1871年首先提出了描述一维非恒定流的基本方程——圣维南方程组［1］，为非恒定水流运动提供了理论依据，但由于方程是拟线性的双曲型偏微分方程组，在数学上难以求解其精确的理论解，实际应用中常将方程组进行简化.随着计算机水平的逐步提高，研究者们开始利用计算机对圣维南方程组进行数值求解，并建立了大量的水动力数学模型，模型计算精度和模拟结果取得了很大的提高［2］.模型的构建过程主要包括控制方程的离散及求解，用数值解近似代替解析解.目前离散的主要方法包括有限元法、特征线法、有限差分法、有限体积法和有限分析法等，许多学者已经对此进行了大量研究［3-7］.

1991年，刘树坤等［8］利用结构网格对小清河分洪区洪水演进进行了数值模拟；Elliot等［9］运用特征理论，计算了弯道中的洪水波演进；Glaister［10］在一维计算的基础上，将通量差分分裂技术与通量限制函数相结合的近似黎曼解法推广到二维问题；1995年，王船海等［11］为解决无资料地区径流如何流入干流以及如何将河网一维水流模拟与行蓄洪区二维水流模拟耦合统一求解的问题，建立了行蓄洪区型流域洪水模型；谭维炎等［12］应用二维有限体积法、Osher格式及间断拟合法进行了钱塘江口涌潮的数值模拟，其中对涌潮作了局部一维处理；1998年，李大鸣等［13］对Galerkin有限元质量集中法进行了改进，提出了质量加权集中法；谢作涛等［14］从求解一维对流方程的Holly-Preissmann格式出发，结合有限差分法建立了一维洪水演进数学模型，并将该模型应用于长江荆江河段洪水演进计算，模拟的洪水传播过程基本与实际吻合；付典龙等［15］以圣维南方程组为基本方程，利用特征线法建立了一维数学模型，并将该模型应用于赣江支流锦江的模拟计算中；李大鸣等［16］在2009年采用有限体积法建立了适应河道、滞洪区复杂情况的一二维衔接洪水演进数学模型，该模型考虑了窄、宽河道以及洼淀等不同情况的嵌套和衔接，随后又在对永定河泛区的洪水演进数值模拟中，提出了具有旁侧出流的河网独立计算的一、二维多口门嵌套衔接模式，建立了一维河道与平面二维衔接的洪水演进数学模型.

应用有限体积法进行洪水演进计算时由于计算模式本身的不足，常常会引起某些单元体出现水量不平衡的现象，在单元体内会出现负水深的现象，产生虚假流动，这种现象对模型整体水流趋势不会造成很大的影响，却会引起模型总水量的偏差.为此，本文通过对水量平衡算法进行改进，对小清河滞洪区的洪水演进进行了数值模拟.

1　基本控制方程

有限体积法在不规则网格上适应性较好，计算精度较高，能够满足因变量的积分在任意一组控制体积内均守恒的特点，能很好地适应本模型的研究要求，因此本文选用有限体积法进行方程的离散.

1.1二维非恒定流基本方程

连续方程

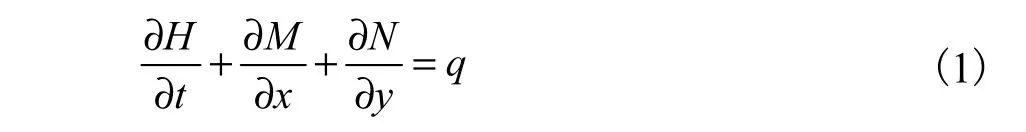
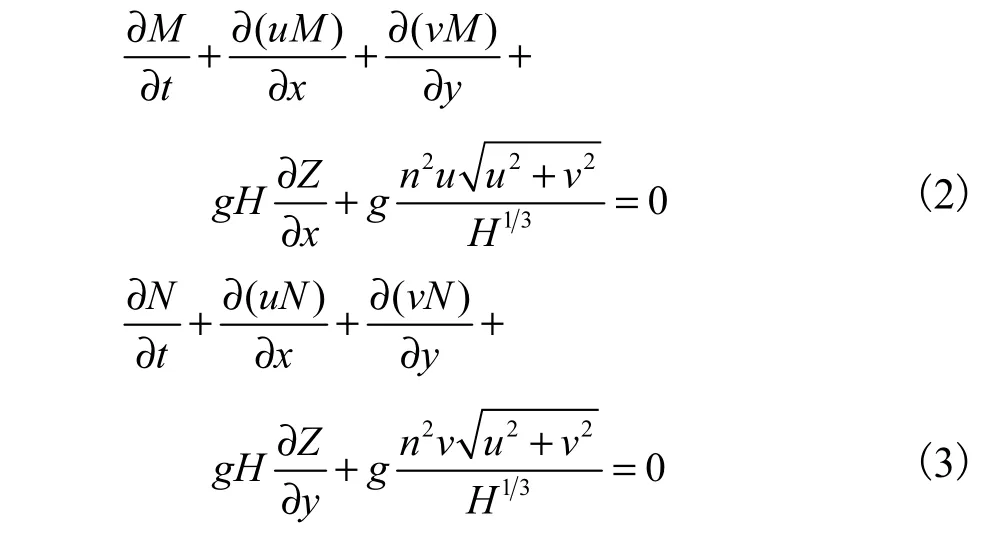
式中：H为水深；M、N分别为x、y方向上的单宽流量，且M= Hu，N= Hv；u、v分别为流速在x、y方向上的分量；q为源汇项；Z为水位，Z= Z0+ H，Z0为底高程；n为糙率；g为重力加速度.

1.2方程的离散

1.2.1连续方程的离散

1.2.2运动方程的离散

由于滞洪区实际地形较为复杂，对运动方程进行离散时可将滞洪区内复杂的地形按照地面型通道、河道型通道和缺口堤或连续堤通道进行模块化处理.

（1）地面型通道.即通道两侧网格单元均为比较平坦的陆地地面，同时该通道上没有堤防等阻水建筑物.此种情况下滞洪区内地形起伏变化较小，可省略方程中的加速度项，而保留起主要作用的重力项和阻力项，利用差分法离散式（2）～（3），从而得到离散的动量方程为

（2）河道型通道.即通道两侧网格单元均为河道型网格单元，此时受河道地形影响，同时考虑方程中的重力项、阻力项和加速度项，通过差分法可得到其离散方程为

（3）连续堤或缺口堤通道.公路、铁路、连续堤防等高于地面的阻水建筑物，其流量采用宽顶堰溢流公式计算，离散后可化为

式中：m为宽顶堰流流量系数；sσ为淹没系数.

（4）过水建筑物的处理.跨越阻水边界的过水建筑物，如公路桥涵、涵洞等，起连接上下游水流的作用.计算区域内的桥、涵洞等无压水流按式（7）进行计算.

（5）特殊单元处理.有压隧洞水流计算式为

式中：ω为有压隧洞断面面积；φ为有压隧洞出流流量系数，取0.65～0.70；Δzj为通道上下游单元水头差；Bj为第j个通道的长度.

2　水量平衡算法的改进

应用有限体积法进行模型计算的优点在于将方程进行离散时能够保证在任一组控制体内均守恒，但由于计算模式自身的缺点，常常会引起某些单元体出现水量不平衡的现象，即出现单元体入流量与出流量不相等的情况.换而言之，在单元体内会出现负水深的现象，产生虚假流动，这种现象对模型整体水流趋势不会造成很大的影响，却会引起模型总水量的偏差，因此，本文通过下面的方法对模型进行改进和提高.本模型应用无结构不规则网格进行模型前期处理，整个模型网格包括三角形、四边形和五边形，以图1为例进行说明，其中单元O为中心网格，与A、B、C、D 4个网格毗邻，整个计算模式以T、T+dt和T+2dt 3个时间步长节点为1个单位时间计算过程（依照方程离散时的格式进行选取），整个时间范围内依次重复此单位时间内的处理过程.假定T时刻单元O、A、B、C、D内水深分别为H、HA、HB、HC、HD.

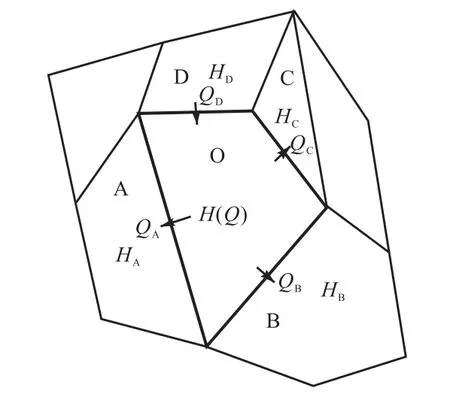
图1　计算网格示意Fig.1 Computing grids diagram

1）未改进前的计算模式

本模型计算时采用时间步长跳跃和空间步长交错格式分别计算过流通道的流量和单元格内的水位，以图1进行说明，此处仅选用地面型通道为例进行介绍.假定T时刻时各单元格内水位均已知，则利用式（5）计算得出T+dt时刻通过各个通道的流量QA、QB、QC、QD，再由连续性方程（4）求得T+2dt时刻单元格O的水深HT+2d t，若计算求得其水深HT+2d t为负，则直接将水深赋值为0（在整个模型计算中出现负水深是不合理的），此为一个计算水深和流量的过程，在整个时间内依次循环这一过程完成整个计算.

2）改进的计算模式

用模式1）计算时，当单元格内出现负水深时，将其赋值为零将会增加水量，从而导致不平衡现象，引起虚假流动.对此模式进行改进，主要分3个阶段.

（1）当利用式（4）计算T+2dt时刻单元O内水深为负时（假定此时出现的负水深为-h），对计算模式进行修正，重新计算T+dt时刻的出流，根据所得的负水深-h分别将出流QA、QB、QC按比例缩减，重新得到此时的出流QA1、QB1、QC1，保证单元格O不出现负水深.

（2）上一阶段中只对出流进行修正而未对来流进行处理，在T+dt时间层面上对不同单元格的出流进行修正的同时相当于对其相邻的单元的入流也进行了修正，假定此时修正后的入流为 QD1，按照此时单元O向A、B、C单元泄流的比例重新分配，则出流值修正值分别为 QA2、QB2、QC2，对流量进行修正时保证QA2≤QA、QB2≤QB、QC2≤QC.

（3）应用步骤（2）中得到的出流对单元O的入流重新进行修正，将入流量按比例重新分配给此时单元O的出流，保证其出流量不大于连续方程的计算值.

3　洪水演进数值模拟

3.1工程范围与网格划分

小清河蓄滞洪区位于大清河系北支中上游大宁水库以下，区域范围跨越北京市和河北省，东临永定河右堤及高地，西侧接山区前高地，向南延展至古城小埝和小营横堤.滞洪区流域规划如图2所示.

根据小清河行洪区的地形和河道横纵断面的资料以及北拒马河三支河道带状地形图采集的地形数据，采用非结构网格自动生成技术进行网格的剖分，以正方形网格为主，局部辅以三角形、五边形、六边形网格，最终形成整个模型范围内的无结构网格.通过以上网格划分和处理，模型范围内设置了25 471个结点、24 385个单元、49 863个通道，见图3.

图2　小清河滞洪区流域规划Fig.2 Watershed planning of Xiaoqing River detention area

图3　小清河模型网格剖分Fig.3 Grid subdivision of Xiaoqing River model

3.2模型验证

3.2.1入流条件

模型的上边界条件，主要指向小清河分洪区内进行分流的河流洪水过程.主要入流地点在张坊村附近，入流洪水总量以白沟河东茨村站为总控制，以1990年12月编制的《大清河流域设计洪水分析报告》成果为依据，包括北拒马河、大石河、胡良河、小清河、刺猬河和哑巴河等河流来水.东茨村站设计洪水过程为：张坊与东茨村采用同频率洪水，其他河流采用相应频率洪水进行组合.图4为50年一遇不同河流的来流过程.

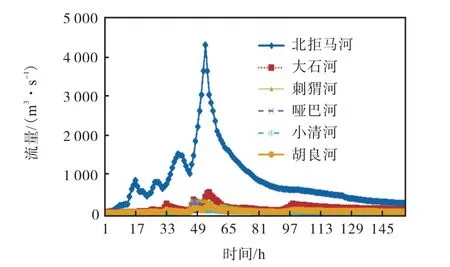
图4　50年一遇不同河流的来流过程Fig.4 Flood inflow process of 50-year return period

3.2.2出流边界条件

遇设计标准及其以下洪水时，小清河分洪区的洪水出口为白沟河；遇超标准洪水时，除利用白沟河进行分洪外需同时利用小营横堤扒口向兰沟洼分洪，此时白沟河东茨村断面的水位泄量关系和小营横堤分洪口门均作为模型的下游边界.白沟河东茨村断面水位流量关系见表1.

表1　白沟河东茨村断面水位流量关系Tab.1 Relationship between water level and discharge of Dongci Village of Baigou River

3.2.3水位验证

根据现有资料对50年一遇洪水的最高水位分别选3组数据点（通过横、纵坐标确定该点）的方法选取12个点进行验证，验证点在模型范围内的位置见图5. 验证点设计水位与模拟水位的对比结果见表2.

图5　模型水位验证点Fig.5 Verification point of water level in the model

由表2可知，模拟小清河滞洪区50一遇洪水演进过程所得到的模拟水位与设计水位相比较，最大误差为0.253 m，出现在涿州市西部北拒马河中支和北拒马河交汇处；误差大于0.200 m的另一位置在京广铁路与北拒马河交汇处；其他计算误差均小于0.160 m，误差主要原因是模型较难重复确定设计水位时的地形、地貌和糙率系数等条件.但模型计算流动趋势合理，洪水位误差不大，说明模型可用于工程模拟计算.

表2　50年一遇洪水水位比较Tab.2 Comparison of water level of 50-year return period

3.3数值模拟

3.3.1洪水演进模拟

小清河蓄滞洪区及涿州市城市防洪标准为50年一遇，本文对50年一遇洪水对涿州城区安全的影响程度进行了数值模拟，见图6和图7.

图6　50年一遇洪水演进过程（18、39、60、81 h）Fig.6 Flood routing process of 50-year return period （18、39、60、81 h）

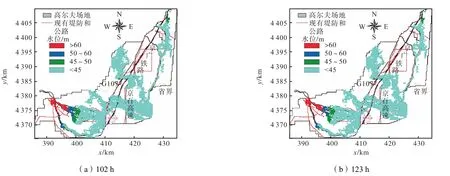
图7　50年一遇洪水演进过程（102、123 h）Fig.7 Flood routing process of 50-year return period （102、123 h）

3.3.2洪水淹没分析

图8为50年一遇最大水深，通过计算可得50年一遇时小清河分洪区动态高水位下的淹没面积为356 km2，蓄水容积为5.4亿m3.在蓄水淹没面积中，深水区（蓄洪水深3.0 m以上）面积占涿州总淹没面积的9.9% ，中等深水区（蓄洪水深0.5～3.0 m）面积占涿州总淹没面积的47.9% ，浅水区（蓄洪水深0.5 m以下）面积占涿州总淹没面积的42.2% .不同蓄洪水深情况见表3.

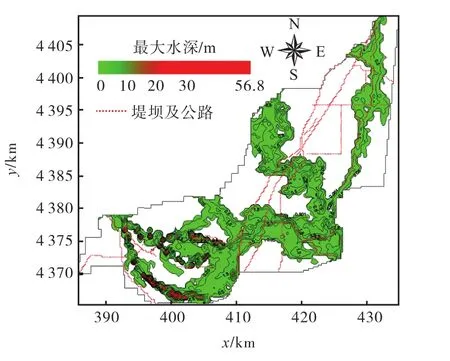
图8　50年一遇最大水深Fig.8 Maximum water depth of 50-year return period

表3　涿州市不同蓄洪水深情况统计Tab.3 Statistics of different storage water depths in Zhuozhou city

3.4算法改进成果

将修正后的计算模式得到的50年一遇洪水计算结果与修正前计算结果进行对比分析，不同计算时段的对比结果见表4.

由表4可以看出模式修正前第1 h时来流量与计算所得的总水量无明显差别，随着计算时间的增长，来流量与计算总水量逐步出现较大的偏差，至计算到124 h时计算总水量比来流量多出约2.27亿m3，与前面提出的因将负水深强制为零带来虚假流动的理论相吻合；而将模式进行改进后，可以看出自初始时刻至模型计算时间结束，整个模型的来流量与计算总水量基本是相等的，说明修正模型后在水量计算精度上得到大幅度的提高，具有一定的参考价值.

表4　改进前后计算结果比较Tab.4 Comparison of computational results before and after improvement

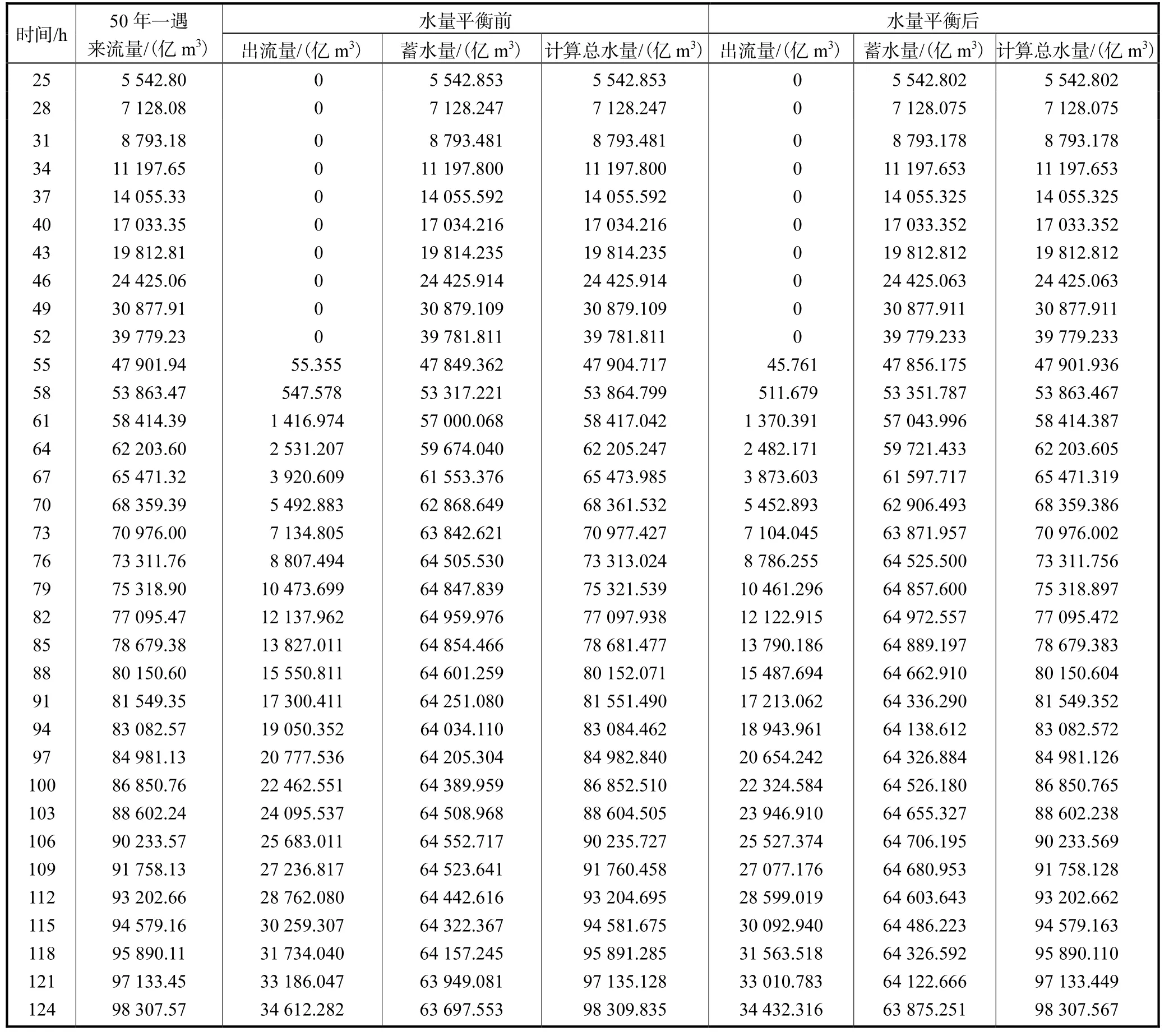
续表4

4　结 语

本文通过对有限体积法水量平衡算法进行改进，在一定程度上避免了单元体内负水深和虚假流动现象，提高了模型水量平衡计算的精度.采用无结构不规则网格的处理方式，对小清河滞洪区50年一遇最大水深进行验证，验证结果表明该模型建立基本合理，对小清河滞洪区洪水演进数值模拟的结果具有一定的应用价值.

参考文献：

［1］ Mccarthy G T. The Unit Hydrograph and Flood Routing ［R］. Presented at Conf North Atl Div US Crops Eng，1938.

［2］ 徐卫红. 洞庭湖区复杂防洪系统数值模拟模型研究与应用［D］. 北京：中国水利水电科学研究院，2013. Xu Weihong. Research and Application of Complicated Flood Control System Mathematical Model in Dongting Lake Area ［D］. Beijing：China Institute of Water Resources and Hydropower Research，2013（in Chinese）.

［3］ 熾胡祖. 数值流体动力学［J］. 力学进展，1973（5）：75-98. Hu Zuchi. Numerical methods in fluid dynamics ［J］. Advances in Mechanics，1973（5）：75-98（in Chinese）.

［4］ 纽 曼，威瑟斯庞. 用有限单元法解有自由面的不稳定流［J］. 水利水运科技情报，1975（S1）：39-54. Neuman S P，Witherspoon P A. Analysis of unsteady flow with a free surface using the finite element method ［J］. Water Conservancy and Water Transportation Sci-ence and Technology Information，1975（S1）：39-54（in Chinese）.

［5］ 刘德有，索丽生. 复杂给水管网恒定流计算新方法——特征线法［J］. 中国给水排水，1994，10（3）：19-24，3. Liu Deyou，Suo Lisheng. A new method for steady flow in pipe network—Characteristic method ［J］. China Water & Wastewater，1994，10（3）：19-24，3（in Chinese）.

［6］ 赵明登，郑邦民. 三维对流扩散方程的混合有限分析解［J］. 水利学报，1995（9）：55-62. Zhao Mingdeng，Zheng Bangmin. Mixing finite analytic method for 3-dimension convection-diffusion equations ［J］. Journal of Hydraulic Engineering，1995（9）：55-62（in Chinese）.

［7］ 谭维炎. 计算浅水动力学［M］. 北京：清华大学出版社，1998. Tan Weiyan. Calculation of Shallow Water Hydrodynamics ［M］. Beijing：Tsinghua University Press，1998（in Chinese）.

［8］ 刘树坤，李小佩，李士功，等. 小清河分洪区洪水演进的数值模拟［J］. 水科学进展，1991，2（3）：188-193. Liu Shukun，Li Xiaopei，Li Shigong，et al. Numerical simulation of flood routing in the Xiaoqinghe Flood Plain ［J］. Advances in Water Science，1991，2（3）：188-193（in Chinese）.

［9］ Elliot R C，Chaudhry M H. A wave propagation model for two-dimensional dam-break flows ［J］. J of Hydr Res，1992，30（4）：467-483.

［10］ Glaister P. Flux difference splitting for open channelflows ［J］. Int J of Number Meth Fluids，1993，16：629-654.

［11］ 王船海，李光炽. 行蓄洪区型流域洪水模拟［J］. 成都科技大学学报，1995（2）：6-14. Wang Chuanhai，Li Guangzhi. Flood modeling for basin with regions of flood storage and relief ［J］. Journal of Chengdu University of Science and Technology，1995（2）：6-14（in Chinese）.

［12］ 谭维炎，韩曾萃. 钱塘江口涌潮的二位数值模拟［J］.水科学进展，1995，6（2）：83-93. Tan Weiyan，Han Zengcui. Two-dimensional numerical simulation of estuary tidal bore of the Qiantang River ［J］. Advances in Water Science，1995，6（2）：83-93（in Chinese）.

［13］ 李大鸣，陈 虹，李世森. 河道洪水演进的二维水流数学模型［J］. 天津大学学报，1998，31（4）：439-445. Li Daming，Chen Hong，Li Shisen. A 2-D numerical model of propelling flood in the river ［J］. Journal of Tianjin University，1998，31（4）：439-445（in Chinese）.

［14］ 谢作涛，张小峰，谈广鸣，等. 一维洪水演进数学模型研究及应用［J］. 武汉大学学报：工学版，2005，38（1）：69-72. Xie Zuotao，Zhang Xiaofeng，Tan Guangming，et al. Study and application of mathematical model for onedimensional flood-routing ［J］. Engineering Journal of Wuhan University，2005，38（1）：69-72（in Chinese）.

［15］ 付典龙，傅 春. 一维圣维南方程组的特征线法［J］.南昌大学学报：工学版，2006，28（4）：386-389. Fu Dianlong，Fu Chun. The eigenfunction method of one-dimensional Saint-Venant equations ［J］. Journal of Nanchang University：Engineering & Technology，2006，28（4）：386-389（in Chinese）.

［16］ 李大鸣，林 毅，徐亚男，等. 河道、滞洪区洪水演进数学模型［J］. 天津大学学报，2009，42（1）：47-55. Li Daming，Lin Yi，Xu Yanan，et al. Numerical model of flood propagation of rivers and flood detention basin ［J］. Journal of Tianjin University，2009，42（1）：47-55（in Chinese）.

（责任编辑：赵艳静）

Flood Routing Numerical Model of Xiaoqing River Detention Area

Li Daming1，Fan Yu1 2，Yang Zipei1，Li Yangyang1
（1.State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China：2.School of Water Conservancy，North China University of Water Resources and Electric Power，Zhengzhou 450011，China）

Abstract：With the civil economic development the use of flood detention area has drawn more and more attention from people，so it is very necessary to carry out the flood routing numerical simulation study on the flood detention area.A 2D flood routing numerical model was established with finite volume method（FVM） and a correction method for a unit of water flow was proposed to improve the water balance computing model，which eliminates the negative depth and false flow phenomenon in finite volume method.The improved approach was used to numerically simulate Xiaoqing River detention area.The flood routing of 50-year return period was tested and simulated with measured data，and water level and submerged scope were obtained，which provides theoretical guidance for flood diversion.

Keywords：Xiaoqing River detention area；flood routing；water balance；finite volume method

中图分类号：TV122

文献标志码：A

文章编号：0493-2137（2016）04-0400-08

DOI:10.11784/tdxbz201503066

收稿日期：2015-03-23；修回日期：2015-08-10.

基金项目：国家自然科学基金创新研究群体科学基金资助项目（51021004）；河北省水利科研计划资助项目（HS2007-43）.

作者简介：李大鸣（1957— ），男，教授.

通讯作者：李大鸣，lidaming@tju.edu.cn.