矩阵向量相乘的并行算法分析

雷耀明

【摘 要】 大规模矩阵向量相乘是数值代数中常用的科学计算方式。其维数增大而造成的计算量增大是计算科学中需要进一步解决的问题。本文基于矩阵向量不同模式下的计算，给出算法的分析与实现。

【关键词】 并行计算 矩阵相乘 MPI

一、问题背景

矩阵是数学以及工程中的一个基本概念，许多科学计算问题往往归结为对矩阵的操作，如三维图像处理、神经网络等。由于矩阵的运算，特别是大规模矩阵相乘，矩阵的特征值求解等需要大量内存并且耗时的处理过程，单处理机已经无法承受，因此有效地实现大型的矩阵并行算法在实际应用中是非常重要的。

二、大规模矩阵向量相乘的串行算法描述

设A和B是两个n×n矩阵，将矩阵A和B的乘积记为C=B×A，那么C也是一个 n×n矩阵，乘积C的第i行第j列的元素等于A的第i行和B的第j列对应的元素乘积的和，可表示为C（i，j）=，特殊地，当考虑矩阵B为矩阵向量。采用串行算法在传统计算机上计算矩阵乘法时，需要使用比较多的工作单源和存储单元，计算A和B的乘积的结果矩阵C时，每计算出C的一个元素，需要做n 次乘法和n-1次加法， 逐项计算个共需执行（n-1）次加法和次乘法，计算效率将受到很大的影响。

串行算法：

三、 模型建立

3.1矩阵相乘按行计算

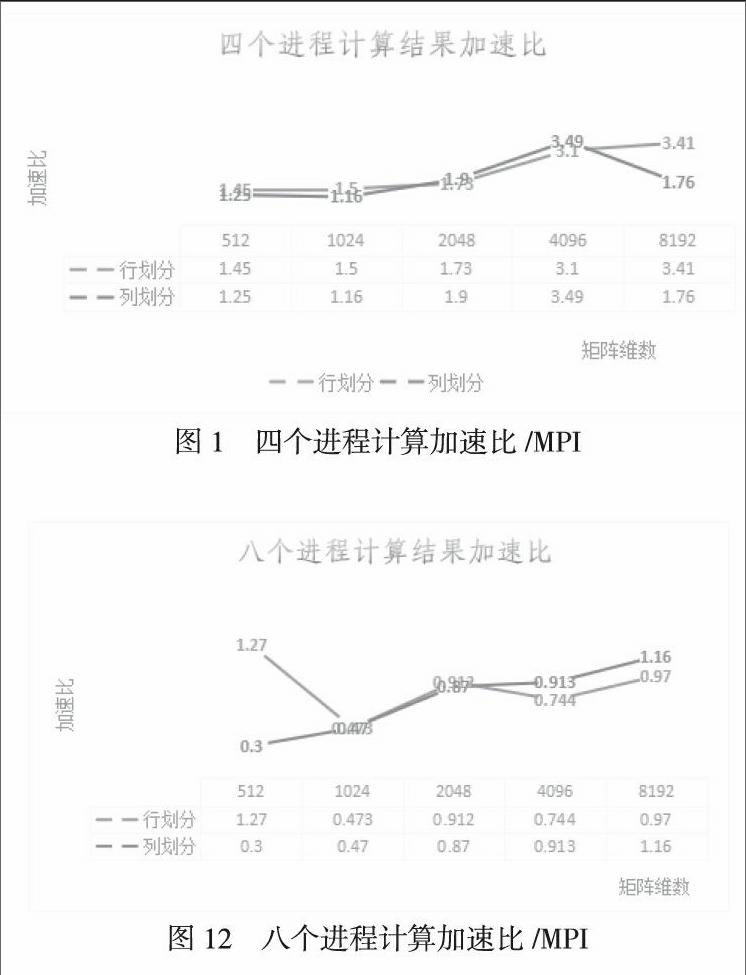
特殊地，考虑B矩阵为，矩阵向量相乘时，我们考虑nxn维矩阵A在n个进程间划分的情况。将计算机进程编号为，0，1，2…n-1 。则每一个进程都会存储1xn维矩阵。进程会存ai1，ai2，ai3…ain。并且负责计算。向量C的存储方法与B相同。考虑P（p

3.2 矩阵相乘按列计算

按列进行划分是对每一行进行划分然后发送到每个进程上。我们考虑0，1，2…n维矩阵A在n个进程间划分的情况。将计算机进程编号为0，1，2…n-1。对于矩阵的第一行，a11…a1n进行划分，进程pi接收到元素的为ai1，每一行划分后，进程pi接收到的元素为a1i…ani。进程pi做的计算为cj=aji×bi，j=1…n； 每一个进程都会得到一个向量，将每一个向量所对应的元素相加，即得到最终的向量c。

3.3 基于MPI的多核并行算法的设计

MPI是一种基于信息传递的并行编程技术。主进程按行划分矩阵及向量，记录自身计算所需矩阵分量并调MPI_Send将向量发给各个进程；其余进程调用 MPI_Recv接收主进程发送的矩阵分量及向量分量； 各个进程调用MPI_Scatter按行共享主进程中的矩阵；各个进程进行矩阵向量相乘；各进程调用MPI_Gather将所有向量各个分量聚集到主进程上得到最终结果。

四、数值实验和结论

MPI结果图表分析：

（1）随着矩阵规模的不断增大，程序的执行时间中，计算时间占主导因素，并行计算的优势得到了体现，运行时间随着进程数的增加而逐渐减少。

（2）两种分发方式中，随着维数的增高，按行划分是相对有效的方法。按列划分在分发时需要分发的次数为维数的倍数，分发的时间将大大增加。按列划分需要将矩阵进行块划分。然后再进行分发，相对来讲，增大了时间的消耗。

（3）随着矩阵规模的不断增大，使用并行计算的运算时间远小于串行算法的运算时间，在大规模矩阵的运算过程中，并行计算有很大的优势.

【参考文献】

[1] 多线程并行快速求解e 值的六种方法，朱建伟，刘荣.研究与开发.

[2] 多核系列教材编写组.多核程序设计[M].北京.清华大学出版社，2007.

[3] 周灿，杨小帆.矩阵乘法的并行算法研究分析.计算机应用研究.