初始裂缝对重力坝地震响应特性的影响

王 超，张社荣 3，王高辉

（1. 河海大学水文水资源与水利工程科学国家重点实验室，南京 210098；2. 天津大学建筑工程学院，天津 300072；3. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；4. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）



初始裂缝对重力坝地震响应特性的影响

王 超1 2，张社荣1 2 3，王高辉4

（1. 河海大学水文水资源与水利工程科学国家重点实验室，南京 210098；2. 天津大学建筑工程学院，天津 300072；3. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；4. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

摘要：初始裂缝对重力坝抗震安全性的影响不可忽视，甚至成为控制结构安全储备和破坏模式的关键因素.将水平集方法应用到初始裂缝界面的描述及加强单元类型的判别，并与扩展有限元相结合，通过在相关节点的影响域上富集非连续位移模式，描述裂缝的扩展.基于扩展有限元算法研究了不同位置深度和倾角的初始裂缝对重力坝地震全过程中动力性态、最终破坏模式和缝面动力行为的影响.结果表明：坝顶水平向位移波动幅值、缝面的张合及最终滑移状态均随着初始裂缝深度的增大而增大；初始缝倾角并不作为坝体最终破坏模式的控制因素，坝体的最终破坏形态主要受坝体在地震作用中的应力场条件控制；倾斜向上初始缝一定程度上抑制了开裂路径的发展，对坝体的地震危害最小.

关键词：重力坝；初始裂缝；扩展有限元法；水平集方法；动力行为

多年来，各种理论一直在均匀介质假设基础上研究其破坏规律，较少涉及材料自身含有初始缺陷等非均质特性对混凝土结构特性和力学性能的影响.然而，作为一种多相复合的准脆性材料，由于混凝土材料制备、施工过程、大体积混凝土内外温差、混凝土干缩等作用，大体积混凝土结构普遍存在以裂缝为主要表现形式的初始缺陷［1］，工程结构的失稳与这些裂缝的扩展、贯通密切相关.大量监测资料表明，运行中的重力坝或多或少几乎都存在不同程度的裂缝［2］，因此，初始裂缝是混凝土结构客观存在的真实条件.修建在我国西南强震区的重力坝一旦遭遇地震作用，初始裂缝等缺陷对结构动力响应规律有怎样的影响，是目前工程界的一个不可回避的现实问题，甚至成为控制结构安全储备和破坏模式的关键因素.

含初始裂缝重力坝破坏过程的研究方面，Carpinteri等［3］、Renzi等［4］、Barpi等［5］分别基于物理模型手段进行了破坏试验，而在数值模拟方面，最为有效的数值方法就是Belytschko等［6］提出的分析不连续性问题的扩展有限元法（extended finite element method，XFEM）.该方法通过在相关节点的影响域上富集非连续位移模式，把诸如裂纹、节理等非连续性结构嵌入到单元内部，使得在进行非连续性结构（比如裂纹扩展）的演化计算时无须网格重剖分，然而早期的 XFEM 只能分析简单的平面问题，裂纹多是规则形状，且为单裂纹；随后许多学者对该方法在裂缝界面描述和追踪方面进行了改进：例如Sethian［7］将水平集方法（level set method）应用到裂缝界面的描述，并与扩展有限元相结合，从而可以分析较为复杂裂缝界面的问题；Stolarska等［8］将水平集与扩展有限元相结合模拟了裂纹的扩展，采用水平集函数追踪裂纹，扩展有限元进行数值计算；Sukumar等［9］在扩展有限元的框架内结合水平集法，模拟了材料内含孔洞的问题；茹忠亮等［10］结合水平集与XFEM研究了裂尖积分区域对应力强度因子计算精度的影响；张社荣等［11］采用XFEM有效地分析了大坝地震渐进破坏过程和失效模式问题.

鉴于目前对含有初始裂缝重力坝在地震作用下的动力性态研究较少，本文将水平集算法应用到初始裂缝界面的描述及加强单元类型的判别，并与扩展有限元相结合，对动力作用下的含初始裂缝的重力坝开裂破坏行为进行数值分析，探讨初始裂缝不同位置因素和深度因素对结构动力响应规律的影响，预测坝体初始裂缝在各种可能条件下的扩展路径，为工程抗震措施的制定提供依据.

1　扩展有限元及水平集函数

XFEM由Belytschko等［6］基于单位分解的思想对传统有限元法进行了改进后首次提出，该方法基于整体划分的概念，属于传统有限元方法的扩展.其基本的思想是用一些附加函数来改进传统有限元，使得裂缝几何独立于计算网格，扩展函数通常包括裂纹尖端附近渐进函数（用于模拟裂纹尖端附近的应力奇异性）及间断函数（用于表示裂纹面处位移跳跃）.本文中的XFEM是基于ABAQUS软件实现的.

1.1扩展有限元的位移模式

XFEM中，通过附加函数加强常规有限元逼近模拟裂纹的扩展.扩展有限元的位移逼近可表示为

式中：右端第1项可用于模型中所有节点；右端第2项、第3项、第4项为XFEM特有的，称为加强项，用来描述裂纹的存在；Ni为节点i的形函数；ui为节点i位移向量的连续部分；bj为结点j与阶跃函数相关的节点加强自由度；分别为两个裂尖处与弹性渐进裂尖函数有关的节点加强自由度；H（x）为沿裂纹面的间断阶跃函数；（m= 1，…，4）为裂纹尖端应力裂尖函数.

在线弹性断裂力学中，裂纹尖端位移场可用水平集函数构造的裂尖函数Fi（r θ）表达，即

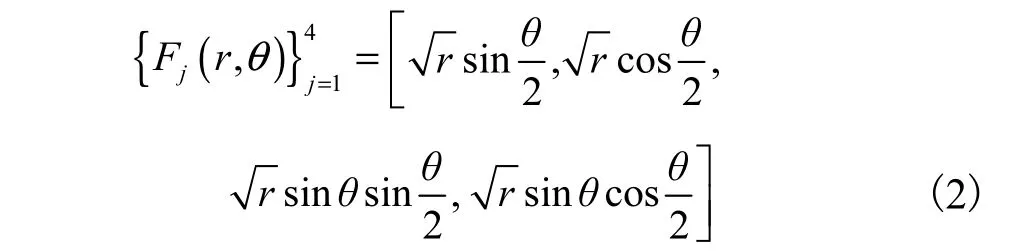
式中r和θ为裂纹尖端为坐标原点、裂纹外切线为极轴的局部极坐标，θ=0表征裂纹尖端切线方向.位移模式构造后，由虚功原理推导扩展有限元的支配方程.

需要说明的是，扩展元的位移模式及支配方程建立的详细过程可参见文献［11］，本文不再赘述.

1.2用水平集函数描述初始裂缝

水平集方法是一种用于界面追踪和形状建模的数值技术，裂缝界面可以通过定义比界面高一维的零水平集函数来表示［12］.一般用两个水平集描述裂缝，一是裂缝面水平集ϕ（x），其零水平集为裂缝界面；二是波前水平集φ（x），用于描述裂缝尖端沿开裂平面方向上的距离，二者相互正交.在有限元数值模拟中，网格上裂缝的局部特性是通过增加附加函数来描述的，网格剖分时不需考虑裂缝位置.初始裂缝的位置由裂缝面端点的坐标和直线方程参数确定.

式中：t′表示单位切向矢量；xi为裂尖坐标.

通过定义上述两个水平集函数，初始裂缝可描述为ϕ=0， φ＜ 0.

裂缝扩展以后，有限元网格不需要重剖分，只需要更新裂缝的端点坐标和方程参数，在扩展有限元的位移模式中，将单元划分为常规单元和加强单元（包括完全贯穿单元、裂尖单元）.为了准确判别加强单元的类型，水平集方法通过各单元水平集函数值来判别加强单元的类型，判别准则如下：①如果，此单元为常规单元；② 如果ϕmax＜ 0且，则裂缝完全贯穿该单元，需通过H（ x）跳跃函数加强节点的自由度；③ 如果单元区内，则该单元为裂尖单元，单元内节点通过裂尖渐进位移场附加函数jϕ加强节点的自由度.其中，ϕmin、ϕmax和φmin、φmax分别是单元各水平集（裂缝面水平集和波前水平集）的最小值和最大值.

2　算例验证

对Carpinteri等［3］所做的含初始裂纹重力坝试验应用XFEM进行数值模拟计算.模型参数如下：长度比尺为1∶40；初始裂缝长度为150 mm.模型厚度都为300 mm.通过模拟2 000 kN的推力施加在上游面来模拟静水压力，静水压载荷被分布在4个集中加载点上，每个加载点的荷载大小分别为总荷载大小的43.75% 、31.25% 、18.75% 、6.25% ，如图1（a）所示.材料的起裂断裂韧度值近似取为0.8 mPa·m1/2.混凝土材料弹性模量E为35.7 GPa，泊松比为0.1，材料断裂能为0.184 N/mm，抗拉强度3.6 mPa，密度2 400 kg/m3.

本文建立的含初始裂缝的数值模型见图1（b），为了更为准确地描述初始裂缝的发展方向角度，数值模型在裂缝部位进行了网格加密.在对应的集中荷载及自重作用下，结合水平集函数和扩展有限元法进行裂纹界面的追踪，可以发现，数值分析结果（见图2）与模型试验结果比较吻合，且优于黏聚裂缝模型的仿真结果（见图3），说明本文方法对初始裂缝及其扩展过程的模拟是有效的.

图1　数值验证所用的Carpinteri 模型Fig.1 Carpinteri modal for numerical validation

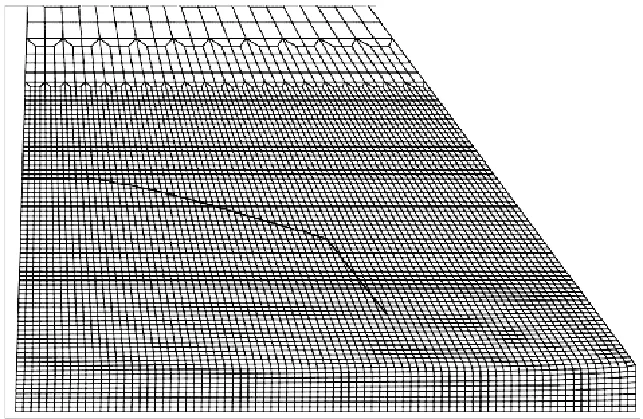
图2　数值分析结果Fig.2 Numerical results

图3　不同方法仿真结果与试验结果的对比Fig.3 Contrast between test and simulation results of different methods

3　工程实例分析模型及条件

3.1计算模型及条件

某碾压混凝土重力坝，挡水坝段建基面高程为1 192.00 m，正常蓄水位1 330.00 m，坝顶高程为1 334.00 m，坝前泥沙淤积高程1 211.10 m（淤沙浮容重为6.0 kN/m3，内摩擦角为12°），相应下游水位1 203.70 m.坝体典型体型如图4所示，碾压混凝土分区材料参数见表1.其中，混凝土材料的断裂能密度参考文献［8］和文献［11］的相应标号混凝土材料的断裂能参数选用.坝址区水平向地震峰值加速度（100年超越概率2%）设计值为0.284 g，相应的校核值为0.344 g.

计算中，混凝土本构采用塑性损伤模型，碾压混凝土材料密度2 400 kg/m3，泊松比 0.2，动态弹模及抗拉、压强度见表1.计算网格在坝颈部分局部加密.地基模型采用无质量弹性地基进行模拟，岩体动弹模暂取静态值.弹性模量18 GPa，泊松比0.22，抗剪断参数f=1.12，c=1.40 mPa.模型底部考虑全约束，左右边界法向约束.

数值计算中，荷载组合为：上游正常蓄水位水压力+下游相应尾水位水压力+坝体自重+上游淤沙压力+坝基面扬压力+地震荷载.

表1　大坝混凝土的参数Tab.1 Parameters of the concrete

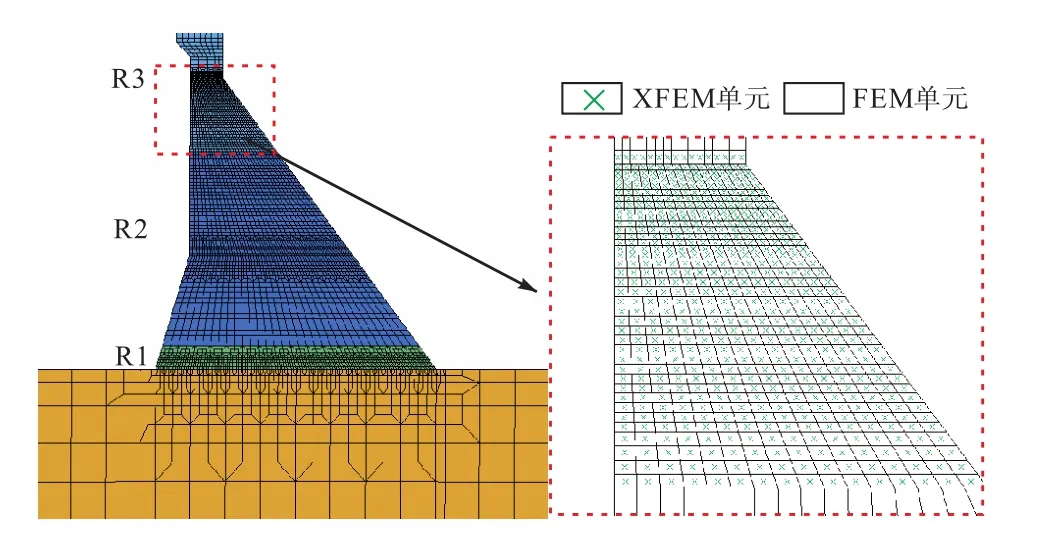
图4　坝体体型及其模型Fig.4 Section and modal of the dam

3.2地震动选取

在动力计算中，地震动采取顺水流向和竖向同时由地基输入，动水压力采用Westergaard公式计算，Rayleigh阻尼因数根据线弹性分析得到的前两阶频率计算.本次计算中选用经典的Koyna波，水平向峰值加速度按照校核烈度值0.344g调幅，竖向地震波峰值取水平向的2/3.地震荷载采用1967年的Koyna地面实测地震波，如图5所示.

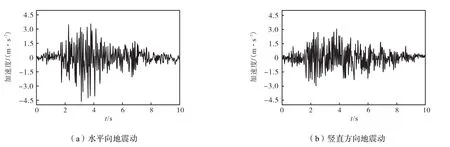
图5　Koyna地震波Fig.5 Koyna earthquake wave

4　初始缝对坝体动力破坏的影响分析

初始裂缝的位置和倾角是影响开裂破坏模式的两个重要的参数，由于外部环境条件或施工等人为不确定性因素的影响，裂缝的深度及位置表现出一定的随机性.实际坝体上的裂缝不可能都是水平状的，有些裂缝会呈现一定的角度，因此，本节主要探讨不同位置和倾角的裂缝对重力坝动力性态的影响问题.

坝头位置是地震作用下重力坝结构的薄弱部位.为说明问题，本文选取坝体坝头位置上下游处的代表性初始裂缝，研究其对重力坝动力性态的影响.需要说明，计算中不考虑水流渗入裂缝引起的坝体内渗流场的变化.

含不同初始裂缝的坝体剖面如图6所示，拟定以下6种情况进行数值模拟：①情况1，无初始缝的情况；②情况2，下游侧水平0.5 m初始缝C2；③情况3，下游侧水平1.0 m初始缝C3；④情况4，下游侧水平向上45°深0.5 m缝C4；⑤情况5，下游侧水平向下45°深0.5 m缝C5；⑥情况6，下游侧水平0.5 m初始缝C1+上游侧水平0.5 m初始缝C6.

在此次乌镇峰会上，“数字经济”再一次成为所有专家学者、企业家以及资本管理者眼中的热点。如果说互联网的上半场是信息的全球互联与共享，那么下半场则是工业互联网的未来。显而易见，在数字时代，传统工业面临着一场更彻底的转型。国家信息化专家咨询委员会常务副主任周宏仁在演讲中说：“广大的中国企业，特别是中小企业的数字转型，既是中国发展数字经济极好的机遇，也是中国发展数字经济所面临的紧迫而严峻的挑战。”

图6　含不同初始裂缝的坝体剖面Fig.6 Dam profile with different initial cracks

4.1坝体动力响应性态

采用扩展有限元方法研究坝体动力响应特性.在强震荷载作用下，重力坝的关键部位的拉-压循环应力状态对混凝土材料非常不利，部分混凝土会产生损伤和弱化.在Koyna实测地震波作用下，对不同初始裂缝模型，坝顶上游角点P1（见图6）水平位移时程曲线如图7所示.

由图7（a）可以看出，在初始裂缝没有发生进一步的扩展（t=3.86 s）之前，不同长度的初始裂缝对坝顶位移的影响不大，但随着地震作用峰值的出现，坝顶水平向位移波动幅值随着初始裂缝深度的增大而增大.

在图7（b）中，不同情况下坝顶水平位移在整个时间历程中并没有明显的规律性，但在初始裂缝开始扩展的时刻（t=3.86 s），仍表现出了初始缝倾角对坝体开裂的限制作用，即含有斜向上倾角初始缝（情况4）的坝体水平向位移最小，水平缝（情况2）的情况次之，含斜向下初始缝的情况（情况5）坝体水平向位移最大.也就是说，情况5条件下，裂缝的发展路径和方向更加自由，可以迅速沿着应力场中的最薄弱方向发展，且在地震作用的末期（t=8～10 s）仍表现出较大的水平位移波动幅值；而当初始裂缝斜向上倾斜时，裂缝的进一步扩展被限制.

上下游同时含有初始缝情况（情况6）下，坝顶水平位移在整个时间历程中波动幅度最大且波动周期缩小（见图7（c）），说明该情况下坝体破坏最为严重，开裂扩展最为迅速.

图7　不同情况下坝顶上游角点P1点水平位移时程曲线Fig.7 Horizontal displacement curve of P1under different calculation schemes

4.2初始缝扩展路径及破损模式分析

基于水平集理论及扩展有限元算法，采用最大拉应力准则并假定扩展过程中裂纹尖端位于单元边界上，得到Koyna实测地震波作用下的大坝最终失效模式.图8给出了坝体在含有不同初始裂缝情况下的扩展路径及最终破坏形态.

对比上述多种工况的破坏模式，无论初始裂缝倾向上游或下游，裂缝如果发生扩展，最终均会逐渐发展成为一条倾向上游的倾斜裂缝，这说明，初始裂缝倾角并不作为坝体最终破坏模式的控制因素，坝体的最终破坏形态主要受坝体在地震作用中的应力场条件控制.

图8　不同初始裂缝情况下的裂缝扩展路径及坝体最终破坏形态Fig.8 Crack propagation paths and dam failure patters under different cases of initial cracks

4.3裂缝行为分析

初始裂缝在地震作用过程中的缝面张合和滑移行为是评价裂缝动力性态的重要内容.本节在扩展有限元分析结果的基础上，对不同初始裂缝在地震过程中的动力行为进行分析.

4.3.1缝面张合行为

图9给出了不同情况下地震作用过程中初始裂缝缝面的张合行为.

图9　不同情况下地震作用过程中初始裂缝缝面的张合行为Fig.9 Joint behavior of the initial crack during the whole seismic process

从图9可以看出以下3点.

（1）不含初始缝的坝体开裂后，在地震作用过程中，情况1缝面的最大张开位移为5.97 mm，远小于情况2下的张开位移15.32 mm和情况3下的张开位移35.62 mm.结果表明，坝头下游侧水平初始缝越深，在地震时程中缝面的张开幅值就越大.

（2）对于不同倾角的初始缝，其缝面的张合行为受倾角的影响较大.情况5下，缝面张开幅值最大，达到34.81 mm，而情况4下，缝面张开幅值仅为5.17 mm，这与坝顶水平向位移所反映出的结果一致.

（3）对于情况6，下游侧初始缝面张合最大幅值为15.57 mm，且在地震历程的末期，缝面张合行为波动幅度仍然较大.

4.3.2缝面滑移行为

图10给出了不同情况下初始裂缝缝面滑移行为.从图10中可以看出以下3点.

（1）不含初始缝的坝体开裂后，在地震作用的整个时间历程中，情况1条件下缝面的最终滑移位移为0.11 mm，小于情况2下的滑移位移0.25 mm和情况3下的滑移位移0.40 mm.结果表明，坝头下游侧水平初始缝越深，最终的缝面滑移就越大.

（2）对于不同倾角的初始缝，其缝面的滑移行为受倾角的影响较大.情况5条件下，缝面最终滑移最大，达到0.86 mm，而情况4下，缝面最终滑移仅为0.28 mm.

（3）对于同时含有上游和下游初始缝（情况6）条件下，下游侧初始缝面最终滑移位移最大，达到6.95 mm，且在地震历程的末期，缝面滑移行为波动幅度仍然较大.

图10　不同情况下初始裂缝缝面滑移行为Fig.10 Slip behavior of the initial crack under different calculation schemes

5　结 论

（1）初始裂缝的深度和倾角参数均会影响地震过程中坝顶的水平向位移幅值.其中，初始缝倾角斜向上的坝体最终水平向位移最小；初始缝倾角斜向下时，裂缝的发展路径和方向更加自由，可以迅速沿着应力场中的最薄弱方向发展，因而坝体最终水平向位移最大.

（2）坝体在地震作用中的应力场条件仍是坝体最终破坏形态的主要控制因素，初始裂缝倾角并不作为坝体最终破坏模式的控制因素.下游侧斜向上的初始缝在一定程度上限制了裂缝向上游侧贯穿破坏的趋势，这种形态的初始裂缝危害最小.

（3）坝头下游侧水平初始缝深度越大，在地震时程中缝面的张开幅值和最终的缝面滑移就越大；同时，初始裂缝在地震作用下的缝面张合滑移行为受倾角的影响较大.

需要说明的是，实际工程中裂缝面内部水压力作用机理比较复杂且上下游坝面的裂缝不止一条（如震后），因此，考虑裂缝面水力劈裂问题并研究上下游坝面多裂缝组合模式下重力坝结构的开裂破坏模式，将是下一步研究的重点.

参考文献：

［1］ 杜效鹄，段云岭，王光纶. 重力坝断裂数值分析研究［J］. 水利学报，2005，36（9）：1035-1042. Du Xiaohu，Duan Yunling，Wang Guanglun. Numerical analysis of fracture in gravity dam ［J］. Journal of Hydraulic Engineering，2005，36（9）：1035-1042（in Chinese）.

［2］ 王志远. 重力坝的实测坝踵应力及原因分析［J］. 大坝观测与土工测试，2001，25（1）：4-6. Wang Zhiyuan. Observed stresses in dam heel and analysis of causes ［J］. Dam Observation and Geotechnical Tests，2001，25（1）：4-6（in Chinese）.

［3］ Carpinteri A，Valente S，Ferrara G，et al. Experimental and numerical fracture modeling of a gravity dam ［C］// Fracture Mechanics of Concrete Structures. Amsterdam，Netherlands，1992：351-360.

［4］ Renzi P，Ferrara C，Mazza G. Centrifuge in a concrete gravity dam：A centrifugal investigation ［C］// Proceedings of the International Workshop on Dam Fracture and Damage. Chambery，France，1994：103-109.

［5］ Barpi F，Valente S. Size-effects induced bifurcation phenomena during multiple cohesive crack propagation ［J］. International Journal of Solids and Structures，1998，35（16）：1851-1861.

［6］ Belytschko T，Black T. Elastic crack growth in finite elements with minimal remeshing ［J］. International Journal for Numerical Methods in Engineering，1999，45（5）：601-620.

［7］ Sethian J A. Level Set Methods and Fast Marching Methods：Evolving Interfaces in Computational Geometry，Fluid Mechanics，Computer Vision，and Materials Science ［M］. UK：Cambridge University Press，1999.

［8］ Stolarska M，Chopp D L，Moës N. Modeling crack growth by level sets in the extended finite element method ［J］. International Journal for Numerical Method in Engineering，2001，51（8）：943-960.

［9］ Sukumar N，Choop D L，Moës N，et al. Modeling holes and inclusions by level sets in the extended finiteelement method ［J］. Computer Methods in Applied Mechanics and Engineering，2001，190（14）：6183-6200.

［10］ 茹忠亮，朱传锐，赵洪波. 基于水平集算法的扩展有限元方法研究［J］. 工程力学，2011，28（7）：20-26. Ru Zhongliang，Zhu Chuanrui，Zhao Hongbo. Study on the extend finite element method based on lever set algorithm［J］. Engineering Mechanics，2011，28（7）：20-26（in Chinese）.

［11］ 张社荣，王高辉，孙 博，等. 基于扩展有限元法的重力坝强震潜在失效模式分析 ［J］. 水利学报，2012，43（12）：1431-1439. Zhang Sherong，Wang Gaohui，Sun Bo，et al. Seismic potential failure mode analysis of concrete gravity dam based on extended finite element method ［J］. Journal of Hydraulic Engineering，2012，43（12）：1431-1439（in Chinese）.

［12］ van der Meer F P，Moës N，Sluys L J. A level set model for delamination—Modeling crack growth without cohesive zone or stress singularity ［J］. Engineering Fracture Mechanics，2012，79（1）：191-212.

（责任编辑：樊素英）

Influence of Initial Cracks on Seismic Response Characteristics of Gravity Dam

Wang Chao1 2，Zhang Sherong1 2 3，Wang Gaohui4
（1. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing 210098，China；2. School of Civil Engineering，Tianjin University，Tianjin 300072，China；3. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；4. State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China）

Abstract：As the main form of initial defects the influence of cracks cannot be ignored specially and even may become the critical factor of structure safety and its failure modes. The level set method is employed to describe the initial crack interface and judge the element types. Based on both extended finite element method （XFEM）and lever set method （LSM） it is carried out that the crack extension by enrichment of discontinuous displacement mode on the node domain. Moreover the influence of initial cracks on the gravity dam is studied including its position depth and dip angle. Then the effects of initial cracks are discussed which is on the crack propagation and seismic response of the concrete gravity dam during the whole process of earthquake. The results show that: the displacement amplitude of dam crest the size of opening and closing of the cracks and the slippage increase with the increase of initial crack depth； the controlling factor of dam final failure mode and ultimate failure pattern is not the dip angle of the initial cracks but the stress field condition； inhibiting effect on the crack propagation appears when the initial cracks have upward angle so that small earthquake hazards will be produced to the dam body.

Keywords：gravity dam；initial crack；extended finite element method；level set method；dynamic behavior

中图分类号：TV312

文献标志码：A

文章编号：0493-2137（2016）04-0392-08

DOI:10.11784/tdxbz201409061

收稿日期：2014-09-23；修回日期：2014-11-24.

基金项目：国家创新研究群体科学基金资助项目（51321065）；天津市应用基础与前沿技术研究计划青年项目（15JCQNJC08000）；河海大学水文水资源与水利工程科学国家重点实验室开放基金资助项目（2014491211）.

作者简介：王 超（1986— ），男，博士，讲师，wangchaosg@tju.edu.cn.

通讯作者：张社荣，tjuzsr@126.com.