点蚀损伤船体板格单轴压缩极限强度

张 岩，黄 一

（1. 哈尔滨工业大学（威海）船舶与海洋工程学院，威海 264209；2. 大连理工大学船舶工程学院，大连 116024）



点蚀损伤船体板格单轴压缩极限强度

张 岩1，黄 一2

（1. 哈尔滨工业大学（威海）船舶与海洋工程学院，威海 264209；2. 大连理工大学船舶工程学院，大连 116024）

摘要：为了能够简单准确地计算服役期内点蚀损伤船体板格的极限强度，选择腐蚀体积为点蚀损伤板的主要评估参数，结合实际船体板格的腐蚀损伤特点，采用有限元数值计算方法，分析点蚀坑形状、有限元单元类型、蚀坑分布和蚀坑深度对板极限强度的影响，以及板的初始柔度、初始变形、长宽比和板边缘线性载荷因子对板极限强度折减因子的影响，并利用回归分析方法，建立了基于腐蚀体积的点蚀损伤船体板格极限强度折减因子的计算公式.结果表明，整套公式的计算结果与有限元计算结果的相对误差仅有极少量在5% ～6% 之间，绝大部分在5% 以内，可用于服役期内点蚀损伤船体板格的安全评估.

关键词：极限强度；点蚀；腐蚀体积；船体板格；单轴压缩

网络出版时间：2015-09-28. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20150928.1554.004.html.

点腐蚀损伤是船体板格中较常见的损伤形式，其损伤形态较为复杂，对船体结构极限强度造成的影响较大.船体板格结构中大部分主要承受总纵弯曲应力，即作用在板格上的载荷以单轴向压缩为主，本文研究点蚀损伤船体板格在单轴压缩下的极限强度计算问题.

对于点蚀损伤船体板格在单轴压缩下的极限强度计算问题，国外学者从20世纪50年代开始研究，国内学者从21世纪初开始涉及这方面研究.较有代表性的研究有Sadovský等［1］利用试验数据通过统计方法得到局部腐蚀板条临界屈曲载荷.Paik等［2］提出了基于最小横截面积的点蚀板极限压缩强度的精确设计公式.Dunbar等［3］结合有限元模拟分析与试验手段，讨论了方板中间有腐蚀时对稳定性的影响.Nakai等［4-6］对局部存在点蚀的散货船典型构件的极限强度进行了一系列试验与有限元分析，得出极限强度与点蚀分布、点蚀位置和板厚有关；有规则点蚀板的极限强度略小于或几乎等于均匀腐蚀板的极限强度.Ok等［7-8］针对在板边区域有腐蚀的两种情况，用256个非线性有限元计算结果得到了预测局部腐蚀非加筋板极限强度的经验公式.江晓俐等［9-10］通过点腐蚀板的非线性有限元分析，指出点腐蚀密集度对于板极限承载能力有主要和直接的影响，单侧点腐蚀引起的偏心对板的极限抗压能力有显著影响.

已有研究多为定性分析或仅适用于特定情况的经验公式，尚未形成公认的可应用于工程分析的量化计算方法.已有文献表明可通过实船船体腐蚀检测数据直接得到腐蚀体积［11］；Huang等［12-13］则已经提出了用腐蚀体积为参数来计算点蚀损伤板的极限强度.但是已有的分析注重方法的验证，考虑的影响因素不全面，且分析的板格为两面有相同腐蚀损伤的板格.由于船体所处的环境较为复杂，船体板格发生腐蚀损伤后，其板格两面所处的腐蚀环境可能相差较大，因此将导致板格两面的腐蚀情况不同，会产生偏心问题.船体板格为薄板，当板格两面腐蚀损伤情况相差很大时，可简化为仅有一面有腐蚀损伤的情况，这在船体板格中较为常见.

鉴于以上分析，本文主要研究遭受点蚀损伤船体板格仅一面有腐蚀损伤情况时，在单轴压缩载荷作用下的极限强度计算问题，得到可以在实际工程分析中应用的点蚀损伤船体板格极限强度计算公式.

1　点蚀损伤板极限强度影响因素分析

对于点蚀损伤板，无法用解析法求出精确解，多采用经验公式或数值计算方法.本文将在已有分析的基础上，采用数值计算方法对点蚀损伤板的极限强度进行计算.

由于影响板极限强度的因素有多个，因此在开展大量计算前，要先分析在用腐蚀体积为参数计算极限强度时，各主要因素对极限强度的影响.

1.1数值计算模型基本参数设定

本文所有计算模型的设定均基于船体结构板格，基本参数设定如下.

（1）板的宽度.为了简化计算，本文计算模型中板的宽度采用同一数值，取船体板格中较为常见的尺寸，即b=750 mm，且单轴向载荷均作用于板宽边.

（2）板的弹性模量E、泊松比v和屈服应力σs.船体结构目前大多采用高强度钢，其材料参数取为：E=2.06×105MPa，ν=0.3，σs=315 mPa.

（3）板的焊接残余应力.实际船体结构板格的焊接残余应力较难准确确定，笔者根据已有研究成果［14-15］，取较为理想的残余应力情况，见图1及式（1）.

图1　板格残余应力分布Fig.1 Distribution of residual stress of the plates

式中：a为板的长度（沿x轴方向）；b为板的宽度（沿y方向）；at和bt表示残余应力作用长度（见图1）；σrtx、σrcx、σrty和σrcy为残余应力（见图1）；σs为屈服应力.

（4）板的边界条件.根据文献［17］的分析，船体结构中的板格可以简化为四边简支且保持直线的边界条件.

（5）点蚀坑.已有研究［4］表明散货船中点蚀坑（本文中简称蚀坑）为圆锥形，直径与深度的比值为10∶1～8∶1；油船中点蚀坑为半圆球形，直径与深度的比值为6∶1～4∶1.大量实船检测数据［11］显示，点蚀坑的最大直径一般小于80 mm.在船体检测中规定［11］，许用最大平均厚度为原厚度的50% ，许用最大点蚀面积为原板面积的30% .结合上面的分析，设定蚀坑直径d=0～80 mm，蚀坑深度h=0～0.5 t0mm（t0为板初始厚度），点蚀面积百分比（点蚀面积与板面积的比值）Ap=0～25% .

船体结构板格的一侧表面通常处在同一腐蚀环境体系中，而大量检测结果表明点蚀坑在板上的分布近似于均匀分布［2］.据此本文设定的点蚀坑亦近似均匀分布在板上.

1.2蚀坑形状对极限强度的影响

虽然船体结构板上点蚀坑的形状多为圆锥形或半圆球形，但是这两种形状蚀坑的数值计算模型较为复杂，不易于进行大量数值计算分析.因此，本文将采用较简单的圆柱形点蚀坑来代替圆锥形及半圆球形点蚀坑，同时保证简化后的点蚀坑体积与原点蚀坑体积相同，并分析这种简化对极限强度计算的影响.

为了进一步简化计算，设定模型中点蚀坑具有相同的直径，蚀坑分布情况见图2.

图2　蚀坑分布Fig.2 Distribution of pits

模型的长a=750 mm，初始厚度t0=12 mm，初始变形形态设定与特征值屈曲分析的第一阶屈曲模态相同，最大面外位移取为0.05β02t0（β0为无腐蚀损伤时板的柔度）.蚀坑参数如表1所示，其他参数与第1.1节中的设定相同.

表1　蚀坑形状参数Tab.1 Shape parameters of pits

经计算得出具有圆柱形蚀坑、半圆球形蚀坑以及圆锥形蚀坑的板模型受载边缘的平均应力-平均应变曲线见图3，其曲线的峰值应力即为板的极限强度，其值分别为175 mPa、174 mPa和175 mPa.结果表明，在腐蚀体积相同的情况下，点蚀坑的形状对点蚀损伤板模型的极限强度影响很小，这样在有限元数值计算中，可以将圆锥形蚀坑及半圆球形蚀坑简化成具有相同体积的圆柱形蚀坑.

图3　3种具有不同形状蚀坑的板模型的平均应力-平均应变曲线Fig.3 Average stress-average strain curves of three kinds of plates with different shape pits

1.3有限元单元类型对极限强度的影响

针对第1.2节中得出的结论，本节假定蚀坑为圆柱形，考虑用壳单元代替体单元建立点蚀损伤板的有限元模型，实施极限强度计算，并对计算结果进行比较分析，以便进一步简化有限元计算.

计算模型的基本参数设定与第1.2节中的相同，板模型见图4，在有限元模型建立中，蚀坑及其附近采用映射网格划分方法，其他区域尽量采用规则网格划分.

图4　板模型Fig.4 Models of the plate

用壳单元和体单元分别建立如图4所示板模型的有限元模型，计算得到的模型受载边缘的平均应力-平均应变曲线见图5.图5显示2种单元计算得到的平均应力-平均应变曲线在极限强度到达前变化趋势基本一致，极限强度到达后有所不同，但用壳单元和体单元计算得到的极限强度分别为157 mPa和159 mPa，数值非常接近，表明可采用壳单元建立点蚀损伤板有限元模型来开展极限强度分析.

1.4蚀坑分布对极限强度的影响

由于船体结构板的蚀坑分布具有随机性，在开展大量模型的极限强度分析时，对不同蚀坑分布情况建立有限元模型将花费很多时间，因此本节分析蚀坑有规律分布的板和蚀坑随机分布的板的极限强度，寻求更简化的蚀坑分布模型的建立方法.

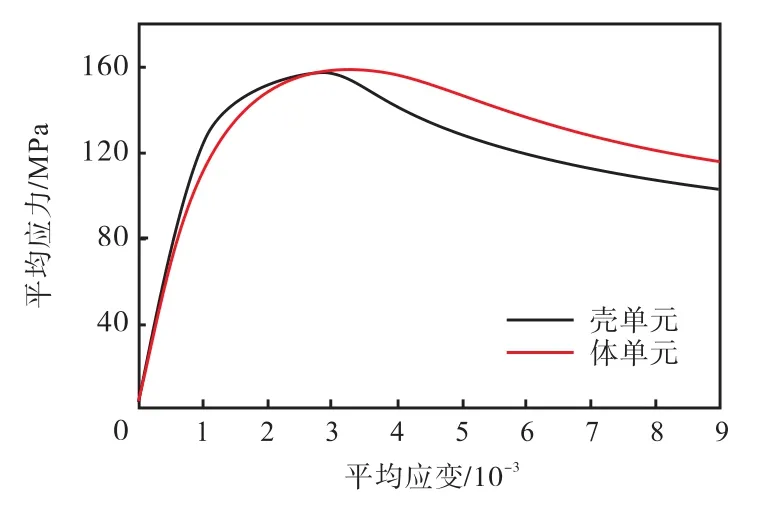
图5　两种有限元单元板模型的平均应力-平均应变曲线Fig.5 Average stress-average strain curves of two kinds of plates with different finite element types

设定如图6所示的4种蚀坑分布模型，模型1是蚀坑有规律分布的板，其他3种模型是蚀坑随机分布的板，其有限元计算模型见图7.4种蚀坑分布模型的腐蚀体积相同，蚀坑的直径d和深度h分别为30 mm和6 mm.其他参数的设定与第1.2节中的设定相同.

由图8可知，模型1～模型4的平均应力-平均应变曲线的变化趋势基本一致，尤其是在极限强度到达之前，曲线吻合得很好；极限强度计算结果分别为162、164、160、163 mPa，非常近似，表明蚀坑有规律分布的板和蚀坑随机分布的板的极限强度差别很小，因此在后续分析中可以采用较简单的蚀坑有规律分布的板模型.

图6　4种蚀坑分布几何模型Fig.6 Four geometric models for pit distribution

图7　4种蚀坑分布有限元模型Fig.7 Four finite element models for pit distribution

图8　4种蚀坑分布板模型的平均应力-平均应变曲线Fig.8 Average stress-average strain curves of four kinds of plate models with different pit distributions

1.5蚀坑深度对极限强度的影响

板厚是影响极限强度的主要因素，而蚀坑深度不同相当于板的有效厚度不同，本节分析当腐蚀体积相同时蚀坑深度对极限强度的影响.

图9为设定的4种模型，其有限元模型见图10，腐蚀体积设为ΔV/V0=6.03% ，蚀坑直径为30 mm，蚀坑的深度和面积如表2所示.其他参数的设定与第1.2节中的设定相同.

图11表明 4种蚀坑深度板模型的平均应力-平均应变曲线变化一致；表2显示其极限强度计算结果近似相等，即当腐蚀体积相同时，蚀坑深度对极限强度几乎没有影响.

图9　4种蚀坑深度几何模型Fig.9 Four geometric models with different pit depths

图10　4种蚀坑深度有限元模型Fig.10 Four finite element models with different pit depths

表2　4种模型的蚀坑深度、蚀坑面积以及极限强度Tab.2 Depths and area of the corrosion pits and ultimate strength for four kinds of plate models

图11　4种蚀坑深度板模型的平均应力-平均应变曲线Fig.11 Average stress-average strain curves of four kinds of plate models with different pit depths

2　点蚀损伤板极限强度折减因子影响因素分析

对于点蚀损伤板极限强度的计算，通常由极限强度折减因子乘以无腐蚀损伤板极限强度得到，因此在研究极限强度折减因子计算公式之前，先要对点蚀损伤板极限强度折减因子的影响因素进行分析.

2.1板的初始柔度对极限强度折减因子的影响

对于无腐蚀损伤板，板的柔度是影响极限强度的重要因素.本节讨论对于点蚀损伤板，在基于腐蚀体积的极限强度折减因子计算中，板的初始柔度的影响.

船体板格结构的柔度通常为1.5～3.5［16］，而柔度越大的板，其极限强度越低，越容易发生破坏.据此，本节设定板的初始柔度分别为β0=1.83、1.96、2.26、2.44、2.67、2.93、3.26和3.67.板的初始厚度t0由板的初始柔度计算得到，其他参数的设定与第1.2节中的设定相同.

图12　具有不同初始柔度的腐蚀损伤板的极限强度折减因子与板的腐蚀体积的关系Fig.12 Relationship between ultimate strength reduction factor and corroded volume loss of pitted plates with different initial plate slendernesses

从图12可以看出（图中：σu为腐蚀损伤板极限强度；σu0为无腐蚀损伤板极限强度），不同初始柔度的腐蚀损伤板的极限强度折减因子与板的腐蚀体积间具有相同的变化规律，可用同一函数表示，即当腐蚀体积相同时板的初始柔度对极限强度折减因子的影响很小，在分析极限强度折减因子公式时可以忽略.

2.2板的初始变形对极限强度折减因子的影响

船体板的初始变形较难精确地测定，本文仅分析初始变形的最大幅值对极限强度折减因子的影响，而初始变形的形态假定均为线弹性第1阶屈曲模态.

根据第2.1节中分析，板的初始柔度为1.83～3.67，相应的板的初始厚度为16～8 mm.JSQS （Japanese ship quality standard）规定船体结构中允许的初始变形的最大幅值的上限是6 mm.DNV（det norske veritas）规范［17］规定板的初始变形的最大幅值为板宽度的1% .文献［18］表明船体板格初始变形的最大幅值从轻到重可分为0.025 β02t0、0.100 β02t0以及0.300 β02t03个程度.因此，本文设定板的初始变形的最大幅值为0.025 β02t0～0.100 β02t0.

设定模型长a=750 mm，初始厚度t0=12 mm，腐蚀体积ΔV/V0=12.31% ，其他参数的设定与第1.1节中的设定相同.当初始变形最大幅值分别为0.025 β02t0、0.050 β02t0、0.075 β02t0和0.100 β02t0时，计算得到的极限强度折减因子分别为0.822、0.825、0.829和0.831，表明板极限强度折减因子随板初始变形最大幅值的增加而有所增大，但在整个幅值的变化范围内，板极限强度折减因子增大得较小，对板极限强度的影响亦较小，在工程分析中可以忽略，本文分析暂不考虑.

2.3板的长宽比对极限强度折减因子的影响

通过对常见船型船体板格的调查，得出船体板格的长宽比在1.0～6.0之间，本节分析在此长宽比范围内，当腐蚀体积相同时极限强度折减因子的变化规律.

设定3组模型，腐蚀体积分别为2.26% 、4.02% 和9.04% ，每组模型只变化长宽比，其他相关参数与第1.1节中的设定相同.

图13表明板的长宽比对板的极限强度折减因子有所影响.当腐蚀体积不变时，板的长宽比与极限强度折减因子的关系可用抛物线表示，即

图13　板的长宽比与极限强度折减因子的关系Fig.13 Relationship between plate aspect ratio and ultimate strength reduction factor

式中：α 为板的长宽比；c为常数，当图13中腐蚀体积为4.02% 时，c=0.839，当腐蚀体积改变时，只需将抛物线上移或下移一定值，即只需改变c.

在应用时可计算某腐蚀体积下，当α=1.0时板的极限强度，然后根据式（2）计算相应的常数c.

2.4 板边缘线性载荷因子对极限强度折减因子的影响

通常认为，在计算船体板格极限强度时，板格边缘的载荷可以等效为线性载荷形式，即定义板边缘线性载荷因子ψx为

式中σx1和σx2分别为板边缘最小、最大压缩应力.

根据板边缘的受力情况，ψx的取值在-1.0～1.0变化.当ψx=-1.0时，载荷为纯弯曲形式；当ψx=1.0时，载荷为均匀压缩形式.本节在计算中取ψx分别为-1.00、-0.75、-0.50、-0.25、0、0.25、0.50、0.75、1.00，腐蚀体积均取为ΔV/V0=9.04% ，其他相关参数与第1.1节中的设定相同.

表3中的数据表明，当腐蚀体积相同时，板边缘线性载荷因子对板极限强度折减因子无影响，下文计算中ψx的值均取为1.0.

表3　不同板边缘线性载荷因子的腐蚀损伤板的极限强度折减因子Tab.3 Ultimate strength reduction factor of pitted plates with different linear load factors at plate edges

3　点蚀损伤板极限强度折减因子计算公式

对于存在点蚀损伤的板格，其极限强度的计算具有高度的非线性，很难用解析方法求得精确解.本节将在上文分析的基础上，通过有限元计算的数据，拟合出点蚀损伤板极限强度折减因子与主要影响因素的表达式，以便用于工程分析.

由第2节的分析结果可以看出，板的腐蚀体积（ΔV/V0）是影响点蚀损伤板极限强度的最主要因素.另外，板的长宽比α也对板极限强度折减因子有影响，其影响规律可用式（2）表示，具体计算方法见第2.3节.

在此基础上，首先，本文在第1.1节参数的基础上，设定长宽比α=1.0，变化板的腐蚀体积，计算板的极限强度折减因子，并得出板的极限强度折减因子与腐蚀体积的关系式.而第2.1节的分析计算数据即满足上述要求，参考图12，得到图中拟合曲线的计算式（4），其与有限元计算值的标准偏差为0.012，相关系数为0.989.图14显示了式（4）的计算值与有限元计算值的相对误差，仅有2个值在5% ～6% 之间，其余值均小于5% .图12及图14的结果表明式（4）可以满足工程分析的要求.

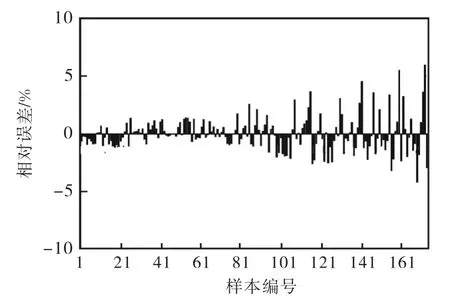
图14　式（4）的计算值与有限元计算值的相对误差Fig.14 Relative error between Eq.（4）and finite element analysis

然后按照式（2）及第2.3节的说明，对于不同板长宽比的情况进行修正，即可得到最终的点蚀损伤板的极限强度.

4　结 论

（1）在船体板格结构的腐蚀情况下，计算点蚀损伤板的极限强度，当板的腐蚀体积相同时，点蚀坑形状、有限元单元类型、蚀坑分布及蚀坑深度的影响均可忽略.

（2）对于船体板格结构，当板的腐蚀体积相同时，板初始柔度、板初始变形及板边缘线性载荷因子对极限强度折减因子的影响可以忽略.

（3）本文确立了基于腐蚀体积的点蚀损伤船体板格结构在单轴压缩下的极限强度折减因子的计算公式，并根据板的长宽比用相应的公式进行修正，此方法为服役期内点蚀损伤船体板格结构的安全评估提供了有效的技术支持.

参考文献：

［1］ Sadovský Z，Drdácký M. Buckling of plate strip subjected to localized corrosion——A stochastic model ［J］. Thin-Walled Structures，2001，39（3）：247-259.

［2］ Paik J K，Lee J M，Ko M J. Ultimate compressive strength of plate elements with pit corrosion wastage ［J］. J Engineering for the Maritime Environment，2003，217（M1）：185-200.

［3］ Dunbar T E，Pegg N，Taheri F，et al. A computational investigation of the effects of localized corrosion on plates and stiffened panels ［J］. Marine Structures，2004，17：385-402.

［4］ Nakai T，Matsushita H，Yamamoto N，et al. Effect of pitting corrosion on local strength of hold frames of bulk carriers（1st report）［J］. Marine Structures，2004，17：403-432.

［5］ 松下久雄，中井達郎，山本規雄，等. 船体構造部材の静的強度に及ぼす腐食の影響（第1報）［J］. 日本造船学会論文集，2002，192：357-365. Matsushita H，Nakai T，Yamamoto N，et al. Effect of corrosion on static strength of hull structural members（1st report）［J］. J Soc Naval Arch Jpn，2002，192：357-365（in Japanese）.

［6］ 中井達郎，松下久雄，山本規雄，等. 船体構造部材の静的強度に及ぼす腐食の影響（第2報）［J］. 日本造船学会論文集，2004，195：221-231. Nakai T，Matsushita H，Yamamoto N，et al. Effect of corrosion on static strength of hull structural members（2nd report）［J］. J Soc Naval Arch Jpn，2004，195：221-231（in Japanese）.

［7］ Ok D，Pu Yongchang，Incecik A. Computation of ultimate strength of locally corroded unstiffened plates under uniaxial compression ［J］. Marine Structures，2007，20：100-114.

［8］ Ok D，Pu Yongchang，Incecik A. Artificial neural networks and their application to assessment of ultimate strength of plates with pitting corrosion ［J］. Ocean Engineering，2007，34：2222-2230.

［9］ 江晓俐，Soares C G. 在面内压力作用下点腐蚀低碳钢板的非线性有限元分析［J］. 船舶力学，2009，13（3）：398-405. Jiang Xiaoli，Soares C G. Nonlinear FEM analysis of pitted mild steel square plate subjected to in-plane compression ［J］. Journal of Ship Mechanics，2009，13（3）：398-405（in Chinese）.

［10］ 江晓俐，吴卫国，梁志勇，等. 点腐蚀作用下非穿透低碳钢板的极限抗压承载能力数值分析［J］. 武汉理工大学学报：交通科学与工程版，2009，33（6）：1167-1170. Jiang Xiaoli，Wu Weiguo，Liang Zhiyong，et al. Ultimate compressive capacity analysis of pitted non-through mild steel plates ［J］. Journal of Wuhan University of Technology：Transportation Science & Engineering，2009，33（6）：1167-1170（in Chinese）.

［11］ Daidola J C，Parente J，Orisamolu I R，et al. Residual Strength Assessment of Pitted Plate Panels ［M］. Washington DC：Ship Structure Committee，1997.

［12］ Zhang Yan，Huang Yi，Liu Gang. A study on assessment of ultimate strength of ship structural plate with pitting corrosion damnification ［C］//Proceedings of the 8th（2008）ISOPE Pacific/Asia Offshore Mechanics Symposium. Bangkok：International Society of Offshore and Polar Engineers，2008：159-163.

［13］ Huang Yi，Zhang Yan，Liu Gang，et al. Ultimate strength assessment of hull structural plate with pitting corrosion damnification under biaxial compression ［J］. Ocean Engineering，2010，37：1503-1512.

［14］ Ueda Y，Yao T. The influence of complex initial deflection on the behaviour and ultimate strength of rectangular plates in compression ［J］. J Const Steel Res，1985，5：265-302.

［15］ Faulkner D. Effects of residual stresses on the ductile strength of plane welded grillages and of ring stiffened cylinders ［J］. The Journal of Strain Analysis for Engineering Design，1977，12（2）：130-139.

［16］ Paik J K，Thayamballi A K. Ultimate Limit State Design of Steel-Plated Structures ［M］. Chichester：John Wiley，2003.

［17］ Det Norske Veritas Classification. Buckling Strength Analysis，No. 30. 1 ［R］. Norway：DNVC，1995.

［18］ Fujikubo M，Yao T，Khedmati M R，et al. Estimation of ultimate strength of continuous stiffened panel under combined transverse thrust and lateral pressure Part 1：Continuous plate ［J］. Marine Structures，2005，18：383-410.

（责任编辑：赵艳静）

Ultimate Strength of Ship Structural Plate with Pitting Corrosion Damnification Under Uniaxial Compression

Zhang Yan1，Huang Yi2
（1.School of Naval Architecture and Ocean Engineering，Harbin Institute of Technology at Weihai，Weihai 264209，China；2.School of Naval Architecture Engineering，Dalian University of Technology，Dalian 116024，China）

Abstract：To simply and accurately calculate the ultimate strength of ship structural plates with corrosion damnification during the service lives of ships，the corrosion volume loss was used as the most important assessment parameter of the plate with corrosion damnification.On the basis of the characteristics of the actual hull structural plates，the effects of some parameters（the shape of pits，the type of finite elements，the distribution of pits and the depth of pits）on the ultimate strength and the effects of some parameters（the initial slenderness，the initial geometric deflection and the aspect of plates and the linear load factors at the plate edges）on ultimate strength reduction factor were studied by the nonlinear finite element analyses.The ultimate strength reduction factor formulae based on the corrosion volume loss were obtained by regression analysis approach.The results show that most of the relative errors between the calculating value by the formulae and finite element analysis result are below 5% and only very few is 5% —6% .The formulae can be used in the safety assessment of ship structural plates with pitting corrosion damnification during their service lives.

Keywords：ultimate strength；pitting corrosion；corroded volume loss；ship hull plate；uniaxial compression

中图分类号：U661.43

文献标志码：A

文章编号：0493-2137（2016）04-0429-08

DOI:10.11784/tdxbz201505106

收稿日期：2015-05-27；修回日期：2015-09-08.

基金项目：国家自然科学基金资助项目（51409073）.

作者简介：张 岩（1980— ），女，博士，讲师，zhangyan@hitwh.edu.cn.

通讯作者：黄 一，huangyi@dlut.edu.cn.