含有直线裂纹的直角域中椭圆形夹杂对SH波的散射

丁晓浩，齐 辉，赵元博

（哈尔滨工程大学航天与建筑工程学院，哈尔滨 150001）



含有直线裂纹的直角域中椭圆形夹杂对SH波的散射

丁晓浩，齐 辉，赵元博

（哈尔滨工程大学航天与建筑工程学院，哈尔滨 150001）

摘要：利用Green函数法、复变函数法及保角映射技术研究了SH波作用下直角域中直线裂纹对椭圆形夹杂动应力集中系数的影响.采用保角映射法和镜像叠加原理构造了一个能自动满足直角平面两个直线边界应力自由边界条件的散射位移场，并取含有椭圆形夹杂的直角域中任意一点承受时间谐和的出平面线源载荷作用下的位移基本解作为适合的Green函数.利用裂纹“切割”技术构造直线裂纹，进而得出裂纹与椭圆形夹杂共存时的位移场和应力场.通过具体算例讨论了入射波数、裂纹角度、裂纹长度等因素对椭圆形夹杂周边动应力集中系数的影响.

关键词：直角域；椭圆形夹杂；直线裂纹；保角映射；动应力集中系数（DSCF）

网络出版时间：2015-09-01. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20150901.0942.006.html.

在天然介质和工程材料中不可避免地会存在各种缺陷，缺陷的存在必然会影响材料的力学性能，了解材料在存在缺陷情况下的力学性能是众多研究者感兴趣的课题之一.尤其在动态载荷（如弹性冲击波）作用下缺陷对材料或结构的力学性能产生的影响情况，如缺陷处产生的动应力集中可能使材料或结构到达极限荷载前便发生局部破坏，导致材料或结构整体失效，因此，研究动态载荷作用下存在缺陷的材料或结构的动力学性能具有重要的理论价值和工程意义.在SH波作用下材料或结构动态响应的研究是弹性波研究中较为简单和发展较为成熟的问题之一，因此，数十年来取得了大量有价值的研究成果［1-12］.但在已取得的成果中，对直角域［10］中含有椭圆形夹杂［2 7］及直线裂纹［7-11］问题的研究却鲜见报道.为此，本文采用Green函数法和复变函数法并利用保角映射、镜像叠加、裂纹切割等技术研究了直线裂纹存在时对直角域中椭圆形夹杂周边动应力集中分布的影响，并给出具体算例分析了裂纹长度、裂纹角度、入射波数、介质参数等参数对动应力集中系数的影响.

1　问题的表述

图1所示为含有任意位置直线裂纹和椭圆形夹杂的直角域模型.ΓH、ΓV分别为直角域的水平和竖直边界，CΓ为椭圆形夹杂和基体的边界，n为边界CΓ上任意点的法线方向，夹杂中心O距水平边界距离为h，距竖直边界的距离为d，介质Ⅰ和介质Ⅱ的剪切模量和质量密度分别为1μ、1ρ和2μ、2ρ.裂纹所在轴线与x轴夹角为β，与点O的距离为h1，裂纹起点距y′轴的距离为L1，裂纹长度为L，在点O建立存在以下关系的xOy和x′ Oy′坐标系.

图1　含任意位置直线裂纹及椭圆形夹杂的直角域模型Fig.1 Model of right-angle plane with arbitrary beeline crack and elliptic inclusion

2　Green函数

本文取直角域中任意点承受时间谐和的出平面线源荷载作用时，直角域中位移函数的基本解作为适合的Green函数.引入复变量，在复平面中，Green函数G（略去时间因子e-iωt）满足以下控制方程：

式中k=ω/cs为入射波数，其中ω为波函数圆频率，cs为介质的剪切波数，

在极坐标下式（1）对应的应力为

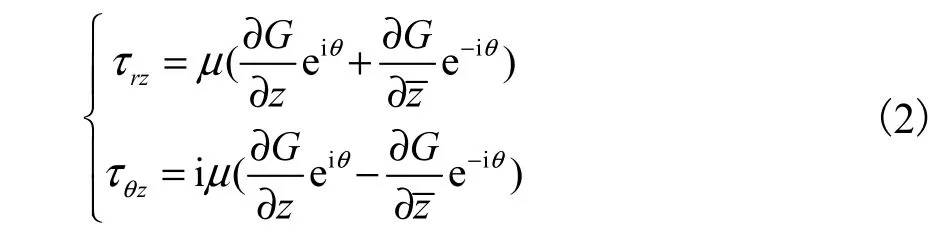
引入从复平面（z z）到复平面（ζ，ζ）的映射函数

式中：R=（ a+ b）/ 2，其中a、b为椭圆形夹杂半长轴和半短轴的长度；m=（ a + b）/（ a - b）.

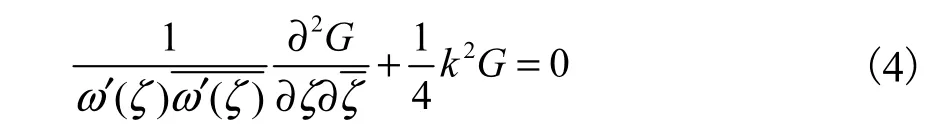
对应的应力公式（2）转变为

研究模型的边界条件可表述为

线源载荷δ（z- z0）在一个完整的直角域内的扰动可视为入射波G（i），本文研究的模型存在一个竖向直线边界，导致入射波在直线边界和夹杂间发生多次反射，使得求解满足自由表面上应力自由条件的波场存在困难.为了克服这一难题，利用“镜像法”将直角域沿边界ΓV镜像为半空间，并在镜像模型中引入复数坐标系z′= z +2 d ，如图2所示.且

图2　直角域模型镜像为半空间模型Fig.2 Transforming model from the right-angle to half plane

采用保角映射法将椭圆夹杂边界外域映射为单位圆外域后，可得到如下的入射波G（i）及反射波G（r）方程：

式中0ζ和0ζ′分别为线源荷载作用点z0和z0′在映射平面上的像.

直角平面中由椭圆形夹杂激发的散射波（s）G需满足直线边界处的应力自由条件，根据镜像叠加原理其应具有如下形式：

其中

式中：An为待求未知系数，可以由边界条件确定；为n阶的第一类Hankel函数.

在椭圆形弹性夹杂内激发的驻波具有以下形式：

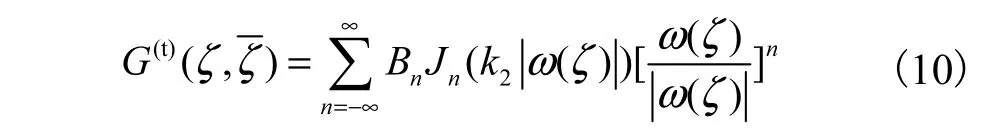
式中：Bn为待求未知系数，由边界条件确定；为n阶的第一类Bessel函数.

由边界条件（6）可以建立求解位置系数An和Bn的方程组，即

整理后得

其中

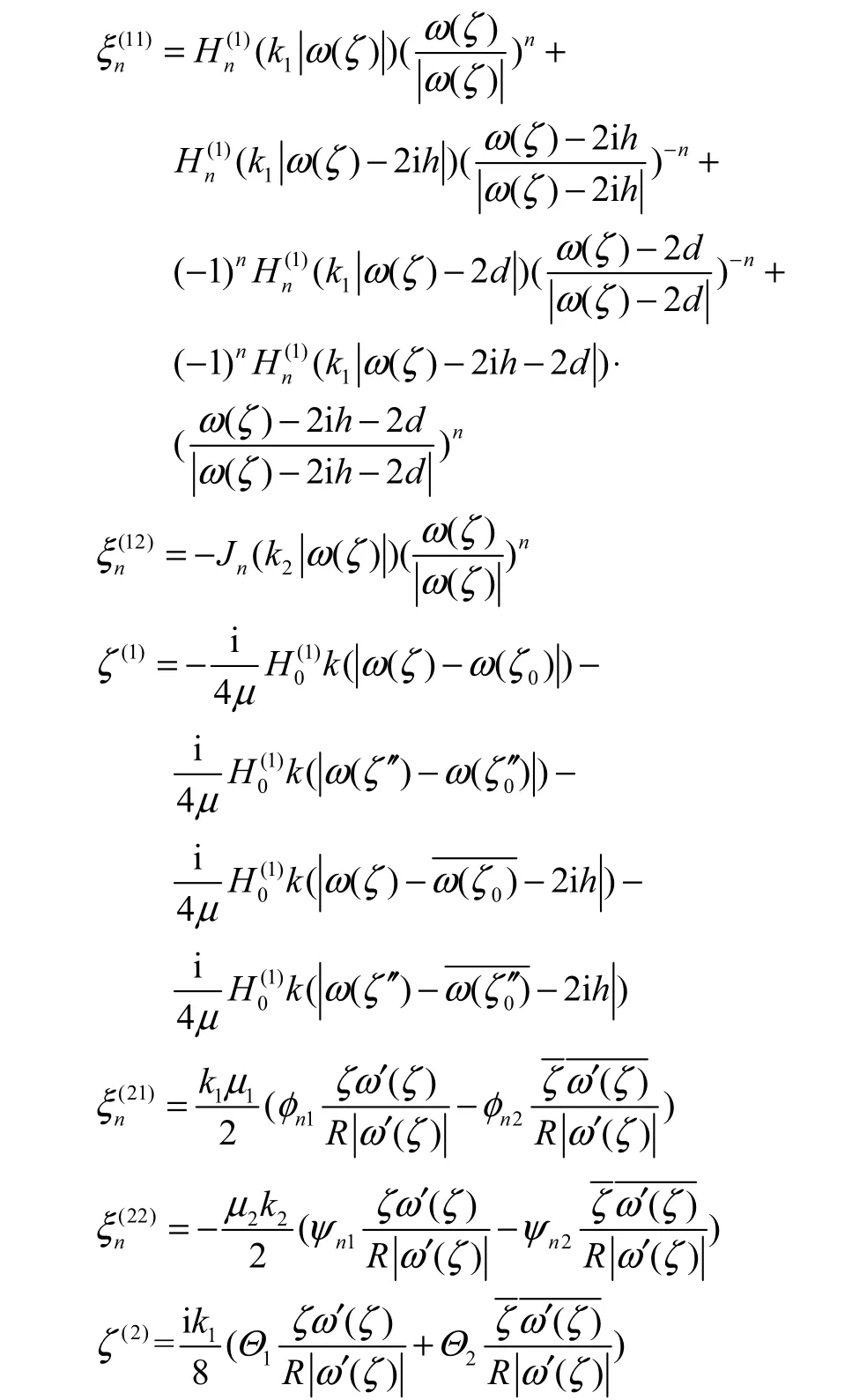
根据文献［8］中的方法，将具体表达式带入上述方程，在方程两边同乘exp（-im）θ，并在（-π π）上积分，通过有限项截断求解则可以求出An和Bn.

本文所用Green函数为

3　椭圆形夹杂对SH波的散射

与求解Green函数使用相同的思路，SH波入射完整直角域时，利用镜像叠加原理可以得出直角域内入射波场和反射波场，即

由椭圆形夹杂产生的散射波场与前文中构造Green函数时椭圆形夹杂的散射波场具有相同的形式，其中未知系数根据边界条件（6）确定，求解过程与求解Green函数的系数相同.

在仅含有椭圆形夹杂的直角域内利用裂纹“切割”［8-9］技术构造裂纹，即在欲出现裂纹的位置添加与此处切向应力zθτ大小相等、方向相反的平面载荷，使得此处的应力为零，从而构造出裂纹.此时附加的载荷作为新的波源对区域内的波场产生影响，则在椭圆形夹杂与裂纹共存的直角域中的波场可以表示为

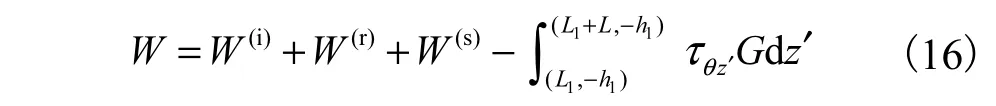
4　动应力集中系数

在SH波的作用下，夹杂周边动应力集中系数（DSCF）用符号可表示为以下形式：

其中

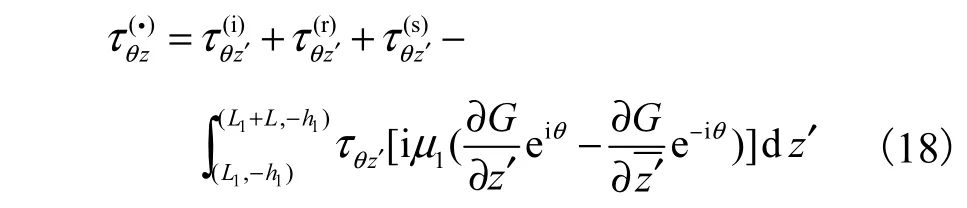
5　具体算例

本文以花岗岩中含有混凝土夹杂为例，给出SH波入射含有椭圆形夹杂和直线裂纹的直角域中时椭圆形夹杂周边环向动应力集中系数的分布情况.其中花岗岩与混凝土剪切模型之比，椭圆形夹杂的短长轴半长比b/ a= 0.8，夹杂的位置参数取d/ a = 12.0，h/ a=12.0，裂纹的方位角为β，入射波数用k1a表示，入射角用α0表示.

图3为取极端情况下椭圆形夹杂还原为圆形孔洞且裂纹长度为零时的圆形孔洞周边动应力集中系数分布情况，其结果与相同参数条件下文献［10-11］中所得结果一致，证明本文所用方法的可行性和准确性.

图4给出了SH分别以90°、45°入射时，椭圆形夹杂周边的动应力集中系数随入射波数变化的分布情况.由图4（a）可以看出，当SH波垂直入射到直角域时除准静态状态下，夹杂周边的随着入射波数的增大逐渐增大，最大值在高频入射时可达到5.69，约为半空间模型［7］中的2～3倍.对比图4（a）、（b）可以看出SH波垂直入射时的较倾斜入射时最大值4.76增大约24% ，说明入射波数和入射角度均对夹杂周边动应力集中系数有影响，且SH波以高频垂直入射时对地下结构的危害更大.

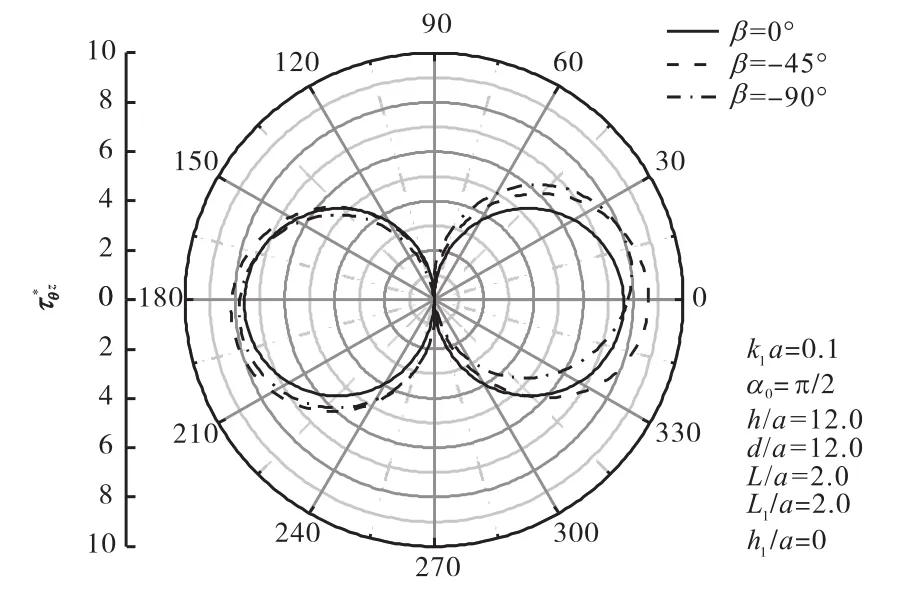
图3　SH波垂直入射时，随β 变化的分布情况Fig.3 Distribution ofwith β disturbed by incident SH-wave vertically

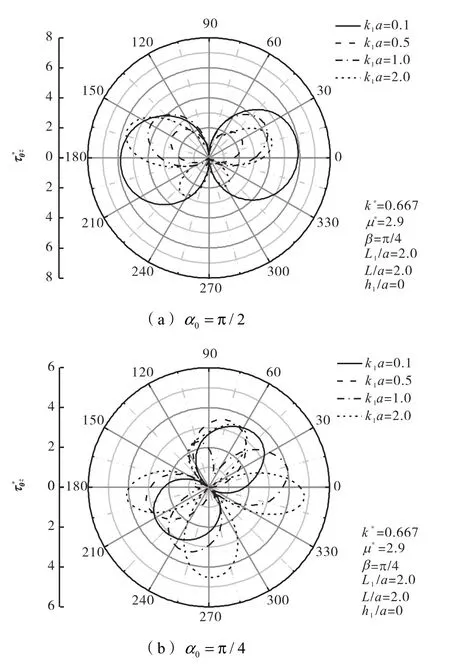
图4　随k1a变化的分布情况Fig.4 Distribution ofon the edge of inclusion with k1a

图5给出了裂纹处于不同方位时，SH波以90o入射时椭圆形夹杂动应力集中系数的分布情况.由图5可以看出，当SH波的入射方向与裂纹方向一致时，夹杂的分布情况与无裂纹时的分布基本重合，说明此时裂纹的存在对的影响可以忽略不计，当入射方向与裂纹方向垂直时，裂纹的存在对有明显的影响，说明裂纹方向对夹杂动应力集中系数的分布有影响.

图5　SH波垂直入射时夹杂周边随β变化的分布情况Fig.5 Distribution ofon the edge of the inclusion with β impacted by incident SH-wave vertically

图7给出了SH波以90°入射时夹杂边缘一点（θ=0°）的动应力集中系数随着裂纹距夹杂的距离h1/ a变化的分布情况.由图7（a）可以看出，当SH波以较低频率入射时，最大值发生在裂纹距离夹杂较近时，出现峰值后缓慢衰减，当h1/ a＞50时裂纹对其影响已经很小，最大值较不存在裂纹时提高了约7% .由图7（b）可看出，当SH波以较高频率入射时，距离h1/ a对值的影响呈现震荡衰减性，当h1/ a＞40时的变化曲线趋于稳定，说明此时裂纹对其影响已经很小，最大值提高了约25% .

图6　SH波垂直入射时夹杂周边随L/a变化的分布情况Fig.6 Distribution ofon the edge of the inclusion with L/a impacted by incident SH-wave vertically

图8给出了SH波以不同角度入射情况下，椭圆形夹杂边缘上一点（θ=0°）的动应力集中系数随着夹杂埋深h/ a的变化情况.由图8（a）可以看出，SH波垂直入射情况下当h/ a＞30后椭圆形夹杂的动应力集中系数分布趋于稳定，表明此时水平边界对其影响已经很小，可以忽略不计.当SH波倾斜入射时，h/ a＞50后的分布趋于稳定，表明此时水平边界对其影响已经很小， 可以忽略不计.说明椭圆形夹杂的埋深对其动应力集中系数有影响.

图7　夹杂边界上一点（θ=0°）的随h1/ a变化的分布情况Fig.7 Distribution ofat the point（θ=0°）on the edge of the inclusion with h1/ a

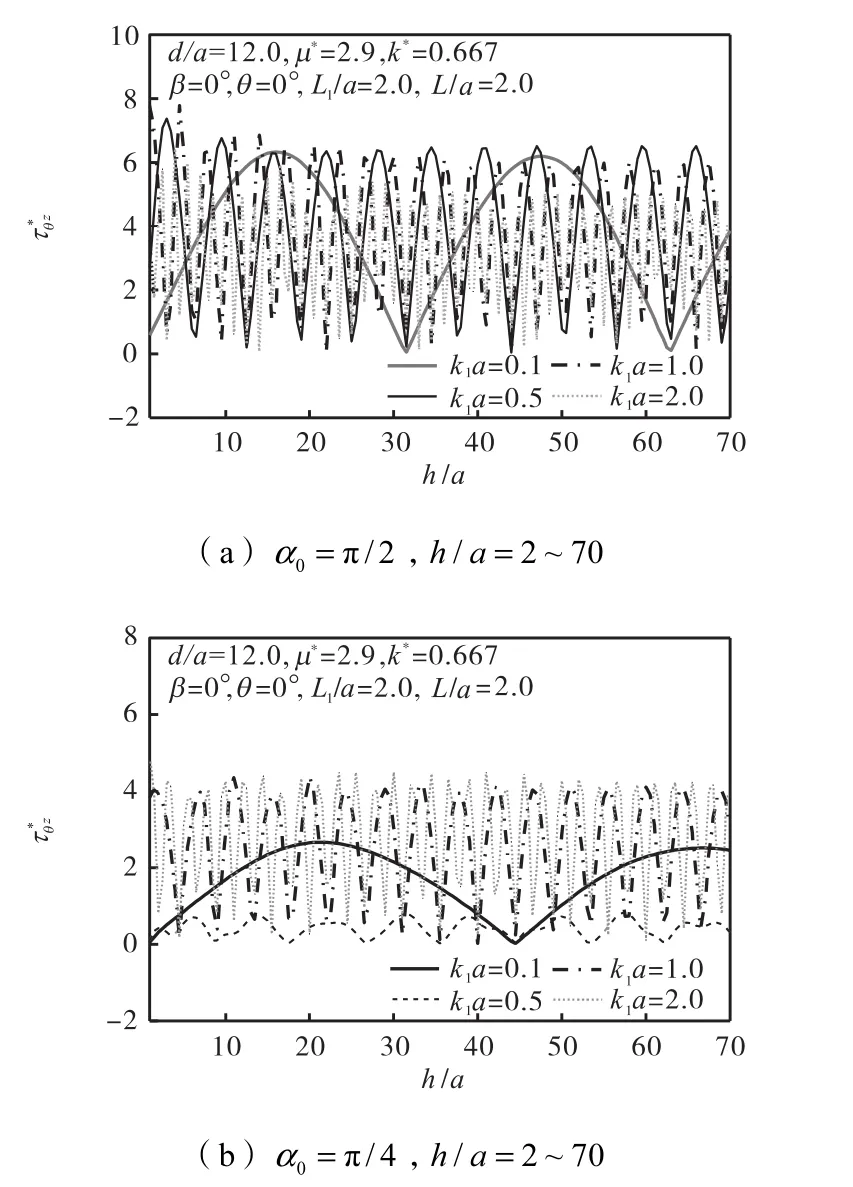
图8　夹杂边界上一点（θ=0°）随h/ a变化的分布情况Fig.8 Distribution ofat the point（θ=0°）on the edge of the inclusion with h/ a

6　结 语

本文采用Green函数法和复变函数法并结合“镜像”叠加原理、保角映射技术和裂纹“切割”技术研究了直角域中直线裂纹与椭圆形夹杂共存时夹杂周边动应力集中情况.通过算例，可以了解到裂纹对夹杂的动应力集中系数的影响不可以忽略，裂纹存在时的夹杂动应力集中系数较无裂纹时提高了约7% ～25% ，且在直角域中夹杂的动应力集中情况约为半空间中模型［10］的2～3倍.当SH波低频入射且h1/ a＞ 50时裂纹对夹杂边界点处的的影响可以忽略，当SH波以高频入射且h1/ a ＞40时，裂纹对夹杂边界点处的影响可以忽略.可以得出结论，直角域中椭圆形夹杂的动应力集中系数受到直线裂纹、自由边界、介质参数、入射波数等因素的影响.

参考文献：

［1］ Wong H L，Trifunac M D. Surface motion of a semielliptical alluvial valley for incident plane SH waves ［J］. Bulletin of the Seismological Society of America，1974，64（5）：1389-1403.

［2］ Lee V W，Amornwongpaibun A. Scattering of antiplane（SH）waves by a semi-elliptical hill：I-Shallow hill ［J］. Soil Dynamic and Earthquake Engineering，2012，52：116-125.

［3］ Luo Hao，Lee V W，Liang Jianwen. Antiplane（SH）waves diffraction by an underground semicircular cavity：Analytical solution ［J］. Earthquake Engineering and Engineering Vibration，2010，9（3）：385-396.

［4］ Hsu M-S，Tsaur D-H. Scattering of SH waves by a truncated semi-elliptic canyon ［J］. Journal of Mechanics，2014，30：137-144.

［5］ 韩 峰，王光政，陈 翰. SH波对多个凸起与凹陷相连地形的散射问题研究［J］. 应用数学和力学，2013，34（4）：355-363. Han Feng，Wang Guangzheng，Chen Han. Research on scattering of SH waves on multiple hills and canyons ［J］. Applied Mathematics and Mechanics，2013，34（4）：355-363（in Chinese）.

［6］ 梁建文，丁 美，杜金金. 柱面SH波在地下圆形衬

1砌洞室周围散射解析解［J］. 地震工程与工程振动，2013，33（1）：1-7. Liang Jianwen，Ding Mei，Du Jinjin. Diffraction of cylindrical SH waves around circular lined cavity：Analytical solution ［J］. Journal of Earthquake Engineering and Engineering Vibration，2013，33（1）：1-7（in Chinese）.

［7］ 杨在林，许华南，黑宝平. 半空间椭圆夹杂与裂纹对SH波的散射［J］. 振动与冲击，2013，32（11）：56-61. Yang Zailin，Xu Huanan，Hei Baoping. Interaction of elliptical and crack under incident SH-wave in a halfspace ［J］. Journal of Vibration and Shock，2013，32（11）：56-61（in Chinese）.

［8］ Qi Hui，Yang Jie. Dynamic analysis for circular inclusion of arbitrary positions near interfacial crack impacted by SH-wave in half-space ［J］. European Journal of Mechanics-A/Solids，2012，36：18-24.

［9］ 杨在林，闫培雷，刘殿魁. SH波对浅埋弹性圆柱及裂纹的散射与地震动［J］. 力学学报，2009，41（2）：229-235. Yang Zailin，Yan Peilei，Liu Diankui. Scattering of SH-waves and ground motion by an elastic cylindrical inclusion and a crack in half space ［J］. Chinese Journal of Theoretical and Applied Mechanics，2009，41（2）：229-235（in Chinese）.

［10］ 齐 辉，杨 杰，李宏亮，等. 含任意直线型裂纹的直角域中圆柱夹杂对SH波的散射［J］. 振动与冲击，2011，30（5）：208-212. Qi Hui，Yang Jie，Li Hongliang，et al. Scattering of SH-wave by a cylindrical inclusion in right-angle plane with arbitrary beeline crack ［J］. Journal of Vibration and Shock，2011，30（5）：208-212（in Chinese）.

［11］ Qi Hui，Shi Yong，Liu Diankui. Interaction of a circular cavity and a beeline crack in right-angle plane impacted by SH-wave ［J］. Journal of Harbin Institute of Technology：New Series，2009，16（4）：548-553.

［12］ 刘中宪，梁建文. 楔形空间中圆弧形沉积对平面SH波的散射解析解［J］. 天津大学学报，2010，43（7）：573-582. Liu Zhongxian，Liang Jianwen. Analytic solution for diffraction of plane SH waves by a circular alluvial valley in wedge-shaped space ［J］. Journal of Tianjin University，2010，43（7）：573-582（in Chinese）.

（责任编辑：赵艳静）

Scattering of SH-Wave by Elliptic Inclusion in Right-Angle Plane with Beeline Crack

Ding Xiaohao，Qi Hui，Zhao Yuanbo
（College of Aerospace and Civil Engineering，Harbin Engineering University，Harbin 150001，China）

Abstract：The scattering problem of SH-wave by elliptic inclusion in right-angle plane with an arbitrary beeline crack was analyzed by Green’s function，complex function method and conformal mapping method.The conformal mapping method and image method were employed to construct the scattering wave function，which satisfies the condition that stress is free on the straight boundaries of the right angle planes.An essential solution to the displacement field of an elastic right-angle plane containing an elliptic inclusion，whose any point bore an anti-plane harmonic line source load，was taken as Green’s function.The beeline crack was constructed with crack-division technique，and the expressions of displacement and stress fields were given when crack and elliptic inclusion co-exist.The dynamic stress concentration factor（DSCF）on the edge of elliptic inclusion was given and the influences of incident wave number，crack angle，crack length and other parameters on DSCF of elliptic inclusion were discussed.

Keywords：right-angle plane；elliptic inclusion；beeline crack；conformal mapping；dynamic stress concentration factor（DSCF）

中图分类号：O343.1；P315.3

文献标志码：A

文章编号：0493-2137（2016）04-0415-07

DOI:10.11784/tdxbz201504036

收稿日期：2015-04-10；修回日期：2015-07-20.

基金项目：黑龙江省自然科学基金资助项目（A201404）.

作者简介：丁晓浩（1989— ），男，博士研究生，dingxiaohao_2012@sina.cn.

通讯作者：齐 辉，qihui205@sina.com.