海洋环境要素综合影响下混凝土中氯离子的传输模型

练继建，张 杰，吴慕丹，王海军

（天津大学水利工程仿真与安全国家重点实验室，天津 300072）



海洋环境要素综合影响下混凝土中氯离子的传输模型

练继建，张 杰，吴慕丹，王海军

（天津大学水利工程仿真与安全国家重点实验室，天津 300072）

摘要：为澄清多种海洋环境要素对混凝土氯离子侵蚀的综合影响，在对混凝土氯离子侵蚀机理分析的基础上，建立了日照、潮汐、气温等海洋环境综合影响下的混凝土氯离子传输计算模型.该模型在传统对流-扩散模型中增加了ASHRAE晴空日照模型，并考虑了潮汐水位的周期变化导致的干湿两个过程中水分扩散以及水-土界面扩散等边界条件的差异，采取氯离子相对孔隙液的浓度作为控制指标，运用有限差分法，对海上混凝土结构全生命周期内的温度场、湿度场、氯离子浓度场进行动态耦合计算.通过试验实测数据对各模块计算结果进行验证，吻合良好.该模型对于海工混凝土的耐久性设计具有参考价值.

关键词：氯离子；耐久性；海洋环境；对流；扩散

氯离子侵蚀造成的海洋工程中混凝土结构耐久性破坏已成为一个日益突出的问题.当海水中的氯离子穿透混凝土保护层到达钢筋表面并逐渐积累至某临界浓度时，钢筋表面的钝化膜迅速破坏，钢筋开始锈蚀，造成钢筋体积膨胀，挤压混凝土保护层而出现裂缝甚至剥落，最终导致结构耐久性寿命的终结.关于这方面的研究，国内外学者已取得了许多成果［1-2］，多集中在实验室模拟环境下，针对某一特定因素进行研究.在模拟氯离子分布时，一般简化其为室温条件下的饱和混凝土，没有考虑温度和湿度的变化对氯离子传输的影响，其边界条件也往往采用一个由数据拟合的定值，没有针对其机理进行深入研究.

海上风电筒型基础［3-4］中的薄壁结构处于海洋潮汐区，不可避免地受到各种自然因素的共同作用，如太阳照射、潮汐、环境温度、空气湿度以及风速等.这些环境因素都直接或间接影响了氯离子的传输，在设计中应予以考虑.

本文的氯离子传输模型在对流-扩散传输模型基础上，代入了ASHRAE晴空日照模型，考虑了潮汐水位和环境气温、水温的周期变化，运用有限差分法，对海上风电混凝土基础结构全生命周期内的温度场、湿度场、氯离子浓度场进行动态耦合计算.

1　温度场计算

海上风电基础中处于海面上的结构表面不断地以辐射、对流和传导的方式与周围环境进行着热交换，表面与内部的温度都处于动态变化.温度场边界条件与所处的地理位置、地形地貌条件、方位朝向以及风速、气温、潮汐水位变化等因素有关，见图1.

图1　某海上风电基础的海洋环境要素Fig.1 Marine environment factors of an offshore wind power foundation

1.1太阳辐射强度计算

选择美国供暖、制冷和空气调节工程师协会推荐的ASHRAE晴空日照模型［5］，计算瞬时太阳辐射强度.该太阳辐射模型为晴空模型，是工程分析中所考虑的最不利天气条件，计算结果偏保守.建筑物吸收的太阳辐射由直射辐射GD、天空散射辐射和地面Gdθ与建筑物反射辐射GR组成，即

式中：γ为太阳辐射吸收率；GND为垂直入射直射太阳辐射强度，W/m2；θ为太阳入射角；Fws为表面对天空的角系数，（其中，α为计算表面与水平面之间的倾角）；Fwg为表面对地面的角系数，；ρg为地面或水面的反射率；C为水平面上的散射辐射与直射辐射的比值；β为太阳高度角，与纬度、日期、时刻以及平面方位和朝向有关，取值及计算方法见文献［6］.GND的表达式为

式中：A为大气层外的太阳辐射强度，W/m2；B为大气消光系数；CN为大气清洁度.

1.2对流换热计算

热对流是由于流体的宏观运动，各部分之间发生相对位移、冷热流体相互掺混所引起的热量传递，计算基础是牛顿冷却定律

式中：qh为热对流的热流密度；hc为对流换热系数；T为构件表面温度；T0为周围流体的温度.

考虑潮汐作用，当计算点位于水面以上时，为外界气温；当位于水面以下时，为海水温度，且认为此时hc很大.

1.3辐射换热计算

结构表面以电磁波形式向外界发射辐射，同时吸收来自周围环境发射的辐射.根据Stefan-Boltzmann定律，辐射热交换的热流密度qr为

式中：ε为表面辐射系数；Cs为Stefan-Boltzmann常数，其值为5.669×10-8W/m2；T*为绝对零度.

1.4热传导理论与边界条件

热传导为不同部位之间由于温度梯度而引起的内能交换.根据能量守恒，傅里叶热传导公式为

式中：k为混凝土的热传导系数，W/（m·℃）；ρ为材料密度，kg/m3；c为材料的比热容，J/（kg·℃）；t为时间；x为扩散深度.

当计算点位于水面以上时，结构表面暴露在大气中，结构表面和环境之间热量传递通过日照的qs、对流的qh、辐射的qr来实现，采用第3类边界

当计算点位于水面以下时，结构浸没在海水中，结构表面温度能迅速与水温平衡，边界条件近似为

2　湿度场计算

湿度在混凝土内的传输通量用孔隙饱和度的变化来表示，采用Fick定律的形式

式中：Jm为孔隙饱和度通量；ω为孔隙含水饱和度；Dw为湿度扩散系数.

2.1湿度扩散系数

为了区别湿度在干燥和湿润阶段扩散的差异，本模型分别采用了不同的湿度扩散系数.

湿润阶段（潮汐水面运动到计算高程以上）：

干燥阶段（潮汐水面运动到计算高程以下）：

式中：DS、D0为混凝土完全饱和与完全干燥时的扩散系数；ωc为扩散系数为DS/2时的孔隙饱和度；α0、n 和Bw为模型参数，采用CEB-FIP［7］推荐参数.

需要注意的是，在湿润阶段，仅在湿润前锋到达的范围内采用式（9），未到达的地方仍用式（10）.而在具体的数值计算中，在湿润阶段的每个时间步开始时，首先通过孔隙含水饱和度ω随深度变化的单调性来判断湿润前锋的位置，作为分界线.

Grace［8］发现温度对Dw影响很大，需根据上文得出的温度场对湿度扩散系数进行修正.在温度变化范围不大的情况下，采用Arrhenius经验公式表示温度活化过程，即

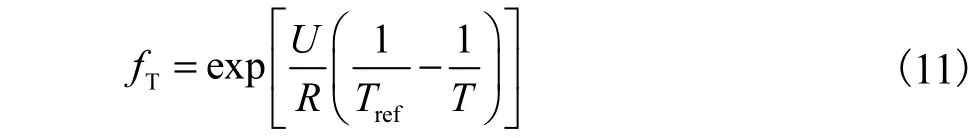
式中：fT为湿度传输的温度修正系数；U为湿度扩散过程活化能；R为摩尔气体常数，U/R取值［9］为2 500 k；Tref为热力学参考温度.

2.2湿度场计算边界条件

湿度场计算所采用的边界条件可分为两类：

（1）第1类边界条件（Dirichlet边界）

（2）第3类边界条件

式中：ωs为结构表面的饱和度；ωe为周围环境的等效饱和度；f为表面因子.

考虑潮汐作用下的干湿两种情况，湿润时的水分扩散系数相对干燥大很多，故湿润阶段采用第1类边界条件，ωe=1；干燥阶段采用第3类边界条件.王建等［10］指出当水灰比大于0.3时，考虑风速的影响，表面因子f为

式中：f0为风速为0时的表面因子，cm/d；wc为水灰比；v为计算高程处的平均风速.

该模型中湿度场的变量指标是孔隙含水饱和度，而空气用相对湿度表示.由于混凝土孔径小，难以测得负压，则使用等温吸附曲线，建立混凝土中水分含量与相对湿度的关系曲线.孙金阳［11］根据实验数据拟合得

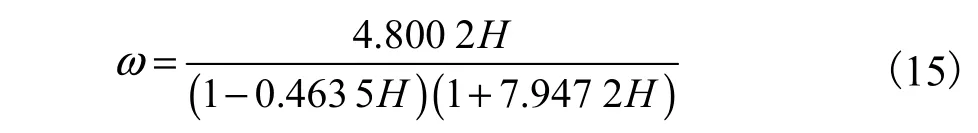
3　氯离子浓度计算

3.1氯离子传输控制方程

海上风电的薄壁混凝土基础中的氯离子主要以扩散和对流两种机制传输.氯离子从高浓度向低浓度处迁移，为扩散效应，见图2（a）；水分在混凝土中传输时，携带溶解于其中的离子一起运动，为对流效应，见图2（b）.氯离子的传输通量为

式中：Ccl为孔隙液中氯离子浓度；Dcl为氯离子扩散系数；φ 为混凝土孔隙率.

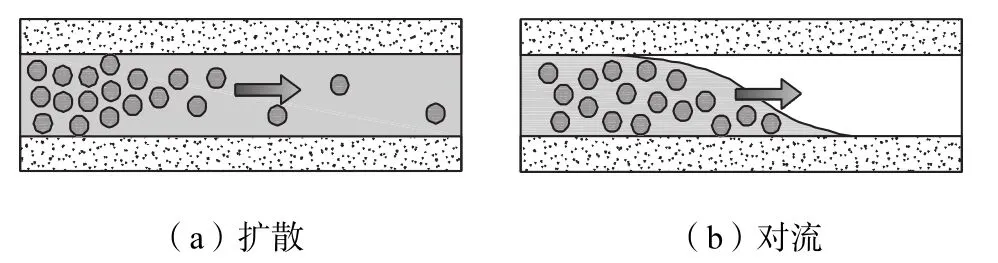
图2　对流-扩散机理示意Fig.2 Schematic illustration of convection-diffusion

式（16）中，氯离子浓度的变量指标采用氯离子相对孔隙液体积（质量）比，更符合实际扩散机理与锈蚀判定准则.因氯离子的扩散发生在混凝土孔隙液中，由高浓度处向低浓度处扩散.在潮汐的作用下，孔隙饱和度不断变化.尤其是在干燥阶段，表层水分蒸发，但氯离子滞留，浅层的孔隙液浓缩而成更高浓度氯离子溶液.在浓度梯度作用下，氯离子可继续向内部扩散.而传统的氯离子扩散模型中，受到实验测量方法的限制，通常采用氯离子相对混凝土质量比作为浓度指标，该指标无法体现孔隙饱和度变化对扩散的影响.此外判定钢筋开始锈蚀是以钢筋周围孔隙液的pH值作为临界值，取决于溶液中氯离子的含量，与混凝土固相无关.

3.2氯离子扩散系数

Saetta等［12］指出氯离子扩散系数可表示为

式中：Dc ref为参考龄期、温度下饱和混凝土中的氯离子扩散系数，使用Life-365［13］程序中采用的在20 ℃条件下养护28天混凝土的扩散系数与水灰比的关系来计算，D0=10-12.06+2.4 Wc；f1（T）、f2（ω）、f3（t）分别为温度、湿度、龄期对氯离子扩散的影响系数，其表达式为

式中：Tref为热力学参考温度，取293 k；Uc为扩散过程的活化能［12］（水灰比0.4时，Uc=49 887 J/mol；水灰比0.5时，Uc=45 314 J/mol）；R=8.315 J/（mol·K）；ωc为扩散系数衰减为一半时的混凝土中水分饱和度，取0.75；m为龄期衰减指数，与水灰比有关，m= 3（0.55-wc）.龄期衰减公式适用于前10 a，10 a后氯离子扩散系数将达到稳定.

3.3氯离子浓度计算边界条件

受潮汐的影响，氯离子浓度场计算的边界条件也需要分干燥与湿润两种情况.当潮汐水位活动到计算点以下时，混凝土处于大气环境中，水分能够在表面交换而离子不能，混凝土中的氯离子质量守恒：当潮汐水位活动到计算点以上时，混凝土浸没于海水中，水分和离子均可自由进出界面.

因混凝土表面与海水大面积接触，且海水处于流动状态（见图3），表层孔隙内积聚的高浓度氯离子能够以很快的速率扩散到海水中.引入一个扩散表面因数b，表征水土交界面氯离子扩散系数与内部扩散系数的倍数.

式中：C0为混凝土表层的氯离子浓度；Csea为海水中氯离子浓度；Dcs为饱和混凝土中的氯离子扩散系数.

图3　氯离子扩散截面示意Fig.3 Schematic of section of chlorideion diffusion

4　模型计算方法与验证

4.1多场耦合计算流程

基于前文所述的传输机理，建立数学模型.计算模型为高度非线性偏微分方程，采用有限差分法在空间域和时间域进行离散，计算流程见图4.

图4　模型计算流程Fig.4 Calculation flow chart of the model

4.2模块试验验证

4.2.1日照桥梁温度场实测

对于日照作用下的混凝土温度场，图5为某大跨箱梁的跨中截面的温度实测值与计算结果对比［14］.

大桥地理纬度为32.5°N；环境气温变化范围为21.1～34.5 ℃；混凝土的导热系数、比热容和密度分别为2.5 W/（m·K）、880 J/（kg·K）和2 400 kg/m3；大桥中轴线为南偏西41°；地表反射率为0.1.

从结果中提取日序227的顶板表面和东侧腹板表面温度，计算结果与实测温度变化趋势相同，吻合较好.东侧腹板表面的实测温度相比计算结果更“高瘦”，可能因侧面受水平风速影响较小，减慢了与外界空气的热传递，在日照作用下温度变化更为剧烈.

图5　大桥表面实测温度与计算结果对比Fig.5 Comparison of temperature of bridge surface between test and calculated results

4.2.2水下区浸泡实验

对于扩散模型，选定王传坤等［15］的室内浸泡试验. 混凝土试块边长为100 mm，水灰比为0.4.浸泡于浓度为15% 的NaCl溶液中，温度控制在30 ℃左右，35 d后取出试块，然后使用RCT对粉样进行氯离子测试.试验数据与模拟结果（见图6）非常吻合，充分说明本模型中的扩散模块已非常成熟.

图6　水下区的氯离子质量分数对比Fig.6 Comparison of mass fraction of chloride ion in under-water area

4.2.3干湿循环试验

Hong等［16］制作了水灰比为0.4的混凝土柱体.经23 ℃恒温养护28 d后，将试件6 h盐水浸泡（NaCl浓度为1 mol/L），18 h空气干燥（相对湿度为50% ），周期24 h的干湿循环条件，模拟多伦多大桥面板的除冰盐环境.试验分6组，分别在1 d、4 d、9 d、16 d、25 d、36 d后，绘制氯离子浓度曲线，如图7所示，与本模型计算结果吻合良好，同时拟合出表面因数在100左右.验证了本模型对干湿交替作用下氯离子传输机理分析的正确性.

图7　干湿循环条件下氯离子质量分数分布Fig.7 Distribution of mass fraction of chlorideion after cycles of wetting and drying

5　计算实例

应用本文模型，计算位于东海海域（地理纬度为31.8°N）的海上风电基础混凝土薄壁结构的氯离子浓度分布.不考虑混凝土初始带入的氯离子，且认为养护完成后混凝土是饱水的，各处温度相同.初始条件定为：C=0，ω=1，T=10 ℃.

5.1材料参数的取值

混凝土水灰比为0.30，孔隙率为13.8% ，密度为2 572 kg/m3，保护层素混凝土密度为2 274 kg/m3，比热容为840 J/kg·K，导热系数为1.74 W/m·K，混凝土表面的太阳辐射吸收率为0.65，辐射系数取3.34.其他计算参数见表1.

表1　CEB FIP model code推荐参数Tab.1 Parameters recommended by CEB FIP model code

刘玉等［17］应用扫描微参比电极法，模拟混凝土孔隙液中钢筋发生点腐蚀的氯离子浓度，得出氯离子临界浓度为0.04～0.05 mol/L.

5.2环境参数的取值

选取计算范围为200 mm，高程为海平面上1 m，方向朝南，计算风速为4 m/s，对流换热系数为16 W/（m2·K），海面反射率为0.35.海水中氯离子浓度为20 g/L（17%）；大气平均相对湿度为70% .平均日温差为10 ℃，15:00时达到峰值，气温变化用正弦曲线表示，海水水温取当日平均气温，即

式中：Ta为当月平均气温，1～12月的Ta分别为3.4、3.1、9.7、15.3、20.5、24.3、28.2、27.5、23.4、18.7、11.4、7.6 ℃；Tc为日温差.

以吴淞地区潮汐水位变化资料计算，潮差为3.50 m，线性插值表示如图8所示.

图8　吴淞地区潮汐水位变化Fig.8 Variations of tide level in Woosung area

5.3结果与分析

5.3.1温度场分析

据图9、图10中的温度计算结果可知：①混凝土的平均温度高于环境气温.图9（a）中温度的大波动是由于每月的日照状况不同，小波动是由于每日的潮汐状况不同.②混凝土的内外温差达10 ℃以上，冬季的内外温差大于夏季.因冬季太阳高度角较小，对于竖直平面近乎垂直入射，故冬季太阳辐射对温度场的影响更大. ③表面温度的变化幅度大于内部温度，内部温度变化滞后于表面.④浸没时混凝土温度迅速向水温趋近.

图9　混凝土温度场年变化Fig.9 Annual variations of concrete temperature field

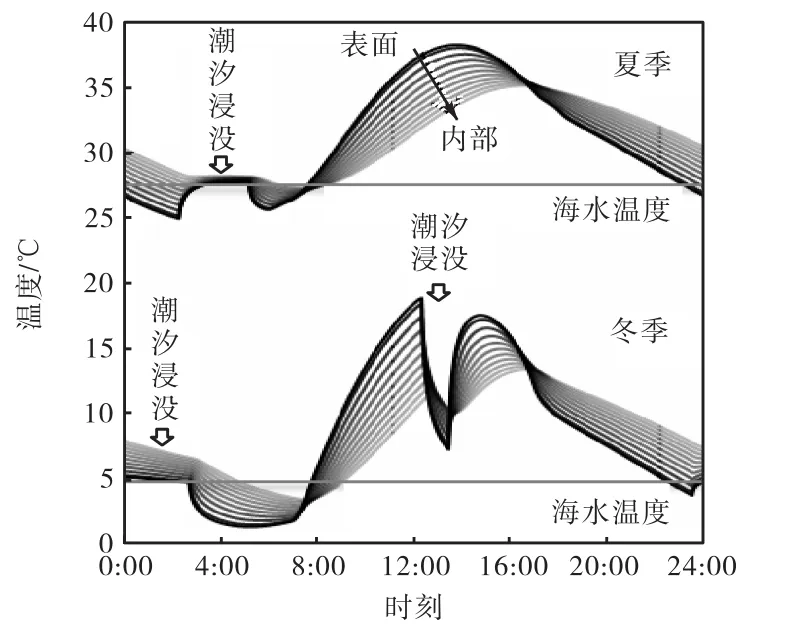
图10　混凝土温度场日变化Fig.10 Diurnal variations of concrete temperature field

5.3.2湿度场分析

湿润过程比干燥过程进行得更快，因为该模型分别采用了不同的湿度扩散系数，更符合真实情况.潮汐作用下，干湿循环对湿度场的最大影响深度约10 mm，见图11.在此范围内，对流效应为氯离子传输的主要机制.

图11　干燥和湿润过程的湿度场变化Fig.11 Humidity field change during wetting and drying processes

5.3.3氯离子浓度场分析

氯离子不断地向混凝土内部传输.在对流区内氯离子的浓度高于海水浓度.干湿交替作用下，干燥时水分向外蒸发而氯离子在表面积累；湿润时海水向内部渗透，将表面积累的氯离子运输到了对流区内部.对流效应在初期增长较为显著，后期对流与扩散达到平衡，对流区氯离子质量浓度趋于稳定.在距表面10 mm以外的混凝土始终处于饱和状态，氯离子以扩散的机制传输，见图12（a）.

图12（b）描绘了混凝土内5 mm、15 mm、25 mm深度处的氯离子质量浓度时程变化，分别代表了对流区、扩散区浅层、扩散区深层.各处的氯离子质量浓度都是波动变化的.在扩散区温度因素的影响下，夏季增速较快，冬季增速较慢.而在对流区却出现了相反的规律.由于对流区的浓度变化受表面输入和内部输出两方面因素影响，在二者之间达到平衡.表面边界条件变化不大，而内部扩散输出夏季多冬季少，故对流区出现氯离子增长夏季慢冬季快的现象.

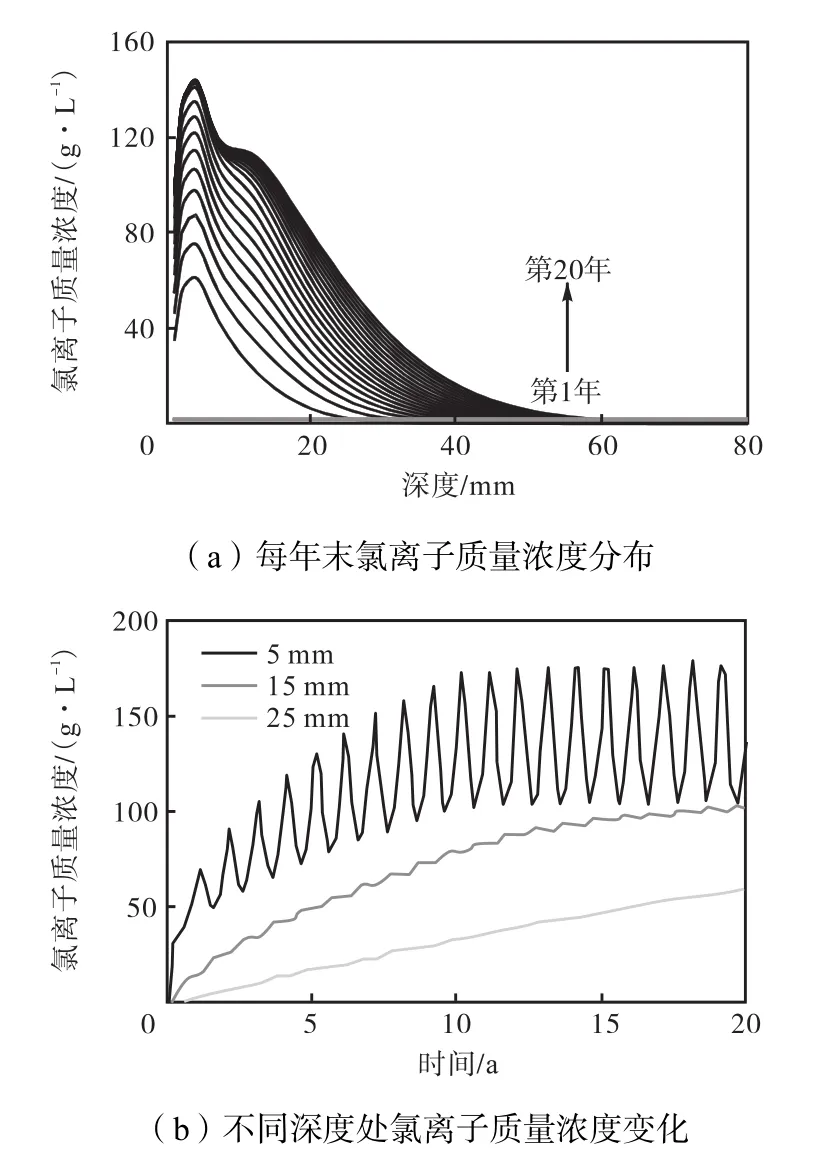
图12　混凝土氯离子浓度场模拟Fig.12 Simulation of chloride ion profiles in concrete

图13展示了服役20 a后混凝土的侵蚀状况，可看出朝南的氯离子侵蚀最深，朝北最浅，比其他方向浅3.9 mm.归因于在该地区的竖直平面，朝南面接受更多的日照，所以年平均温度更高，见图14.正因为本模型考虑了日照因素，故氯离子扩散系数在朝南方向上相对较大.

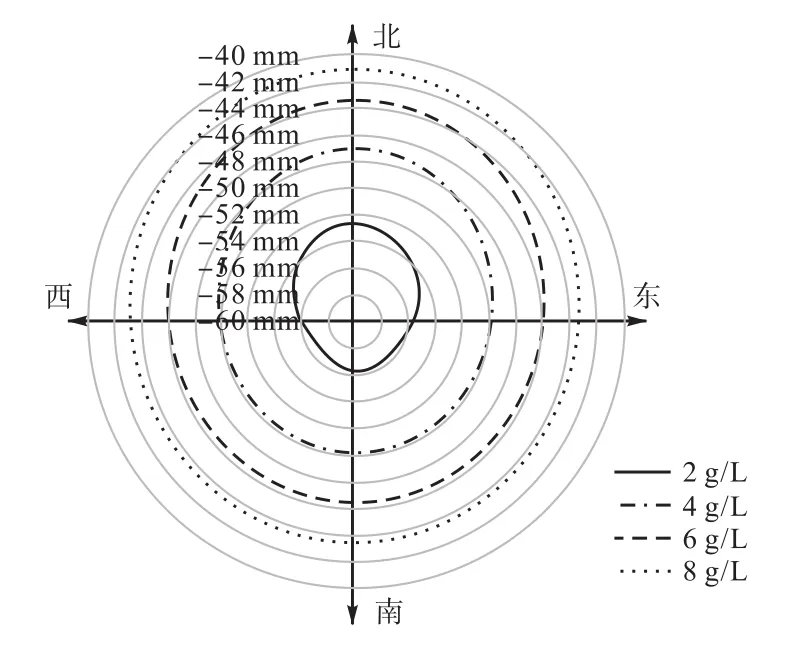
图13　20 a后的氯离子质量浓度等值线Fig.13 Contour of mass concentration of chloride ion after 20 a

图14　氯离子传输的温度因素Fig.14 Influence of temperature on chloride ion transport

6　结 论

（1）该地区年平均气温为16.1 ℃，在日照作用下，混凝土结构平均温度为19.7 ℃.表面温度年变化范围为0.5～38.2 ℃，内外最大温差可达10 ℃.

（2）潮汐作用下，混凝土表面10 mm深度范围内的湿度场受干湿影响，形成对流区；10 mm以上深度处混凝土保持饱和状态，为扩散区.

（3）氯离子呈冬夏快慢交替式传输，服役20 a后的氯离子侵蚀深度结果为：朝北52.2 mm，朝南56.1 mm.由于朝南全年日照辐射吸收量约为朝北的3倍，年平均温度高2.8 ℃，侵蚀深度大3.9 mm.

（4）结果表明，混凝土配合比、钢筋保护层厚度以及温度效应、干湿循环制度是影响混凝土耐久性寿命的主要因素.其中温度效应取决于环境温度和日照条件，包括纬度、倾角、朝向；干湿循环制度取决于潮汐变化规律和计算高程.该模型可应用于海工混凝土结构的耐久性设计中.

参考文献：

［1］ 李春秋，李克非. 干湿交替下表层混凝土中氯离子传输：原理、试验和模拟［J］. 硅酸盐学报，2010，38（4）：581-589. Li Chunqiu，Li Kefei. Chloride ion transport in cover concrete under drying-wetting cycles：Theory，experiment and modeling ［J］. Journal of the Chinese Ceramic Society，2010，38（4）：581-589（in Chinese）.

［2］ 刘春生，陈 雷，朱 涵. 氯盐侵蚀环境下橡胶集料掺量对钢筋混凝土梁耐久性的影响［J］. 天津大学学报，2011，44（1）：40-45. Liu Chunsheng，Chen Lei，Zhu Han. Influence of crumb rubber proportion on durability of reinforced concrete beams exposed to chloride aggressive environment ［J］. Journal of Tianjin University，2011，44（1）：40-45（in Chinese）.

［3］ 丁红岩，于 瑞，张浦阳，等. 海上风电大尺度预应力筒型基础结构预应力优化设计［J］. 天津大学学报，2012，45（6）：473-480. Ding Hongyan，Yu Rui，Zhang Puyang，et al. Optimal design for prestress of large-scale bucket foundation for offshore wind turbine［J］. Journal of Tianjin University，2012，45（6）：473-480（in Chinese）.

［4］ 刘 润，李宝仁，练继建，等. 海上风电单桩复合筒型基础桩筒共同承载机制研究［J］. 天津大学学报：自然科学与工程技术版，2015，48（5）：429-437. Liu Run，Li Baoren，Lian Jijian，et al. Bearing characteristics of pile-bucket composite foundation for offshore wind turbine［J］. Journal of Tianjin University：Science and Technology，2015，48（5）：429-437（in Chinese）.

［5］ 任志刚，胡曙光，丁庆军. 太阳辐射模型对钢管混凝土墩柱温度场的影响研究［J］. 工程力学，2010，27（4）：246-250，256. Ren Zhigang，Hu Shuguang，Ding Qingjun. Research on the effect of solar radiation model on temperature fieldof concrete-filled steel tube pier ［J］. Engineering Mechanics，2010，27（4）：246-250，256（in Chinese）.

［6］ 李锦萍，宋爱国. 北京晴天太阳辐射模型与ASHRAE模型的比较［J］. 首都师范大学学报：自然科学版，1998，19（1）：37-40. Li Jinping，Song Aiguo. Compare of clear-day solar radiation model of Beijing and ASHRAE［J］. Journal of Capital Normal University：Natural Science Edition，1998，19（1）：37-40（in Chinese）.

［7］ Comite Euro-International du Beton. CEB-FIP Model Code 1990［S］. London：Thomas Telford，1993：68-69.

［8］ Grace W R. Chloride penetration in marine concrete—A computer model for design and service life evaluation［J］. Corrosion，1991，47（32）：1-19.

［9］ Bazant Z P，Najjar L J. Nonlinear water diffusion in nonsaturated concrete［J］. Material and Structures，1972，5（1）：3-20.

［10］ 王 建，戴会超，顾冲时. 混凝土湿度运移数值计算综述［J］. 水力发电学报，2005，24（2）：85-89. Wang Jian，Dai Huichao，Gu Chongshi. Summary on numerical calculation of moisture transfer in concrete［J］. Journal of Hydroelectric Engineering，2005，24（2）：85-89（in Chinese）.

［11］ 孙金阳. 混凝土湿润与干燥过程中水分传输规律研究［D］. 杭州：浙江大学建筑工程学院，2012. Sun Jinyang. Research on Moisture Transport Under Wetting and Drying Conditions［D］. Hangzhou：School of Civil Engineering，Zhejiang University，2012（in Chinese）.

［12］ Saetta A V，Scotta R V，Vitaliani R V. Analysis of chloride diffusion into partially saturated concrete［J］. ACI Materials Journal，1993，90（5）：441-451.

［13］ Thomas M D A，Bentz E C. Life-365：Computer Program for Predicting the Service Life and Life-Cycle Costs of Reinforced Concrete Exposed to Chloride［M］. St Paul：Cortec Corporation，2001.

［14］ 张亮亮，赵艳青，杨 磊. 基于ANSYS的混凝土箱梁日照温度应力数值分析［J］. 计算机应用，2011，31（增1）：177-180. Zhang Liangliang，Zhao Yanqing，Yang Lei. Analysis of solar radiation thermal stress of concrete box girders based on ANSYS［J］. Journal of Computer Applications，2011，31（Suppl 1）：177-180（in Chinese）.

［15］ 王传坤，高祥杰，赵羽习，等. 混凝土表层氯离子含量峰值分布和对流区深度［J］. 硅酸盐通报，2010，29（2）：262-267. Wang Chuankun，Gao Xiangjie，Zhao Yuxi，et al. Peak value distribution of surface chloride concentration and convection depth of concrete［J］. Bulletin of the Chinese Ceramic Society，2010，29（2）：262-267（in Chinese）.

［16］ Hong K，Hooton R D. Effects of cyclic chloride exposure on penetration of concrete cover［J］. Cement and Concrete Research，1999，29（9）：1379-1386.

［17］ 刘 玉，杜荣归，李 彦，等. 模拟混凝土孔隙液中钢筋腐蚀的氯离子临界浓度测试［J］. 分析化学，2006，34（6）：825-828. Liu Yu，Du Ronggui，Li Yan，et al. Determination of the chloride threshold concentration for reinforcing steel corrosion initiation in simulated concrete pore solution［J］. Chinese Journal of Analytical Chemistry，2006，34（6）：825-828（in Chinese）.

（责任编辑：樊素英）

Chloride Ion Transport Model in Concrete Under Combined Influence of Marine Environment Factors

Lian Jijian，Zhang Jie，Wu Mudan，Wang Haijun
（State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China）

Abstract：In order to clarify the various marine environment factors that affect the chloride ion erosion，by means of analyzing chloride ion erosion mechanism in reinforced concrete，chloride ion transport calculation model under the marine environment including sunshine，tide and temperature was established. Based on the convection-diffusion transmission model，this model was applied to dynamically coupling calculation of temperature field，humidity field and chlorine ion concentration field in the whole life cycle of concrete structures using finite difference method. In the model，the ASHRAE model was plugged in，and the differences of moisture diffusion and physical field boundary conditions in dry-wet process caused by tidal water level cycles were considered. The ratio of chloride ion to pore fluid was taken as concentration index. The calculated results of every module were validated by test data，and showed good agreement. The model may provide valuable references for marine concrete durability design.

Keywords：chloride ion；durability；marine environment；convection；diffusion

中图分类号：TU528

文献标志码：A

文章编号：0493-2137（2016）04-0333-08

DOI:10.11784/tdxbz201410001

收稿日期：2014-10-04；修回日期：2014-12-19.

基金项目：国家创新研究群体科学基金资助项目（51021004）；国家国际科技合作专项资助项目（2012DFA70490）.

作者简介：练继建（1965— ），男，博士，教授，fj_np@126.com.

通讯作者：张 杰，zhangjiewow@hotmail.com.